Next: 4.9. Заключение
Up: 4. Алгоритмические проблемы теории
Previous: 4.7. Как раскладывают составные
Contents: Содержание
4.8. Дискретное логарифмирование
Пусть  - нечетное
простое число. Еще Эйлер знал, что мультипликативная группа
кольца
- нечетное
простое число. Еще Эйлер знал, что мультипликативная группа
кольца  циклична, т.е. существуют такие целые числа
циклична, т.е. существуют такие целые числа
 , что сравнение
, что сравнение
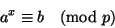 |
(22) |
разрешимо относительно

при любом

, не делящемся
на

. Числа

с этим свойством называются первообразными
корнями, и количество их равно

, где

-
функция Эйлера.
Целое  , удовлетворяющее сравнению (22
, удовлетворяющее сравнению (22),
называется индексом или дискретным логарифмом числа

.
В разделе 2 мы описали алгоритм, позволяющий по заданному
числу  достаточно быстро вычислять
достаточно быстро вычислять  . Обратная
же операция - вычисление по заданному
. Обратная
же операция - вычисление по заданному  его дискретного
логарифма, вообще говоря, является очень сложной в
вычислительном отношении задачей. Именно это свойство
дискретного логарифма и используется в его
многочисленных криптографических применениях (см. главу 1). Наиболее
быстрые (из известных) алгоритмы решения этой задачи, основанные на
так называемом методе решета числового поля, требуют выполнения
его дискретного
логарифма, вообще говоря, является очень сложной в
вычислительном отношении задачей. Именно это свойство
дискретного логарифма и используется в его
многочисленных криптографических применениях (см. главу 1). Наиболее
быстрые (из известных) алгоритмы решения этой задачи, основанные на
так называемом методе решета числового поля, требуют выполнения
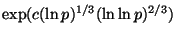 арифметических операций (см. [25]), где
арифметических операций (см. [25]), где 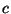 - некоторая
положительная постоянная. Это сравнимо со сложностью наиболее
быстрых алгоритмов разложения чисел на множители. Конечно,
указанная оценка сложности получена при условии
справедливости ряда достаточно правдоподобных гипотез.
- некоторая
положительная постоянная. Это сравнимо со сложностью наиболее
быстрых алгоритмов разложения чисел на множители. Конечно,
указанная оценка сложности получена при условии
справедливости ряда достаточно правдоподобных гипотез.
Говоря о сложности задачи дискретного логарифмирования, мы имели в
виду ``общий случай''. Ведь и большое целое число легко
может быть разложено на простые сомножители, если все эти
сомножители не очень велики. Известен алгоритм, позволяющий
быстро решать задачу дискретного логарифмирования, если  есть произведение малых простых чисел.
есть произведение малых простых чисел.
Пусть  - простое число, делящее
- простое число, делящее  . Обозначим
. Обозначим
 ,
тогда
классы вычетов
,
тогда
классы вычетов
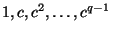 все различны и
образуют полное множество решений уравнения
все различны и
образуют полное множество решений уравнения 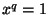 в поле
в поле
 .
Если
.
Если  не велико и целое число
не велико и целое число  удовлетворяет сравнению
удовлетворяет сравнению
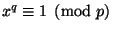 ,
то показатель
,
то показатель  ,
, 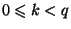 , для которого выполняется
, для которого выполняется
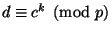 , легко
может быть найден, например, с помощью перебора. Именно на этом
свойстве основан упомянутый выше алгоритм.
, легко
может быть найден, например, с помощью перебора. Именно на этом
свойстве основан упомянутый выше алгоритм.
Допустим, что  ,
,  . Алгоритм последовательно
строит целые числа
. Алгоритм последовательно
строит целые числа  ,
,  , для которых
выполняется сравнение
, для которых
выполняется сравнение
 |
(23) |
Так как выполняется сравнение

,
то найдется целое число

, для
которого
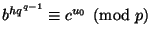
.
При таком выборе сравнение (
23) с
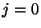
, очевидно,
выполняется. Предположим, что найдено число

,
удовлетворяющее сравнению (
23). Тогда определим

с помощью
сравнения
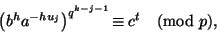 |
(24) |
и положим

. Имеют место сравнения
 |
(25) |
означающие справедливость (
23) при
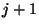
.
При 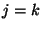 сравнение (23) означает в силу (22), что
сравнение (23) означает в силу (22), что
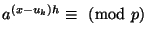 .
Целое число
.
Целое число  есть первообразный корень по модулю
есть первообразный корень по модулю  ,
поэтому имеем
,
поэтому имеем
 и
и

Если
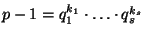 , где все простые числа
, где все простые числа
 малы, то указанная процедура позволяет найти вычеты
малы, то указанная процедура позволяет найти вычеты
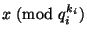 ,
, 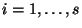 , и, с
помощью китайской теоремы об остатках, вычет
, и, с
помощью китайской теоремы об остатках, вычет
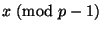 ,
т.е. решить
сравнение (22).
,
т.е. решить
сравнение (22).
В случае обычных логарифмов в поле действительных чисел имеется
специальное основание
 , позволяющее
достаточно быстро вычислять логарифмы с произвольной точностью.
Например, это можно делать с помощью быстро сходящегося ряда
, позволяющее
достаточно быстро вычислять логарифмы с произвольной точностью.
Например, это можно делать с помощью быстро сходящегося ряда
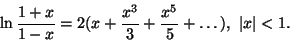 |
(26) |
Логарифмы по произвольному основанию

могут быть вычислены с помощью
тождества
 |
(27) |
В случае дискретных логарифмов нет основания, по которому логарифмы
вычислялись бы столь же быстро, как натуральные в поле действительных
чисел. Вместе с тем, последняя формула, связывающая логарифмы с
различными основаниями, остается справедливой и позволяет выбирать
основание удобным способом. Единственное условие для этого состоит в
том, чтобы логарифм нового основания
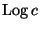
был взаимно прост с

. Тогда в формуле (
27) возможно деление по модулю

.
Заметим, что это условие будет выполнено, если и только если
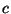
-
первообразный корень. Из расширенной гипотезы Римана следует, что
наименьший первообразный корень по модулю

ограничен величиной
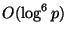
.
Поэтому в дальнейшем для простоты изложения мы будем
предполагать, что основание

в (
22) невелико, именно
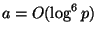
.
Так как поле  неполно, вычисление дискретных логарифмов
не может использовать предельный переход и основано на иных
принципах. Прежде всего, нужный дискретный логарифм
неполно, вычисление дискретных логарифмов
не может использовать предельный переход и основано на иных
принципах. Прежде всего, нужный дискретный логарифм 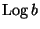 вычисляется не сам по себе, а вместе с совокупностью логарифмов
ряда других чисел. Заметим, что всякое сравнение вида
вычисляется не сам по себе, а вместе с совокупностью логарифмов
ряда других чисел. Заметим, что всякое сравнение вида
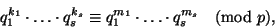 |
(28) |
где

, приводит к соотношению между
логарифмами
 |
(29) |
А если выполняются сравнения
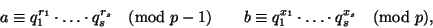
то
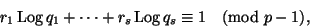 |
(30) |
и
 |
(31) |
Имея достаточно много векторов
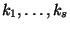
,

с условием (
28), можно
найти решение соответствующей системы сравнений (
29), (
30).
Если эта система имеет единственное решение, то им как раз и
будет набор логарифмов

.
Затем с помощью (
31) можно найти
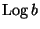
.
Мы опишем ниже реализацию этой идеи, взятую из работы [18].
Эвристические соображения позволили авторам [18] утверждать,
что предложенный ими алгоритм требует
 , где
, где
 ,
арифметических операций для вычисления
,
арифметических операций для вычисления 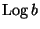 .
.
Положим
![\begin{displaymath}H=\left[\sqrt p\right]+1,\quad J=H^2-q.\end{displaymath}](img860.gif)
Тогда
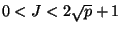
,
и, как легко проверить, для любой пары целых чисел

выполняется сравнение
 |
(32) |
Если числа

не очень велики, скажем

при некотором
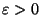
, то
правая часть сравнения (
32) не превосходит

. Можно доказать,
что случайно выбранное натуральное число
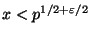
раскладывается в
произведение простых чисел, меньших
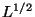
, с вероятностью
большей, чем
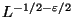
.
Обозначим через
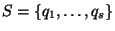 совокупность
всех простых чисел
совокупность
всех простых чисел
 , а также всех целых чисел вида
, а также всех целых чисел вида 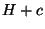 при
при
 .
Тогда
.
Тогда
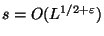 . Будем теперь перебирать случайным
образом числа и для каждой такой пары пытаться разложить
на множители соответствующее выражение из правой части (32).
Для разложения можно воспользоваться, например,
делением на все простые числа, меньшие чем
. Будем теперь перебирать случайным
образом числа и для каждой такой пары пытаться разложить
на множители соответствующее выражение из правой части (32).
Для разложения можно воспользоваться, например,
делением на все простые числа, меньшие чем 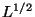 . Перебрав все
. Перебрав все
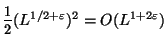 указанных пар
указанных пар  , мы найдем, как это следует из
указанных выше вероятностных соображений, не менее
, мы найдем, как это следует из
указанных выше вероятностных соображений, не менее
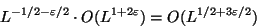 |
(33) |
пар, для которых правая часть сравнения (
32) полностью
раскладывается на простые сомножители, меньшие
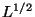
. Сравнение (
32), таким образом, принимает вид (
28).
Так строится система уравнений типа (
29).
Напомним, что число  , согласно нашему предположению,
существенно меньше, чем
, согласно нашему предположению,
существенно меньше, чем
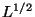 .
Поэтому оно раскладывается в
произведение простых чисел, входящих в множество
.
Поэтому оно раскладывается в
произведение простых чисел, входящих в множество
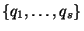 , и это
приводит к сравнению (30).
, и это
приводит к сравнению (30).
Заметим, что количество (33) найденных сравнений типа (29)
превосходит число  . Следовательно, построенная система
неоднородных линейных сравнений относительно
. Следовательно, построенная система
неоднородных линейных сравнений относительно 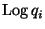 содержит сравнений больше, чем неизвестных. Конечно, множество
ее решений может при этом быть бесконечным. Одна из
правдоподобных гипотез состоит в том, что система все-таки
имеет единственное решение, и, решив ее, можно определить
дискретные логарифмы всех чисел
содержит сравнений больше, чем неизвестных. Конечно, множество
ее решений может при этом быть бесконечным. Одна из
правдоподобных гипотез состоит в том, что система все-таки
имеет единственное решение, и, решив ее, можно определить
дискретные логарифмы всех чисел  . На этом завершается
первый этап работы алгоритма из [18].
. На этом завершается
первый этап работы алгоритма из [18].
Как было отмечено, каждое из чисел, стоящих в правой части
сравнения (32), не превосходит
 . Поэтому оно
раскладывается в произведение не более
. Поэтому оно
раскладывается в произведение не более  простых
сомножителей и, следовательно, каждое из сравнений (29)
построенной системы содержит лишь
простых
сомножителей и, следовательно, каждое из сравнений (29)
построенной системы содержит лишь  отличных от нуля
коэффициентов. Матрица системы сравнений будет разреженной, что
позволяет применять для ее решения специальные методы с меньшей
оценкой сложности, чем обычный гауссов метод исключения
переменных.
отличных от нуля
коэффициентов. Матрица системы сравнений будет разреженной, что
позволяет применять для ее решения специальные методы с меньшей
оценкой сложности, чем обычный гауссов метод исключения
переменных.
Вместо перебора всех допустимых значений  в [18]
предлагается использовать так называемое решето,
отбрасывающее все пары этих чисел, для которых правая часть (32)
заведомо не раскладывается в произведение малых простых
сомножителей. Для каждого
в [18]
предлагается использовать так называемое решето,
отбрасывающее все пары этих чисел, для которых правая часть (32)
заведомо не раскладывается в произведение малых простых
сомножителей. Для каждого
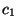 и каждой малой простой степени
и каждой малой простой степени
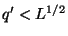 можно
найти все решения
можно
найти все решения  линейного сравнения
линейного сравнения

Организованная правильным образом, эта процедура одновременно отбирает
все нужные пары чисел

и дает разложение на простые сомножители
правых частей сравнений (32).
Итак, после первого этапа работы алгоритма в нашем распоряжении
оказываются дискретные логарифмы всех чисел из множества  .
Второй этап алгоритма сводит поиск дискретного логарифма
числа
.
Второй этап алгоритма сводит поиск дискретного логарифма
числа  к поиску логарифмов некоторого множества чисел
к поиску логарифмов некоторого множества чисел  , не
превосходящих по величине
, не
превосходящих по величине 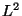 . Выбирая случайным образом
число
. Выбирая случайным образом
число  не более
не более  раз, можно, как показывают
вероятностные соображения, найти такое
раз, можно, как показывают
вероятностные соображения, найти такое  , что вычет
, что вычет
 раскладывается
в произведение простых чисел, меньших
раскладывается
в произведение простых чисел, меньших 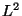 . Пусть
. Пусть

такое разложение, где

- некоторые простые
числа с условием

. На поиск этого сравнения
потребуется

арифметических операций. В результате вычисление
дискретного логарифма числа

сводится к вычислению

дискретных логарифмов для чисел

,
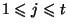
среднего
размера.
Наконец, на последнем этапе производится вычисление логарифмов всех
чисел  . Пусть
. Пусть  - простое число из интервала
- простое число из интервала
 .
Обозначим
.
Обозначим
![\begin{displaymath}G=\left[\frac{\sqrt p}{u}\right]\!,\quad I=HGu-p.\end{displaymath}](img892.gif)
Для любых целых чисел
 выполняется
сравнение
выполняется
сравнение
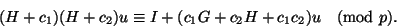 |
(34) |
Отметим, что правая часть этого сравнения не
превосходит

. Просеивая все числа

из
указанного интервала, можно найти такие, что числа
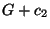
и
правая часть сравнения (
34) состоят из простых сомножителей, не
превосходящих
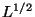
. Тогда сравнение (
34) позволяет
вычислить
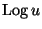
. Вычисление
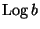
при известных уже
значениях
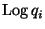
требует

арифметических операций.
Существуют и другие способы построения соотношений (28).
В [23] для этого используются вычисления в полях
алгебраических чисел. В качестве множителей в соотношениях
типа (28) используются не только простые числа, но и простые идеалы с
небольшой нормой.
Задача вычисления дискретных логарифмов может рассматриваться
также и в полях  , состоящих из
, состоящих из
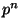 элементов, в
мультипликативных группах классов вычетов
элементов, в
мультипликативных группах классов вычетов
 , в группах точек
эллиптических кривых и вообще в произвольных группах. С
литературой по этому вопросу можно ознакомиться по работе [19].
, в группах точек
эллиптических кривых и вообще в произвольных группах. С
литературой по этому вопросу можно ознакомиться по работе [19].
Next: 4.9. Заключение
Up: 4. Алгоритмические проблемы теории
Previous: 4.7. Как раскладывают составные
Contents: Содержание