Next: Литература к главе 4 Up: 4. Алгоритмические проблемы теории Previous: 4.8. Дискретное логарифмирование Contents: Содержание

4.9. Заключение

Мы затронули в этой главе лишь небольшую часть вопросов, связанных с теоретико-числовыми алгоритмами и оценками их сложности. Мы не описывали перспективные исследования, связанные с распространением алгоритмов решета на поля алгебраических чисел (решето числового поля), и использование их для разложения целых чисел на множители или решения задачи дискретного логарифмирования, см. [20]. Именно с помощью этих алгоритмов достигнуты теоретические оценки сложности разложения на множители

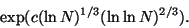
Не были затронуты эллиптические кривые, т.е. определенные с точностью до обратимого множителя пропорциональности множества точек

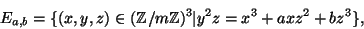
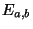
обладающие групповой структурой. С их помощью удалось построить весьма эффективные алгоритмы разложения чисел на множители и проверки целых чисел на простоту. В отличие от мультипликативной группы порядок группы при одном и том же меняется в зависимости от целых параметров , . Это оказывается весьма существенным, например, при разложении чисел на множители. Мы отсылаем читателей за подробностями использования эллиптических кривых к статье [21].

Next: Литература к главе 4 Up: 4. Алгоритмические проблемы теории Previous: 4.8. Дискретное логарифмирование Contents: Содержание