Next: 3.4. Протоколы типа ``подбрасывание
Up: 3. Криптографические протоколы
Previous: 3.2. Целостность. Протоколы аутентификации
Contents: Содержание
3.3. Неотслеживаемость. Электронные деньги
| |
``И он сделает то, что всем - малым и великим,
богатым и нищим, свободным и рабам - положено будет
начертание на правую руку их или на чело их,
И что никому нельзя будет ни покупать, ни продавать,
кроме того, кто имеет это начертание, или имя зверя, или
число имени его.
Здесь мудрость. Кто имеет ум, тот сочти число зверя,
ибо это число человеческое; число его шестьсот шестьдесят
шесть.''
|
|---|
Откровение святого Иоанна Богослова, глава 13.
Лет пятнадцать назад, а может быть и больше, жители
некоторых районов Москвы обнаруживали в своих почтовых
ящиках необычные послания. На листочках, вырванных из
ученических тетрадей, не слишком грамотные люди старательно
переписывали один и тот же текст, повествующий о том, что
где-то в Брюсселе (не иначе, как в штаб-квартире НАТО)
появился конфьютер (сохраняем терминологию авторов) под
названием ``Зверь'' и с номером 666. И этот конфьютер якобы
предначертал каждому смертному определенное число, без
которого не то что покупать или продавать, но даже шагу
ступить нельзя будет. В заключение, разумеется, предрекался
скорый конец света.
Безусловно, это сочинение, как и все ему подобные, не
заслуживало бы никакого внимания, если бы его авторы, сами
того не ведая, не нащупали весьма серьезную угрозу,
которую несет компьютеризация правам и свободам личности.
Поскольку данный раздел посвящен электронным деньгам,
рассмотрим эту угрозу на следующем простом примере. Столь
популярная ныне во всем мире кредитная карточка
представляет собой носитель информации, который при каждом
платеже полностью идентифицирует своего владельца. И если
владелец карточки использует ее для покупки билетов на
транспорт, то можно отследить все его поездки, что в
цивилизованном обществе без санкции прокурора недопустимо.
Аналогичным образом, для каждого владельца кредитных
карточек возможно собирать информацию о том, какие товары
и где он покупает, какими услугами пользуется, какие
культурно-зрелищные мероприятия посещает и т.д.
Дальше - больше. Организация компьютерного доступа к
хранилищам информации и перевод документов в электронную
форму создадут предпосылки для ведения досье, отражающих
весь круг интересов каждого из граждан. Этот перечень угроз
правам и свободам личности, безусловно, можно
продолжить1). Резюмируя, можно
сказать, что компьютеризация создает беспрецедентные
возможности для организации тотальной слежки. Угроза эта
тем более серьезная, что она до сих пор еще не осознана
даже многими специалистами.
Для предотвращения подобной угрозы необходима система
контроля за доступом к ресурсам, которая удовлетворяет
двум, казалось бы, взаимно исключающим требованиям.
Во-первых, всякий желающий должен иметь возможность
обратиться к этой системе анонимно, а во-вторых, при этом
все же доказать свое право на доступ к тому или иному
ресурсу. Обычные бумажные деньги обеспечивают оба этих
свойства. Если ресурсом, например, является некоторый
товар, то наличие у покупателя достаточного количества
купюр является доказательством его права на доступ к
ресурсу. С другой стороны, хотя каждая бумажная купюра и
имеет уникальный номер, отслеживать купюры по номерам
практически невозможно. Кредитные карточки удовлетворяют
только второму требованию.
Всюду ниже под электронными
деньгами мы будем понимать
электронные платежные средства, обеспечивающие
неотслеживаемость.
Понятие неотслеживаемости, также как и
целостности, по-видимому, не может быть формализовано и
будет поясняться на конкретных примерах протоколов.
Для работы с электронными деньгами разрабатываются
специальные криптографические протоколы, называемые
протоколами электронных платежей.
В таком протоколе
задействованы три участника, которых
мы будем называть: банк, покупатель и продавец.
Покупатель и продавец, каждый, имеют счет в банке, и
покупатель желает заплатить продавцу за товар или услугу.
В платежной системе используются три основные транзакции:
- снятие со счета;
- платеж;
- депозит.
В транзакции снятия со счета покупатель получает
подписанную банком электронную банкноту на затребованную
сумму. При этом счет покупателя уменьшается на эту
сумму. В транзакции платежа покупатель передает банкноту
продавцу и указывает сумму платежа. Продавец, в свою
очередь, передает эту информацию банку, который проверяет
подлинность банкноты. Если банкнота подлинная, банк
проверяет, не была ли она потрачена ранее. Если нет, то
банк заносит банкноту в специальный регистр, зачисляет
требуемую сумму на счет продавца, уведомляет продавца об
этом, и, если достоинство банкноты выше, чем сумма платежа,
возвращает покупателю ``сдачу'' (через продавца). С помощью
транзакции депозита, покупатель может положить ``сдачу'' на
свой счет в банке.
Безопасность банка основывается на невозможности подделать
его подпись для создания фальшивой банкноты, или, более
общим образом, на невозможности, получив набор подлинных
электронных банкнот, подделать подпись еще хотя бы для
одной банкноты. Для неотслеживаемости покупателя
необходимо, чтобы банк, получив банкноту в транзакции
платежа, не мог установить, кому она была выдана. То же
относится и к ``сдаче''. Это, казалось бы, парадоксальное
требование удовлетворяется с помощью схемы так называемой
затемненной (слепой) подписи: в транзакции снятия
со счета банк подписывает не банкноту, а некоторую
``абракадабру'', из которой покупатель восстанавливает
подписанную банкноту. Таким образом, неотслеживаемость
гарантируется тем, что банк просто не знает, что именно он
подписал.
Рассмотрим простейший вариант платежной системы, в которой
используется затемненная подпись, соответствующая схеме
подписи RSA.
Последняя основана
на тех же принципах, что и
криптосистема RSA (см. главу 4). Подписывающий, в нашем
случае - банк, выбирает два секретных простых числа  и
и
 достаточно большой длины и публикует их произведение
достаточно большой длины и публикует их произведение
 . Пусть
. Пусть 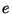 и
и  , где
, где
 , -
соответственно открытый и секретный ключи криптосистемы
RSA. Генерация подписи в схеме электронной подписи RSA
состоит в применении к сообщению
, -
соответственно открытый и секретный ключи криптосистемы
RSA. Генерация подписи в схеме электронной подписи RSA
состоит в применении к сообщению  функции дешифрования
криптосистемы RSA:
функции дешифрования
криптосистемы RSA: 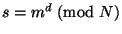 . Для проверки подписи
нужно применить к ней функцию шифрования. Если
. Для проверки подписи
нужно применить к ней функцию шифрования. Если  , то
, то  - корректная подпись для сообщения
- корректная подпись для сообщения  .
.
Итак, банк выбирает и публикует числа  и
и 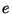 , а также
некоторую одностороннюю функцию
, а также
некоторую одностороннюю функцию
 ,
назначение которой станет ясно из дальнейшего. Пара ключей
,
назначение которой станет ясно из дальнейшего. Пара ключей
 используется банком исключительно для создания
электронных банкнот, т.е. устанавливается соглашение о
том, что электронной подписи, сгенерированной на ключе
используется банком исключительно для создания
электронных банкнот, т.е. устанавливается соглашение о
том, что электронной подписи, сгенерированной на ключе  ,
соответствует электронная банкнота достоинством,
скажем, в 1 фантик.
,
соответствует электронная банкнота достоинством,
скажем, в 1 фантик.
В транзакции снятия со счета покупатель выбирает случайное
число 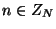 и вычисляет
и вычисляет 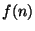 . Ему нужно
получить подпись банка на этой банкноте, т.е. значение
. Ему нужно
получить подпись банка на этой банкноте, т.е. значение
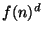 . Но просто послать значение
. Но просто послать значение 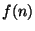 банку
покупатель не может, поскольку для снятия денег со счета он
должен идентифицировать себя. Поэтому, если банк получает
банку
покупатель не может, поскольку для снятия денег со счета он
должен идентифицировать себя. Поэтому, если банк получает
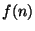 , он в дальнейшем всегда узнает данную банкноту и
неотслеживаемость будет потеряна. Решение проблемы состоит
в использовании затемненной подписи: покупатель выбирает
случайное число
, он в дальнейшем всегда узнает данную банкноту и
неотслеживаемость будет потеряна. Решение проблемы состоит
в использовании затемненной подписи: покупатель выбирает
случайное число  ,
,  , вычисляет
, вычисляет
 и посылает это значение банку.
Множитель
и посылает это значение банку.
Множитель  часто называют затемняющим множителем.
Банк вычисляет значение
часто называют затемняющим множителем.
Банк вычисляет значение
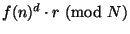 и
возвращает его покупателю. Покупатель легко ``снимает''
затемняющий множитель и получает подписанную банкноту
и
возвращает его покупателю. Покупатель легко ``снимает''
затемняющий множитель и получает подписанную банкноту
 .
.
В транзакции платежа покупатель передает продавцу
электронную банкноту
 . В принципе,
продавец может проверить подлинность любой банкноты
. В принципе,
продавец может проверить подлинность любой банкноты  самостоятельно. Для этого достаточно вычислить
самостоятельно. Для этого достаточно вычислить 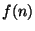 и
проверить, что
и
проверить, что
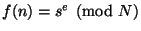 . Но дело в том, что
электронные банкноты, как и любую другую информацию,
представленную в электронной форме, легко копировать.
Поэтому нечестный покупатель может заплатить одной и той же
электронной банкнотой многократно. Для предотвращения
подобного злоупотребления продавец передает банкноту на
проверку банку. Банк проверяет по специальному регистру, не
была ли эта банкнота потрачена ранее, и если нет, то
зачисляет 1 фантик на счет продавца и уведомляет его об
этом.
. Но дело в том, что
электронные банкноты, как и любую другую информацию,
представленную в электронной форме, легко копировать.
Поэтому нечестный покупатель может заплатить одной и той же
электронной банкнотой многократно. Для предотвращения
подобного злоупотребления продавец передает банкноту на
проверку банку. Банк проверяет по специальному регистру, не
была ли эта банкнота потрачена ранее, и если нет, то
зачисляет 1 фантик на счет продавца и уведомляет его об
этом.
Безопасность банка в этой системе электронных платежей
основывается на вере в стойкость схемы
электронной подписи RSA.
Применение функции  в этой
конструкции необходимо ввиду известного свойства
мультипликативности схемы RSA: если
в этой
конструкции необходимо ввиду известного свойства
мультипликативности схемы RSA: если 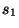 и
и 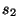 -
подписи для
-
подписи для  и
и  соответственно, то
соответственно, то
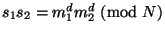 - подпись для
- подпись для  .
Поэтому, если бы в системе электронных платежей
использовались банкноты вида
.
Поэтому, если бы в системе электронных платежей
использовались банкноты вида
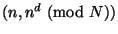 , то из двух
подлинных банкнот всегда можно было бы изготовить третью.
Неотслеживаемость клиентов в данной системе абсолютна. Все,
что остается у банка от транзакции снятия со счета, - это
значение
, то из двух
подлинных банкнот всегда можно было бы изготовить третью.
Неотслеживаемость клиентов в данной системе абсолютна. Все,
что остается у банка от транзакции снятия со счета, - это
значение
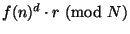 , которое благодаря
затемняющему множителю
, которое благодаря
затемняющему множителю  представляет собой просто
случайное число из
представляет собой просто
случайное число из  . Поэтому у банка нет
никакой информации о том, какую именно банкноту он выдал
данному клиенту.
. Поэтому у банка нет
никакой информации о том, какую именно банкноту он выдал
данному клиенту.
В этом примере банк выдает банкноты только достоинством
в 1 фантик и все платежи должны быть кратны этой величине.
Оказывается, можно реализовать и более гибкую систему.
Рассмотрим
следующую систему электронных платежей из работы
Шаума [9]. Здесь уместно отметить, что все основные идеи,
связанные с понятием
неотслеживаемости, электронными
деньгами и со схемами затемненной подписи, принадлежат
этому голландскому математику.
Система из работы [9] также основана на схеме электронной
подписи RSA. Допуская некоторую вольность в обозначениях
будем писать
 вместо
вместо  , где
, где
 , и называть эту величину корнем
, и называть эту величину корнем  -ой
степени из
-ой
степени из  . Как и выше,
. Как и выше,
 -
некоторая односторонняя функция, которую выбирает и
публикует банк.
-
некоторая односторонняя функция, которую выбирает и
публикует банк.
Устанавливается соглашение, согласно которому корню
степени, равной  -му нечетному простому числу,
соответствует номинал в
-му нечетному простому числу,
соответствует номинал в 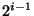 фантиков. Т.е.
предъявитель пары
фантиков. Т.е.
предъявитель пары
 является
владельцем электронной банкноты достоинством в 1 фантик.
Если в этой паре вместо корня кубического присутствует
корень 7-ой степени, то банкнота имеет достоинство 4
фантика, а если 21-ой степени - то 5 фантиков. Иными
словами, для банкноты достоинством
является
владельцем электронной банкноты достоинством в 1 фантик.
Если в этой паре вместо корня кубического присутствует
корень 7-ой степени, то банкнота имеет достоинство 4
фантика, а если 21-ой степени - то 5 фантиков. Иными
словами, для банкноты достоинством  фантиков необходим
корень степени, равной произведению всех простых чисел,
соответствующих единицам в двоичном представлении числа
фантиков необходим
корень степени, равной произведению всех простых чисел,
соответствующих единицам в двоичном представлении числа  .
.
Все банкноты, выдаваемые банком, имеют
одинаковое достоинство. Для простоты изложения будем, как и
в [9], предполагать, что оно равно 15 фантикам.
Тогда подпись банка на банкноте, это - корень  -ой
степени, где
-ой
степени, где
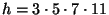 . Для этой схемы
нужен также еще дополнительный модуль RSA
. Для этой схемы
нужен также еще дополнительный модуль RSA  , который
используется в работе с так называемой копилкой (см. ниже).
Этот модуль выбирается и публикуется таким же образом, как
и модуль
, который
используется в работе с так называемой копилкой (см. ниже).
Этот модуль выбирается и публикуется таким же образом, как
и модуль  .
.
Транзакция снятия со счета выполняется таким же образом,
как описано выше. В результате покупатель получает
электронную банкноту
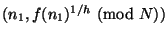 .
.
Предположим теперь, что покупатель желает заплатить
продавцу 5 фантиков. Для этого он вычисляет
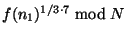 , просто возводя полученную
банкноту в 55-ую степень, и создает копилку, выбирая
случайное значение
, просто возводя полученную
банкноту в 55-ую степень, и создает копилку, выбирая
случайное значение  и вычисляя
и вычисляя
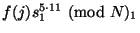 . Здесь опять
. Здесь опять
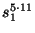 - затемняющий
множитель. Транзакция платежа начинается с пересылки
значений
- затемняющий
множитель. Транзакция платежа начинается с пересылки
значений
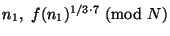 ,
,
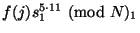 , а также суммы платежа (5
фантиков) продавцу. Продавец, в свою очередь, передает всю
эту информацию банку. Банк легко проверяет, что пара
, а также суммы платежа (5
фантиков) продавцу. Продавец, в свою очередь, передает всю
эту информацию банку. Банк легко проверяет, что пара
 представляет собой подлинную
банкноту достоинством 5 фантиков. Он проверяет по
специальному регистру, не была ли банкнота с номером
представляет собой подлинную
банкноту достоинством 5 фантиков. Он проверяет по
специальному регистру, не была ли банкнота с номером  потрачена ранее. Если нет, записывает в регистр вновь
полученную банкноту, увеличивает счет продавца на 5
фантиков и посылает продавцу уведомление о завершении
транзакции платежа, а также ``сдачу'' (10 фантиков)
покупателю, возвращаемую через копилку:
потрачена ранее. Если нет, записывает в регистр вновь
полученную банкноту, увеличивает счет продавца на 5
фантиков и посылает продавцу уведомление о завершении
транзакции платежа, а также ``сдачу'' (10 фантиков)
покупателю, возвращаемую через копилку:
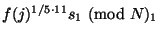 .
.
В транзакции депозита покупатель посылает
банку копилку
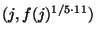 . Банк проверяет ее таким же
образом, как и банкноту в транзакции платежа, и если копилка с
номером
. Банк проверяет ее таким же
образом, как и банкноту в транзакции платежа, и если копилка с
номером  подлинная и ранее не использовалась в
транзакции депозита, то зачисляет сумму 10 фантиков на счет
покупателя.
подлинная и ранее не использовалась в
транзакции депозита, то зачисляет сумму 10 фантиков на счет
покупателя.
Если все
платежи, осуществляемые покупателями, делаются на
максимальную сумму (15 фантиков), то схема обеспечивает
безусловную (или теоретико-информационную)
неотслеживаемость покупателя: выдавая затемненную подпись,
банк не получает никакой информации о номере подписываемой
банкноты.
Необходимость депозита полученной от банка ``сдачи''
нарушает неотслеживаемость: банк запоминает все платежи, а
значит, и все ``сдачи'', и при выполнении транзакции
депозита может ``вычислить'' клиента, если последний
выполнил платеж на уникальную или достаточно редко
встречающуюся сумму. Эта проблема частично может быть
решена за счет многократного использования копилки в
транзакциях платежа.
Предположим, что покупатель получил в банке вторую банкноту
с номером  и желает заплатить тому же или другому
продавцу сумму в 3 фантика. Тогда в транзакции платежа он
может использовать копилку со ``сдачей'', оставшейся после
первого платежа, и послать продавцу
и желает заплатить тому же или другому
продавцу сумму в 3 фантика. Тогда в транзакции платежа он
может использовать копилку со ``сдачей'', оставшейся после
первого платежа, и послать продавцу  ,
,
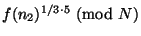 ,
,
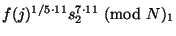 . Платеж выполняется таким же
образом, как было описано выше, и в результате покупатель
получит копилку
. Платеж выполняется таким же
образом, как было описано выше, и в результате покупатель
получит копилку
 .
.
В транзакции депозита покупатель кладет накопленную в
копилке сумму на свой счет в банке. Для этого он посылает
банку значения  ,
,
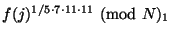 и указывает сумму. Банк проверяет копилку так
же, как банкноту, т.е. устанавливает наличие всех корней с
объявленными покупателем кратностями, а также проверяет,
что копилка с номером
и указывает сумму. Банк проверяет копилку так
же, как банкноту, т.е. устанавливает наличие всех корней с
объявленными покупателем кратностями, а также проверяет,
что копилка с номером  не использовалась ранее ни в
одной транзакции депозита. При выполнении всех этих условий
банк зачисляет сумму, находящуюся в копилке, на счет
покупателя.
не использовалась ранее ни в
одной транзакции депозита. При выполнении всех этих условий
банк зачисляет сумму, находящуюся в копилке, на счет
покупателя.
Если количество клиентов в платежной системе достаточно
велико и если каждый из них использует в транзакциях
платежа одну и ту же копилку до тех пор, пока накапливаемая
в ней сумма не превысит определенный предел (скажем, 100
фантиков), а после этого сразу же выполняет депозит, то
шансы банка отследить действия кого-либо из клиентов
представляются практически ничтожными.
Оба рассмотренных примера относятся к классу так
называемых централизованных
систем, отличительная черта
которых - необходимость участия банка во всех транзакциях
платежа. С точки зрения эффективности значительно
привлекательнее выглядят автономные
системы электронных
платежей, в которых продавец самостоятельно, без обращения
к банку, проверяет подлинность полученных от покупателя
электронных денег. Последние, чтобы отличить автономные
системы от централизованных, будем называть электронной
монетой (заметим, что общепринятой терминологии здесь нет).
Как уже отмечалось выше, без обращения к банку в каждой
транзакции платежа невозможно предотвратить повторную трату
одной и той же электронной монеты. Вместо этого автономные
системы обеспечивают идентификацию нарушителя post
factum. Конструкции автономных систем электронных платежей
достаточно сложны (см., например, [10], [11]), поэтому
здесь мы описываем лишь их основную идею, да и то в самых общих
чертах. Наше описание предполагает использование схемы
аутентификации Шнорра, но можно использовать и любую другую
схему, обладающую всеми необходимыми свойствами.
Каждый клиент банка выбирает секретный ключ  , содержащий
идентификатор этого клиента, и затем вычисляет открытый ключ
, содержащий
идентификатор этого клиента, и затем вычисляет открытый ключ
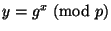 . В транзакции снятия со счета клиент
выбирает случайное значение
. В транзакции снятия со счета клиент
выбирает случайное значение  и вычисляет
и вычисляет  . Электронная
монета состоит из некоторой строки, содержащей
. Электронная
монета состоит из некоторой строки, содержащей  и
и  , и подписи
банка для этой строки. Основная трудность здесь состоит в том, что банк
должен подписать монету затемненной подписью, но при этом убедиться в
том, что монета имеет требуемую структуру. Один из способов решения
этой проблемы заинтересованный читатель может найти в работе
Якоби [10].
, и подписи
банка для этой строки. Основная трудность здесь состоит в том, что банк
должен подписать монету затемненной подписью, но при этом убедиться в
том, что монета имеет требуемую структуру. Один из способов решения
этой проблемы заинтересованный читатель может найти в работе
Якоби [10].
В транзакции платежа продавец сначала проверяет подпись
банка, и, если она корректна, выбирает случайный запрос 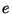 ,
как в схеме аутентификации Шнорра, и посылает
,
как в схеме аутентификации Шнорра, и посылает 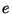 покупателю. Последний вычисляет
покупателю. Последний вычисляет
 и посылает
и посылает
 продавцу. Продавец проверяет правильность ответа,
используя те значения
продавцу. Продавец проверяет правильность ответа,
используя те значения  и
и  , которые содержатся в
монете.
, которые содержатся в
монете.
В транзакции депозита продавец посылает банку электронную
монету, а также 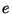 и
и  . Если банк обнаруживает, что
данная монета уже была потрачена ранее, то у него
оказываются две различные пары
. Если банк обнаруживает, что
данная монета уже была потрачена ранее, то у него
оказываются две различные пары 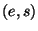 и
и 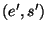 ,
удовлетворяющие проверочному соотношению в схеме Шнорра при
одних и тех же
,
удовлетворяющие проверочному соотношению в схеме Шнорра при
одних и тех же  и
и  . Как было показано в предыдущем
разделе, этого достаточно для того, чтобы банк смог
вычислить секретный ключ
. Как было показано в предыдущем
разделе, этого достаточно для того, чтобы банк смог
вычислить секретный ключ  , а значит, и идентифицировать
нарушителя.
, а значит, и идентифицировать
нарушителя.
Замечательное свойство автономных систем электронных
платежей состоит в том, что они, с одной стороны,
обеспечивают неотслеживаемость честных клиентов, а с
другой - позволяют однозначно идентифицировать нарушителей. Но в
таких системах банк идет на определенный риск, поскольку в
момент обнаружения повторной траты электронной монеты на
счету нарушителя может не оказаться суммы, достаточной для
покрытия перерасхода. Несколько более подробно эта проблема
обсуждается в [12].
В большинстве автономных систем
электронные монеты могут
использоваться лишь в одном платеже, после чего необходимо
выполнить депозит. Если
монета может использоваться во
многих платежах, без промежуточных депозитов, то такая
монета называется переводимой. Если бы переводимые монеты
могли находиться в обращении достаточно долго, то это
обеспечило бы практическую неотслеживаемость клиентов. Но с
другой стороны, стало бы значительно сложнее обнаруживать
повторные траты одной и той же монеты. Еще один недостаток
в том, что длина переводимой монеты возрастает с каждым ее
переводом от клиента к клиенту. С интуитивной точки зрения
это представляется естественным, поскольку монета должна
содержать информацию, позволяющую банку идентифицировать
нарушителя, потратившего монету дважды. Поэтому каждый
клиент, через которого проходит монета, должен оставить на
ней свои ``отпечатки пальцев''. Шаум и Педерсен [13]
доказали, что возрастание длины переводимой монеты и в
самом деле неизбежно.
Next: 3.4. Протоколы типа ``подбрасывание
Up: 3. Криптографические протоколы
Previous: 3.2. Целостность. Протоколы аутентификации
Contents: Содержание