Next: 3.3. Неотслеживаемость. Электронные деньги
Up: 3. Криптографические протоколы
Previous: 3.1. Введение
Contents: Содержание
| |
``Воротится коза, постучится в дверь и запоет:
- Козлятушки, ребятушки!
Отопритеся, отворитеся!
Ваша мать пришла - молока принесла.
Козлятки отопрут дверь и впустят мать...
Волк подслушал как поет коза. Вот раз коза ушла, волк
подбежал к избушке и закричал толстым голосом:
- Вы детушки! Вы козлятушки!
Отопритеся, отворитеся,
Ваша мать пришла, молока принесла.
Козлята ему отвечают:
- Слышим, слышим - да не матушкин это голосок!...
Волку делать нечего. Пошел он в кузницу и велел себе
горло перековать, чтобы петь тонюсеньким голосом...
Только коза ушла, волк опять шасть к избушке,
постучался и начал причитывать тонюсеньким голосом:
- Козлятушки, ребятушки!
Отопритеся, отворитеся!
Ваша мать пришла - молока принесла.
Козлята отворили дверь, волк кинулся в избу и всех
козлят съел.''
|
|---|
``Волк и семеро козлят''.
Русская народная сказка.
Как уже отмечалось во введении, понятие целостности
информации, по-видимому, не допускает математической
формализации. В данном разделе мы
рассмотрим методы
обеспечения целостности на примере двух наиболее важных и
распространенных типов криптографических протоколов -
схем аутентификации и электронной подписи.
Назначение и суть протоколов
аутентификации (называемых
также протоколами идентификации) легко понять на следующем
примере. Представим себе информационную систему, которая
работает в компьютерной сети и обеспечивает доступ к
некоторым данным. У администратора системы имеется список
всех ее пользователей вместе с сопоставленным каждому из
них набором полномочий, на основе которых осуществляется
разграничение доступа к ресурсам системы. Ресурсами могут
быть, например, некоторые фрагменты информации, а также
функции, выполняемые системой. Одним пользователям может
быть разрешено читать одну часть информации, другим -
другую ее часть, а третьим - еще и вносить в нее
изменения. В данном контексте под обеспечением целостности
понимается предотвращение доступа к системе лиц, не
являющихся ее пользователями, а также предотвращение доступа
пользователей к тем ресурсам, на которые у них нет полномочий.
Наиболее распространенный метод разграничения доступа, парольная
защита, имеет массу недостатков. Их обсуждение стало общим
местом для текстов по компьютерной безопасности, поэтому мы
сразу перейдем к криптографической постановке задачи.
В протоколе имеются два участника - Алиса, которая должна
доказать свою аутентичность, и Боб, который эту
аутентичность должен проверить. У Алисы имеются два ключа
- общедоступный открытый  и секретный
и секретный  .
Фактически, Алисе нужно доказать, что она знает
.
Фактически, Алисе нужно доказать, что она знает  , и
сделать это таким образом, чтобы это доказательство можно
было проверить, зная только
, и
сделать это таким образом, чтобы это доказательство можно
было проверить, зная только  .
.
Задача аутентификации уже обсуждалась в главе 2. Там же были
сформулированы основные требования, которым должен
удовлетворять стойкий протокол аутентификации. Напомним,
что для удовлетворения этих требований достаточно, чтобы
протокол аутентификации был доказательством с нулевым
разглашением. В главе 2 приведен протокол доказательства с
абсолютно нулевым разглашением для задачи ИЗОМОРФИЗМ
ГРАФОВ. Но этот протокол имеет неприемлемо большое с
практической точки зрения количество раундов обмена
сообщениями между Алисой и Бобом.
Ниже мы приводим протокол
Шнорра [1], один из наиболее
эффективных практических протоколов аутентификации. Для его
описания нам потребуются некоторые обозначения, которые
будут использоваться и в последующих разделах данной главы.
Пусть  и
и  - простые числа такие, что
- простые числа такие, что  делит
делит
 . Шнорр предлагает [1] использовать
. Шнорр предлагает [1] использовать  длины порядка
512 битов и
длины порядка
512 битов и  - длины порядка 140 битов. Пусть
- длины порядка 140 битов. Пусть 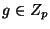 таково, что
таково, что 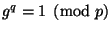 ,
, 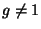 . Пусть
. Пусть  и
и 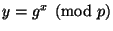 . Задача
вычисления значения
. Задача
вычисления значения  по
заданному значению
по
заданному значению  при известных
при известных  ,
,  и
и  называется задачей дискретного
логарифмирования (см. главу 4).
Для задачи дискретного логарифмирования на данный
момент не известно эффективных алгоритмов. Поэтому в
криптографии широко используется
гипотеза
о вычислительной трудности задачи дискретного логарифмирования. Сформулируем
ее более строго. Пусть
называется задачей дискретного
логарифмирования (см. главу 4).
Для задачи дискретного логарифмирования на данный
момент не известно эффективных алгоритмов. Поэтому в
криптографии широко используется
гипотеза
о вычислительной трудности задачи дискретного логарифмирования. Сформулируем
ее более строго. Пусть  - растущий
целочисленный параметр, число
- растущий
целочисленный параметр, число  выбирается из множества
всех простых чисел длины
выбирается из множества
всех простых чисел длины  таких, что
таких, что  имеет простой делитель
длины не меньше
имеет простой делитель
длины не меньше 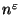 для некоторой константы
для некоторой константы
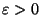 ,
,  - из множества всех таких простых
делителей числа
- из множества всех таких простых
делителей числа  ,
,  -
из множества всех чисел
-
из множества всех чисел  таких, что
таких, что 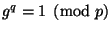 , а
, а
 . Тогда функция
. Тогда функция
 -
односторонняя (см. главу 2). Рекомендации, данные
Шнорром относительно длин чисел
-
односторонняя (см. главу 2). Рекомендации, данные
Шнорром относительно длин чисел  и
и  , можно трактовать
следующим образом. На тот момент (1989 г.)
инвертирование функции
, можно трактовать
следующим образом. На тот момент (1989 г.)
инвертирование функции  считалось практически
невыполнимым уже для
считалось практически
невыполнимым уже для  и
и  длины порядка 512 и 140
битов соответственно. Здесь, однако, следует учитывать, что
прогресс в области вычислительной техники и в
алгоритмической теории чисел (см. главу 4) может привести к
необходимости пересмотра этих величин.
длины порядка 512 и 140
битов соответственно. Здесь, однако, следует учитывать, что
прогресс в области вычислительной техники и в
алгоритмической теории чисел (см. главу 4) может привести к
необходимости пересмотра этих величин.
В качестве секретного ключа схемы аутентификации Алиса
выбирает случайное число  из
из
 . Далее
Алиса вычисляет
. Далее
Алиса вычисляет
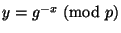 и публикует открытый ключ
и публикует открытый ключ
 . Открытые
ключи всех участников схемы должны
публиковаться таким образом, чтобы исключалась возможность
их подмены (такое хранилище ключей называется
общедоступным сертифицированным справочником). Эта
проблема, называемая часто проблемой аутентичности открытых
ключей, составляет отдельный предмет исследований в
криптографии и в данной главе не рассматривается.
. Открытые
ключи всех участников схемы должны
публиковаться таким образом, чтобы исключалась возможность
их подмены (такое хранилище ключей называется
общедоступным сертифицированным справочником). Эта
проблема, называемая часто проблемой аутентичности открытых
ключей, составляет отдельный предмет исследований в
криптографии и в данной главе не рассматривается.
Next: 3.3. Неотслеживаемость. Электронные деньги
Up: 3. Криптографические протоколы
Previous: 3.1. Введение
Contents: Содержание