Next: 3.5. Еще раз о Up: 3. Криптографические протоколы Previous: 3.3. Неотслеживаемость. Электронные деньги Contents: Содержание

3.4. Протоколы типа ``подбрасывание монеты по телефону''

``- Хорошо, дайте же сюда деньги. - На что-ж деньги? У меня вот они в руке! Как только напишете расписку, в ту же минуту их возьмете. - Да позвольте, как же мне писать расписку? Прежде нужно видеть деньги. Чичиков выпустил из рук бумажки Собакевичу, который, приблизившись к столу и накрывши их пальцами левой руки, другою написал на лоскутке бумаги, что задаток двадцать пять рублей государственными ассигнациями за проданные души получен сполна.''

Н. В. Гоголь. ``Мертвые души'', глава 5.

В данном разделе мы кратко обсудим те типы криптографических протоколов, в которых два участника должны обменяться некоторой информацией. Но участники не доверяют друг другу и каждый из них может оказаться обманщиком. Поэтому, если один из участников по неосторожности ``выпустит информацию из рук'' преждевременно, то в обмен он может получить совсем не то, проблемы здесь те же, что и в ``протоколе'' обмена расписки на ассигнации у Чичикова и Собакевича.

Из всех криптографических протоколов данного типа, пожалуй, наиболее наглядным, и к тому же достаточно простым, является протокол подбрасывания монеты. Предположим, что двум участникам, Алисе и Бобу, необходимо бросить жребий. В случае, когда они оба физически находятся в одном и том же месте, задачу можно решить с помощью обычной процедуры подбрасывания монеты. Если кто-либо из участников не доверяет монете, можно использовать другие источники случайности. Правда, создание надежных источников случайности - весьма непростая задача, но она уже относится к математической статистике, а не к криптографии.

Если же Алиса и Боб удалены друг от друга и могут общаться лишь по каналу связи, то задача о жребии, на первый взгляд, кажется неразрешимой. В самом деле, если, следуя обычной процедуре подбрасывания монеты, первый ход делает Алиса, которая выбирает один из возможных вариантов - ``орел'' или ``решка'', то Боб всегда может объявить тот исход, который ему выгоден.

Тем не менее, эта задача была решена Блюмом [14]. Любопытно, что даже в заголовке своей работы Блюм охарактеризовал предложенный им метод как метод ``решения нерешаемых задач''.

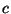Легко понять, что задача о жребии решается очень просто, если существует надежный агент - третья сторона, которая пользуется полным доверием и Алисы, и Боба, и которая имеет конфиденциальные (закрытые) каналы связи с обоими участниками. В этом случае Боб и Алиса выбирают случайные биты и соответственно и посылают их в тайне друг от друга агенту. Последний ждет, пока не поступят оба бита, и после этого публикует , 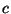и - исход подбрасывания монеты.

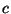В отсутствие надежного агента срабатывает идея, которую проще всего понять на следующей ``физической'' реализации. Боб выбирает случайный бит , записывает его на листе бумаги, запирает этот лист в ящике, оставляя ключ от замка у себя, и посылает ящик Алисе. Предполагается, что, не имея ключа, Алиса не может добраться до содержимого ящика. Получив ящик, Алиса выбирает случайный бит и посылает его Бобу. В ответ Боб посылает Алисе ключ от ящика. Исходом подбрасывания монеты будет опять-таки бит .

Ниже мы излагаем криптографическую реализацию той же идеи, основанную на задаче дискретного логарифмирования, и используем при этом обозначения из раздела 3.

Next: 3.5. Еще раз о Up: 3. Криптографические протоколы Previous: 3.3. Неотслеживаемость. Электронные деньги Contents: Содержание