1.4. Новые направления

Next: 1.5. Заключение Up: 1. Основные понятия криптографии Previous: 1.3. Математические основы Contents: Содержание

1.4. Новые направления

В 1983 году в книге ``Коды и математика'' М.Н.Аршинова и Л.Е.Садовского (библиотечка ``Квант'') было написано: ``Приемов тайнописи - великое множество, и, скорее всего, это та область, где уже нет нужды придумывать что-нибудь существенно новое.'' Однако это было очередное большое заблуждение относительно криптографии. Еще в 1976 году была опубликована работа молодых американских математиков У.Диффи и М.Э.Хеллмана ``Новые направления в криптографии''1), которая не только существенно изменила криптографию, но и привела к появлению и бурному развитию новых направлений в математике. Центральным понятием ``новой криптографии'' является понятие односторонней функции (подробнее об этом см. главу 2).

Односторонней называется функция $F\colon X\rightarrow Y$ , обладающая двумя свойствами:
а) существует полиномиальный алгоритм вычисления значений ;
б) не существует полиномиального алгоритма инвертирования функции (т.е. решения уравнения относительно , точное определение см. на стр. ).

Отметим, что односторонняя функция существенно отличается от функций, привычных со школьной скамьи, из-за ограничений на сложность ее вычисления и инвертирования. Вопрос о существовании односторонних функций пока открыт.

Еще одним новым понятием является понятие функции с секретом. Иногда еще употребляется термин функция с ловушкой. Функцией с секретом называется функция $F_K\colon X\rightarrow Y$ , зависящая от параметра и обладающая тремя свойствами:

а) существует полиномиальный алгоритм вычисления значения для любых и ;

б) не существует полиномиального алгоритма инвертирования при неизвестном ;

в) существует полиномиальный алгоритм инвертирования при известном .

Про существование функций с секретом можно сказать то же самое, что сказано про односторонние функции. Для практических целей криптографии было построено несколько функций, которые могут оказаться функциями с секретом. Для них свойство б) пока строго не доказано, но считается, что задача инвертирования эквивалентна некоторой давно изучаемой трудной математической задаче. Наиболее известной и популярной из них является теоретико-числовая функция, на которой построен шифр RSA (подробнее об этом см. главу 4).

Применение функций с секретом в криптографии позволяет:

1) организовать обмен шифрованными сообщениями с использованием только открытых каналов связи, т.е. отказаться от секретных каналов связи для предварительного обмена ключами;

2) включить в задачу вскрытия шифра трудную математическую задачу и тем самым повысить обоснованность стойкости шифра;

3) решать новые криптографические задачи, отличные от шифрования (электронная цифровая подпись и др.).

Опишем, например, как можно реализовать п. 1). Пользователь , который хочет получать шифрованные сообщения, должен выбрать какую-нибудь функцию с секретом . Он сообщает всем заинтересованным (например, публикует) описание функции в качестве своего алгоритма шифрования. Но при этом значение секрета он никому не сообщает и держит в секрете. Если теперь пользователь хочет послать пользователю защищаемую информацию $x\in X$ , то он вычисляет и посылает по открытому каналу пользователю . Поскольку для своего секрета умеет инвертировать , то он вычисляет по полученному . Никто другой не знает и поэтому в силу свойства б) функции с секретом не сможет за полиномиальное время по известному шифрованному сообщению вычислить защищаемую информацию .

Описанную систему называют криптосистемой с открытым ключом, поскольку алгоритм шифрования является общедоступным или открытым. В последнее время такие криптосистемы еще называют асимметричными, поскольку в них есть асимметрия в алгоритмах: алгоритмы шифрования и дешифрования различны. В отличие от таких систем традиционные шифры называют симметричными: в них ключ для шифрования и дешифрования один и тот же. Для асимметричных систем алгоритм шифрования общеизвестен, но восстановить по нему алгоритм дешифрования за полиномиальное время невозможно.

Описанную выше идею Диффи и Хеллман предложили использовать также для электронной цифровой подписи сообщений, которую невозможно подделать за полиномиальное время. Пусть пользователю необходимо подписать сообщение . Он, зная секрет , находит такое , что , и вместе с сообщением посылает пользователю в качестве своей цифровой подписи. Пользователь хранит в качестве доказательства того, что подписал сообщение .

Сообщение, подписанное цифровой подписью, можно представлять себе как пару , где - сообщение, - решение уравнения $F_K(y)=\nobreak x$ , $F_K\colon X\rightarrow Y$ - функция с секретом, известная всем взаимодействующим абонентам. Из определения функции очевидны следующие полезные свойства цифровой подписи:

1) подписать сообщение , т.е. решить уравнение , может только абонент - обладатель данного секрета ; другими словами, подделать подпись невозможно;

2) проверить подлинность подписи может любой абонент, знающий открытый ключ, т.е. саму функцию ;

3) при возникновении споров отказаться от подписи невозможно в силу ее неподделываемости;

4) подписанные сообщения можно, не опасаясь ущерба, пересылать по любым каналам связи.

Кроме принципа построения криптосистемы с открытым ключом, Диффи и Хеллман в той же работе предложили еще одну новую идею - открытое распределение ключей. Они задались вопросом: можно ли организовать такую процедуру взаимодействия абонентов и по открытым каналам связи, чтобы решить следующие задачи:

1) вначале у и нет никакой общей секретной информации, но в конце процедуры такая общая секретная информация (общий ключ) у и появляется, т.е. вырабатывается;

2) пассивный противник, который перехватывает все передачи информации и знает, что хотят получить и , тем не менее не может восстановить выработанный общий ключ и .

Диффи и Хеллман предложили решать эти задачи с помощью функции

$\begin{displaymath} F(x)=\alpha^x \pmod p, \end{displaymath}$

где

- большое простое число,

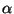
- произвольное натуральное число, $\alpha$ - некоторый примитивный элемент поля

. Общепризнанно, что инвертирование функции $\alpha^x \pmod p$ , т.е. дискретное логарифмирование, является трудной математической задачей. (Подробнее см. главу 4.)

Сама процедура или, как принято говорить, протокол выработки общего ключа описывается следующим образом.

Абоненты и независимо друг от друга случайно выбирают по одному натуральному числу - скажем и . Эти элементы они держат в секрете. Далее каждый из них вычисляет новый элемент:

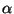
$\begin{displaymath} y_A=\alpha^{x_A} \pmod p, \quad y_B=\alpha^{x_B} \pmod p. \end{displaymath}$

(Числа

и $\alpha$ считаются общедоступными.) Потом они обмениваются этими элементами по каналу связи. Теперь абонент

, получив

и зная свой секретный элемент

, вычисляет новый элемент:

$\begin{displaymath} y^{x_A}_B \pmod p= (\alpha^{x_B})^{x_A} \pmod p. \end{displaymath}$

Аналогично поступает абонент

$\begin{displaymath} y^{x_B}_A \pmod p= (\alpha^{x_A})^{x_B} \pmod p. \end{displaymath}$

Тем самым у

появился общий элемент поля, равный $\alpha^{x_Ax_B}$ . Этот элемент и объявляется общим ключом

Из описания протокола видно, что противник знает $p,\alpha,\alpha^{x_A},\alpha^{x_B}$ , не знает и и хочет узнать $\alpha^{x_Ax_B}$ . В настоящее время нет алгоритмов действий противника, более эффективных, чем дискретное логарифмирование, а это - трудная математическая задача.

Успехи, достигнутые в разработке схем цифровой подписи и открытого распределения ключей, позволили применить эти идеи также и к другим задачам взаимодействия удаленных абонентов. Так возникло большое новое направление теоретической криптографии - криптографические протоколы (подробнее см. главу 3).

Объектом изучения теории криптографических протоколов являются удаленные абоненты, взаимодействующие, как правило, по открытым каналам связи. Целью взаимодействия абонентов является решение какой-то задачи. Имеется также противник, который преследует собственные цели. При этом противник в разных задачах может иметь разные возможности: например, может взаимодействовать с абонентами от имени других абонентов или вмешиваться в обмены информацией между абонентами и т.д. Противником может даже оказаться один из абонентов или несколько абонентов, вступивших в сговор.

Приведем еще несколько примеров задач, решаемых удаленными абонентами. (Читателю рекомендуем по своему вкусу самостоятельно придумать еще какие-нибудь примеры.)

1. Взаимодействуют два не доверяющих друг другу абонента. Они хотят подписать контракт. Это надо сделать так, чтобы не допустить следующую ситуацию: один из абонентов получил подпись другого, а сам не подписался.

Протокол решения этой задачи принято называть протоколом подписания контракта.

2. Взаимодействуют два не доверяющих друг другу абонента. Они хотят бросить жребий с помощью монеты. Это надо сделать так, чтобы абонент, подбрасывающий монету, не мог изменить результат подбрасывания после получения догадки от абонента, угадывающего этот результат.

Протокол решения этой задачи принято называть протоколом подбрасывания монеты.

Опишем один из простейших протоколов подбрасывания монеты по телефону (так называемая схема Блюма-Микали). Для его реализации у абонентов и должна быть односторонняя функция $f\colon X\to Y$ , удовлетворяющая следующим условиям:

1) - множество целых чисел, которое содержит одинаковое количество четных и нечетных чисел;

2) любые числа $x_1,x_2\in X$ , имеющие один образ , имеют одну четность;

3) по заданному образу ``трудно'' вычислить четность неизвестного аргумента .

Роль подбрасывания монеты играет случайный и равновероятный выбор элемента $x\in X$ , а роль орла и решки - четность и нечетность соответственно. Пусть - абонент, подбрасывающий монету, а - абонент, угадывающий результат. Протокол состоит из следующих шагов:

1) выбирает (``подбрасывает монету''), зашифровывает , т. e. вычисляет , и посылает абоненту ;

2) получает , пытается угадать четность и посылает свою догадку абоненту ;

3) получает догадку от и сообщает , угадал ли он, посылая ему выбранное число ;

4) проверяет, не обманывает ли , вычисляя значение и сравнивая его с полученным на втором шаге значением .

3. Взаимодействуют два абонента и (типичный пример: - клиент банка, - банк). Абонент хочет доказать абоненту , что он именно , а не противник.

Протокол решения этой задачи принято называть протоколом идентификации абонента.

4. Взаимодействуют несколько удаленных абонентов, получивших приказы из одного центра. Часть абонентов, включая центр, могут быть противниками. Необходимо выработать единую стратегию действий, выигрышную для абонентов.

Эту задачу принято называть задачей о византийских генералах, а протокол ее решения - протоколом византийского соглашения.

Осмысление различных протоколов и методов их построения привело в 1985-1986 г.г. к появлению двух плодотворных математических моделей - интерактивной системы доказательства и доказательства с нулевым разглашением. Математические исследования этих новых объектов позволили доказать много утверждений, весьма полезных при разработке криптографических протоколов (подробнее об этом см. главу 2).

Под интерактивной системой доказательства понимают протокол взаимодействия двух абонентов: (доказывающий) и (проверяющий). Абонент хочет доказать , что утверждение истинно. При этом абонент самостоятельно, без помощи , не может проверить утверждение (поэтому и называется проверяющим). Абонент может быть и противником, который хочет доказать , что утверждение истинно, хотя оно ложно. Протокол может состоять из многих раундов обмена сообщениями между и и должен удовлетворять двум условиям:

1) полнота - если действительно истинно, то абонент убедит абонента признать это;

2) корректность - если ложно, то абонент вряд ли убедит абонента , что истинно.

Здесь словами ``вряд ли'' мы для простоты заменили точную математическую формулировку.

Подчеркнем, что в определении системы не допускалось, что может быть противником. А если оказался противником, который хочет ``выведать'' у какую-нибудь новую полезную для себя информацию об утверждении ? В этом случае , естественно, может не хотеть, чтобы это случилось в результате работы протокола . Протокол , решающий такую задачу, называется доказательством с нулевым разглашением и должен удовлетворять, кроме условий 1) и 2), еще и следующему условию:

3) нулевое разглашение - в результате работы протокола абонент не увеличит свои знания об утверждении или, другими словами, не сможет извлечь никакой информации о том, почему истинно.

Next: 1.5. Заключение Up: 1. Основные понятия криптографии Previous: 1.3. Математические основы Contents: Содержание