Next: 5.3. Линейное разделение секрета
Up: 5. Математика разделения секрета
Previous: 5.1. Введение
Contents: Содержание
5.2. Разделение секрета для произвольных структур доступа
Начнем с формальной математической модели. Имеется 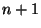 множество
множество
 и
(совместное) распределение вероятностей
и
(совместное) распределение вероятностей  на их декартовом произведении
на их декартовом произведении
 .
Соответствующие случайные величины обозначаются через
.
Соответствующие случайные величины обозначаются через
 . Имеется также некоторое множество
. Имеется также некоторое множество  подмножеств множества
подмножеств множества  , называемое
структурой доступа.
, называемое
структурой доступа.
Определение 1.
Пара 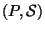 называется совершенной вероятностной
СРС, реализующей структуру доступа
называется совершенной вероятностной
СРС, реализующей структуру доступа  , если
, если
 |
(1) |
 |
(2) |
Это определение можно истолковать следующим образом. Имеется
множество 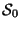 всех возможных секретов, из которого секрет
всех возможных секретов, из которого секрет  выбирается с вероятностью
выбирается с вероятностью  , и имеется СРС, которая ``распределяет''
секрет
, и имеется СРС, которая ``распределяет''
секрет  между
между  участниками, посылая ``проекции''
участниками, посылая ``проекции''
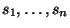 секрета с вероятностью
секрета с вероятностью
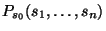 . Отметим, что
. Отметим, что
 -й участник получает свою ``проекцию''
-й участник получает свою ``проекцию''
 и не имеет
информации о значениях других ``проекций'', однако знает все множества
и не имеет
информации о значениях других ``проекций'', однако знает все множества
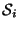 , а также оба распределения вероятностей
, а также оба распределения вероятностей  и
и
 Эти два распределения могут быть эквивалентно
заменены на одно:
Эти два распределения могут быть эквивалентно
заменены на одно:
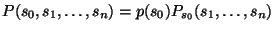 , что и было сделано выше.
Цель СРС, как указывалось во введении, состоит в том,
чтобы:
, что и было сделано выше.
Цель СРС, как указывалось во введении, состоит в том,
чтобы:
а) участники из разрешенного множества  (т.е.
(т.е. 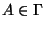 ) вместе могли бы однозначно восстановить значение
секрета - это отражено в свойстве (1);
) вместе могли бы однозначно восстановить значение
секрета - это отражено в свойстве (1);
б) участники,
образующие неразрешенное множество  (
(
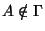 ), не могли бы
получить дополнительную информацию об
), не могли бы
получить дополнительную информацию об  ,
т.е., чтобы вероятность того, что значение секрета
,
т.е., чтобы вероятность того, что значение секрета
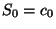 , не зависела от значений ``проекций''
, не зависела от значений ``проекций''  при
при  - это свойство (2).
- это свойство (2).
Замечание о терминологии. В англоязычной литературе для обозначения
``порции'' информации, посылаемой участнику СРС, были введены термины
``share'' (А. Шамир) и ``shadow'' (Г. Блейкли). Первый термин оказался наиболее
популярным и автор долго боролся с соблазном привлечь массового читателя,
постоянно используя в качестве его перевода слово ``акция''.
Неадекватная (во всех смыслах) замена ``акции'' на ``проекцию'' может быть
несколько оправдана следующим примером.
Пример 1.
Множество 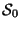 всех
возможных секретов состоит из
всех
возможных секретов состоит из  ,
,  и
и 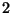 , ``представленных''
соответственно: шаром; кубом, ребра которого параллельны осям координат;
цилиндром, образующие которого параллельны оси
, ``представленных''
соответственно: шаром; кубом, ребра которого параллельны осям координат;
цилиндром, образующие которого параллельны оси  .
При этом диаметры шара и основания цилиндра, и длины ребра куба и образующей
цилиндра, равны. Первый участник получает в качестве своей ``доли'' секрета его
проекцию на плоскость
.
При этом диаметры шара и основания цилиндра, и длины ребра куба и образующей
цилиндра, равны. Первый участник получает в качестве своей ``доли'' секрета его
проекцию на плоскость  , а второй - на плоскость
, а второй - на плоскость  . Ясно, что вместе
они однозначно восстановят секрет, а порознь - не могут. Однако, эта СРС не
является совершенной, так как любой из участников получает информацию о
секрете, оставляя только два значения секрета как возможные при данной
проекции (например, если проекция - квадрат, то шар невозможен).
. Ясно, что вместе
они однозначно восстановят секрет, а порознь - не могут. Однако, эта СРС не
является совершенной, так как любой из участников получает информацию о
секрете, оставляя только два значения секрета как возможные при данной
проекции (например, если проекция - квадрат, то шар невозможен).
Еще одно замечание. Элемент
(участник)
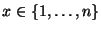 называется
несущественным (относительно
называется
несущественным (относительно  ), если для любого неразрешенного
множества
), если для любого неразрешенного
множества  множество
множество 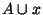 также неразрешенное. Очевидно, что
несущественные участники настолько несущественны для разделения
секрета, что им просто не нужно посылать никакой информации. Поэтому
далее, без ограничения общности, рассматриваются только такие структуры
доступа
также неразрешенное. Очевидно, что
несущественные участники настолько несущественны для разделения
секрета, что им просто не нужно посылать никакой информации. Поэтому
далее, без ограничения общности, рассматриваются только такие структуры
доступа  , для которых все элементы являются существенными.
Кроме того, естественно предполагать, что
, для которых все элементы являются существенными.
Кроме того, естественно предполагать, что
 является монотонной
структурой, т.е. из
является монотонной
структурой, т.е. из
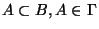 следует
следует 
Пример 2.
Рассмотрим простейшую структуру доступа - 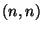 -пороговую
схему, т.е. все участники вместе могут восстановить секрет, а любое
подмножество участников не может получить дополнительной информации о
секрете. Будем строить идеальную СРС, выбирая и секрет, и его проекции из
группы
-пороговую
схему, т.е. все участники вместе могут восстановить секрет, а любое
подмножество участников не может получить дополнительной информации о
секрете. Будем строить идеальную СРС, выбирая и секрет, и его проекции из
группы 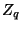 вычетов по модулю
вычетов по модулю  , т.е.
, т.е.
 Дилер
генерирует
Дилер
генерирует  независимых
равномерно распределенных на
независимых
равномерно распределенных на 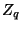 случайных
величин
случайных
величин 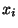 и посылает
и посылает  -му участнику
(
-му участнику
(
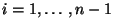 ) его ``проекцию''
) его ``проекцию'' 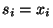 , а
, а  -му участнику
посылает
-му участнику
посылает
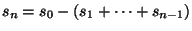 .
Кажущееся ``неравноправие''
.
Кажущееся ``неравноправие''  -ого
участника тут же исчезает, если мы выпишем распределение
-ого
участника тут же исчезает, если мы выпишем распределение
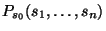 , которое очевидно
равно
, которое очевидно
равно  , если
, если
 , и равно
, и равно  - в остальных случаях.
Теперь легко проверяется и свойство (2),
означающее в данном случае независимость случайной величины
- в остальных случаях.
Теперь легко проверяется и свойство (2),
означающее в данном случае независимость случайной величины
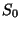 от случайных величин
от случайных величин
 при любом
собственном подмножестве
при любом
собственном подмножестве  .
.
Данное выше определение СРС, оперирующее словами ``распределение
вероятностей'', ниже переведено, почти без потери общности, на
комбинаторный язык, который представляется автору более простым для
понимания.
Произвольная 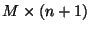 -матрица
-матрица  , строки которой имеют вид
, строки которой имеют вид
 , где
, где
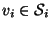 , называется матрицей
комбинаторной СРС, а ее строки - ``правилами'' распределения секрета. Для
заданного значения секрета
, называется матрицей
комбинаторной СРС, а ее строки - ``правилами'' распределения секрета. Для
заданного значения секрета  дилер СРС случайно и равновероятно
выбирает строку
дилер СРС случайно и равновероятно
выбирает строку  из тех строк матрицы
из тех строк матрицы  , для которых значение
нулевой координаты равно
, для которых значение
нулевой координаты равно  .
.
Определение 2.
Матрица  задает совершенную комбинаторную
СРС, реализующую структуру доступа
задает совершенную комбинаторную
СРС, реализующую структуру доступа  , если, во-первых, для любого
множества
, если, во-первых, для любого
множества 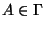 нулевая координата любой строки матрицы
нулевая координата любой строки матрицы  однозначно определяется значениями ее координат из множества
однозначно определяется значениями ее координат из множества  , и,
во-вторых, для любого множества
, и,
во-вторых, для любого множества
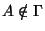 и любых заданных
значений координат из множества
и любых заданных
значений координат из множества  число строк матрицы
число строк матрицы  с данным
значением
с данным
значением 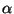 нулевой координаты не зависит от
нулевой координаты не зависит от 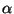 .
.
Сопоставим совершенной вероятностной СРС, задаваемой парой
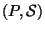 , матрицу
, матрицу 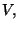 состоящую из
строк
состоящую из
строк 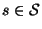 , таких что
, таких что  .
Заметим, что если в
определении 1 положить
все ненулевые значения
.
Заметим, что если в
определении 1 положить
все ненулевые значения  одинаковыми, а условия (1) и
(2)
переформулировать на комбинаторном языке, то получится
определение 2.
Это комбинаторное определение несколько обобщается, если допустить в
матрице
одинаковыми, а условия (1) и
(2)
переформулировать на комбинаторном языке, то получится
определение 2.
Это комбинаторное определение несколько обобщается, если допустить в
матрице  повторяющиеся строки, что эквивалентно вероятностному
определению 1,
когда значения вероятностей
повторяющиеся строки, что эквивалентно вероятностному
определению 1,
когда значения вероятностей 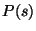 - рациональные числа.
- рациональные числа.
Пример 2. (продолжение)
Переформулируем данную выше конструкцию
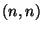 -пороговой СРС на комбинаторном языке. Строками матрицы
-пороговой СРС на комбинаторном языке. Строками матрицы  являются
все векторы
являются
все векторы  такие, что
такие, что
 . Очевидно, что
матрица
. Очевидно, что
матрица  задает совершенную комбинаторную СРС для
задает совершенную комбинаторную СРС для
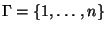 , так как для любого собственного
подмножества
, так как для любого собственного
подмножества
 и
любых заданных значений координат из множества
и
любых заданных значений координат из множества  число строк матрицы
число строк матрицы
 с данным значением нулевой координаты равно
с данным значением нулевой координаты равно 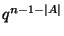 .
.
Удивительно, но простой схемы примера 2 оказывается
достаточно, чтобы из нее, как из кирпичиков, построить
совершенную СРС для произвольной структуры доступа. А
именно, для всех разрешенных множеств, т.е. для 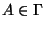 , независимо реализуем описанную только что
пороговую
, независимо реализуем описанную только что
пороговую  -СРС, послав тем самым
-СРС, послав тем самым  -му
участнику столько ``проекций''
-му
участнику столько ``проекций'' 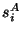 , скольким
разрешенным множествам он принадлежит. Это словесное
описание несложно перевести на комбинаторный язык свойств
матрицы
, скольким
разрешенным множествам он принадлежит. Это словесное
описание несложно перевести на комбинаторный язык свойств
матрицы  и убедиться, что эта СРС совершенна. Как это
часто бывает, ``совершенная'' не значит ``экономная'', и у
данной СРС размер ``проекции'' оказывается, как правило, во
много раз больше, чем размер секрета. Эту схему можно
сделать более экономной, так как достаточно реализовать
пороговые
и убедиться, что эта СРС совершенна. Как это
часто бывает, ``совершенная'' не значит ``экономная'', и у
данной СРС размер ``проекции'' оказывается, как правило, во
много раз больше, чем размер секрета. Эту схему можно
сделать более экономной, так как достаточно реализовать
пороговые  -СРС только для минимальных
разрешенных множеств
-СРС только для минимальных
разрешенных множеств  , т.е. для
, т.е. для
 ,
где
,
где 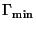 - совокупность минимальных
(относительно включения) множеств из
- совокупность минимальных
(относительно включения) множеств из  . Тем не
менее, для пороговой
. Тем не
менее, для пороговой  -СРС размер ``проекции''
(измеренный, например, в битах) будет в
-СРС размер ``проекции''
(измеренный, например, в битах) будет в
 раз больше размера секрета (это
наихудший случай для рассматриваемой конструкции). С другой
стороны, как мы убедимся чуть позже, любая пороговая
структура доступа может быть реализована идеально, т.е. при
совпадающих размерах ``проекции'' и секрета. Поэтому
естественно возникает вопрос о том, каково максимально
возможное превышение размера ``проекции'' над размером
секрета для наихудшей структуры доступа при наилучшей
реализации. Формально,
раз больше размера секрета (это
наихудший случай для рассматриваемой конструкции). С другой
стороны, как мы убедимся чуть позже, любая пороговая
структура доступа может быть реализована идеально, т.е. при
совпадающих размерах ``проекции'' и секрета. Поэтому
естественно возникает вопрос о том, каково максимально
возможное превышение размера ``проекции'' над размером
секрета для наихудшей структуры доступа при наилучшей
реализации. Формально,
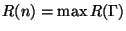 , где
, где  берется по всем структурам доступа
берется по всем структурам доступа  на
на  участниках, а
участниках, а
 , где
, где 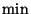 берется по всем СРС,
реализующим данную структуру доступа
берется по всем СРС,
реализующим данную структуру доступа  , а
, а  -
по
-
по 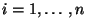 . Приведенная конструкция показывает, что
. Приведенная конструкция показывает, что
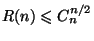 . С другой стороны, как было доказано
лишь недавно [5],
. С другой стороны, как было доказано
лишь недавно [5],
 . Такая огромная
``щель'' между верхней и нижней оценкой дает, по нашему
мнению, достаточный простор для исследований (автор
предполагает, что
. Такая огромная
``щель'' между верхней и нижней оценкой дает, по нашему
мнению, достаточный простор для исследований (автор
предполагает, что 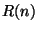 растет экспоненциально от
растет экспоненциально от  ).
).
Next: 5.3. Линейное разделение секрета
Up: 5. Математика разделения секрета
Previous: 5.1. Введение
Contents: Содержание