Next: 5.2. Разделение секрета для Up: 5. Математика разделения секрета Previous: 5. Математика разделения секрета Contents: Содержание

5.1. Введение

Рассмотрим следующую, в наше время вполне реальную ситуацию. Два совладельца драгоценности хотят положить ее на хранение в сейф. Сейф современный, с цифровым замком на 16 цифр. Так как совладельцы не доверяют друг другу, то они хотят закрыть сейф таким образом, чтобы они могли открыть его вместе, но никак не порознь. Для этого они приглашают третье лицо, называемое дилером, которому они оба доверяют (например, потому что оно не получит больше доступ к сейфу). Дилер случайно выбирает 16 цифр в качестве ``ключа'', чтобы закрыть сейф, и затем сообщает первому совладельцу втайне от второго первые 8 цифр ``ключа'', а второму совладельцу втайне от первого - последние 8 цифр ``ключа''. Такой способ представляется с точки здравого смысла оптимальным, ведь каждый из совладельцев получил ``полключа'' и что может быть лучше?! Недостатком данного примера является то, что любой из совладельцев, оставшись наедине с сейфом, может за пару минут найти недостающие ``полключа'' с помощью несложного устройства, перебирающего ключи со скоростью 1МГц. Кажется, что единственный выход - в увеличении размера ``ключа'', скажем, вдвое. Но есть другой, математический выход, опровергающий (в данном случае - к счастью) соображения здравого смысла. А именно, дилер независимо выбирает две случайные последовательности по 16 цифр в каждой, сообщает каждому из совладельцев втайне от другого ``его'' последовательность, а в качестве ``ключа'', чтобы закрыть сейф, использует последовательность, полученную сложением по модулю 10 соответствующих цифр двух выбранных последовательностей. Довольно очевидно (и ниже мы это докажем), что для каждого из совладельцев все 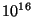возможных ``ключей'' одинаково вероятны и остается только перебирать их, что потребует в среднем более полутора лет для устройства, перебирающего ключи со скоростью 100МГц.

И с математической, и с практической точки зрения неинтересно останавливаться на случае двух участников и следует рассмотреть общую ситуацию. Неформально говоря, ``схема, разделяющая секрет'' (СРС) позволяет ``распределить'' секрет между участниками таким образом, чтобы заранее заданные разрешенные множества участников могли однозначно восстановить секрет (совокупность этих множеств называется структурой доступа), а неразрешенные - не получали никакой дополнительной к имеющейся априорной информации о возможном значении секрета. СРС с последним свойством называются совершенными (и только они, как правило, рассматриваются в этой статье).

История СРС начинается с 1979 года, когда эта проблема была поставлена и во многом решена Г. Блейкли [1] и А. Шамиром [2] для случая пороговых -СРС (т.е. разрешенными множествами являются любые множества из или более элементов). Особый интерес вызвали так называемые идеальные СРС, т.е. такие, где ``размер'' информации, предоставляемой участнику, не больше ``размера'' секрета (а меньше, как было показано, он и не может быть). Оказалось [3], что любой такой СРС соответствует матроид (определение, что это такое, см. в разделе 4) и, следовательно, не для любой структуры доступа возможно идеальное разделение секрета. С другой стороны, было показано, что для любого набора разрешенных множеств можно построить совершенную СРС, однако известные построения весьма ``неэкономны''. В данной статье рассматриваются алгебро-геометрические и комбинаторные задачи, возникающие при математическом анализе ``схем, разделяющих секрет''. Вот пример одной из таких задач.

Будем говорить, что семейство подпространств конечномерного векторного пространства 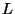над полем удовлетворяет свойству ``все или ничего'', если для любого множества линейная оболочка подпространств 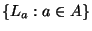либо содержит подпространство 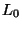целиком, либо пересекается с ним только по вектору 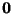. 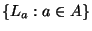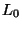В разделе 3 мы увидим, что такое семейство задает ``линейную'' СРС, у которой множество является разрешенным, если и только если линейная оболочка подпространств содержит подпространство целиком. В связи с этим понятием возникает ряд вопросов. Например, если поле конечно (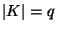) и все подпространства одномерны, то каково максимально возможное число участников для линейных пороговых -СРС (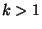)? Иначе говоря, каково максимально возможное число векторов 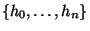таких, что любые векторов, содержащие вектор , линейно независимы, а любые 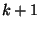векторов, содержащие вектор , линейно зависимы. 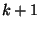Оказывается, что это свойство эквивалентно следующему, на первый взгляд более сильному, свойству: любые векторов линейно независимы, а любые  - линейно зависимы. Такие системы векторов изучались в геометрии как -множества () в конечной проективной геометрии 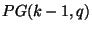, в комбинаторике как ортогональные таблицы силы  и индекса , в теории кодирования как проверочные матрицы МДР кодов (подробнее см. [4]). В разделе 3 мы приведем известную конструкцию таких множеств с 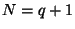, а довольно старая гипотеза состоит в том, что это и есть максимально возможное , за исключением двух случаев: случая , когда 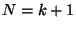, и случая 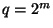, 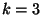или , когда

Next: 5.2. Разделение секрета для Up: 5. Математика разделения секрета Previous: 5. Математика разделения секрета Contents: Содержание