4.4. Как отличить составное число от простого

Данные ИИ Разработка Безопасность Инфраструктура Квантовые вычисления Курсы и книги

Next: 4.5. Как строить большие Up: 4. Алгоритмические проблемы теории Previous: 4.3. Сложность теоретико-числовых алгоритмов Contents: Содержание

4.4. Как отличить составное число от простого

Существует довольно эффективный способ убедиться, что заданное число является составным, не разлагая это число на множители. Согласно малой теореме Ферма, если число простое, то для любого целого , не делящегося на , выполняется сравнение

$\begin{displaymath} a^{N-1}\equiv1\pmod N. \end{displaymath}$ (9)

Если же при каком-то

это сравнение нарушается, можно утверждать, что

- составное. Проверка (9) не требует больших вычислений, это следует из алгоритма 1. Вопрос только в том, как найти для составного

целое число

, не удовлетворяющее (9). Можно, например, пытаться найти необходимое число

, испытывая все целые числа подряд, начиная с 2. Или попробовать выбирать эти числа случайным образом на отрезке

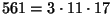К сожалению, такой подход не всегда дает то, что хотелось бы. Имеются составные числа , обладающие свойством (9) для любого целого с условием . Такие числа называются числами Кармайкла. Рассмотрим, например, число $561=3\cdot11\cdot17$ . Так как делится на каждое из чисел 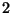, , , то с помощью малой теоремы Ферма легко проверить, что 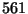есть число Кармайкла. 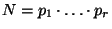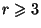Можно доказать (Carmichael, 1912), что любое из чисел Кармайкла имеет вид $N=p_1\cdot\ldots\cdot p_r$ , $r\geq3$ , где все простые различны, причем делится на каждую разность 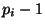. Лишь недавно, см. [10], была решена проблема о бесконечности множества таких чисел.

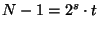В 1976 г. Миллер предложил заменить проверку (9) проверкой несколько иного условия. Детали последующего изложения можно найти в [8]. Если - простое число, $N-1=2^s\cdot t$ , где нечетно, то согласно малой теореме Ферма для каждого с условием хотя бы одна из скобок в произведении

$\begin{displaymath} (a^t-1)(a^t+1)(a^{2t}+1)\cdot\ldots\cdot(a^{2^{s-1}t}+1)= a^{N-1}-1 \end{displaymath}$

делится на

. Обращение этого свойства можно использовать, чтобы отличать составные числа от простых.

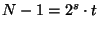Пусть - нечетное составное число, $N-1=2^s\cdot t$ , где нечетно. Назовем целое число , , ``хорошим'' для , если нарушается одно из двух условий:
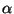$\alpha$ ) не делится на ;
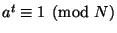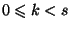$\beta$ ) $a^t\equiv1\pmod N$ или существует целое , $0\leq k<s$ , такое, что

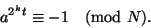
$\begin{displaymath} a^{2^kt}\equiv-1\pmod N. \end{displaymath}$

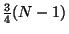Из сказанного ранее следует, что для простого числа не существует хороших чисел . Если же составное число, то, как доказал Рабин, их существует не менее $\frac{3}{4}(N-1)$ .