2008 г.
Обзор алгоритмов MOLAP
Юрий Кудрявцев, факультет ВМиК МГУ
Вперед: Многопозиционное агрегирование массивов для вычисления кубов
Выше: Синтаксические алгоритмы
Назад: Синтаксические алгоритмы
Содержание
Подразделы
Алгоритм DWARF (карлик) (см. [21]) назван так с намеком на звезды карликового типа,
которые имеют небольшой объем, но огромную массу. Это синтаксический
алгоритм, распознающий два типа избыточности хранения данных и
устраняющий их во время создания и поддержки куба.
Ключевыми понятиями алгоритма являются префиксная избыточность и
суффиксная избыточность (см. определения).
В пользу практического использования
алгоритма DWARF говорит автоматическое нахождение префиксных и
суффиксных избыточностей, не требующее каких-либо знаний о
распределении данных, типов, значений. При этом эффективность сжатия
одинаково высока как и для ''разреженных'', так и для
''плотных'' кубов. В большинстве случаев даже для очень плотных кубов размер
результирующего DWARF куба меньше размера базовой таблицы. Если для ''плотных'' кубов
улучшения происходят за счет префиксной
избыточности, то, по мере того как кубы становятся ''разреженнее'',
возрастает доля суффиксной избыточности.
Не менее важным является сокращение времени создания и расчетов.
Каждый избыточный суффикс идентифицируется до его вычисления, что
ведет к существенным уменьшениям времени создания. Более того,
вследствие уменьшения общего размера куба пропорционально падает и
время обработки запросов.
Определение 2.1
Префиксная избыточность.
Пусть имеется есть куб с измерениями a, b и с. Каждое значение
измерения a участвует в четырех группировках (a, ab, ac,
abc) и, возможно, много раз в каждой из сгруппированных
таблиц.
DWARF успешно распознает подобный тип изыбыточности и
устраняет его за счет хранения каждого префикса лишь
один раз.
Определение 2.2
Суффиксная избыточность
возникает, если 2 или более сгруппированные таблицы разделяют однаковый суффикс
(например, abc и bc).
Рассмотрим значение
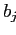
измерения
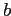
,
которое появляется в базовой таблице с единственным значением
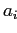
измерения
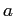
. Тогда сгруппированные таблицы
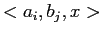
и
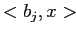
всегда
будут иметь одинаковые агрегирующие значения. Это происходит
благодаря тому, что вторая сгруппированная таблица агрегирует все
значения фактической таблицы, которые содержат все возможные
комбинации значений измерения
(в нашем случае это только значение
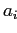
)
с
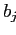
и
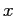
. Эта идея расширяет понятие базового единичного кортежа (BST, Base Single
Tuple)
(см.
определение) из алгоритма ''сжатого'' куба [
25].
Поскольку
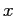
обычно является множеством значений,
суффиксная избыточность может иметь экспоненциальный эффект.
Суффиксная избыточность определяется во время создания DWARF-куба и
уничтожается за счет поглощения (или слияния) места, занимаемого избыточными суффиксами.
Таблица 5.1:
Копия таблицы 1.1
|
|
Для начала приведем пример структуры куба, а в дальнейшем дадим
формальное определение. Рисунок 2.1 показывает структуру куба для таблицы
1.1, в качестве агрегирующей функции используется SUM.
Вершины пронумерованы в порядке их создания. Высота куба равна числу
измерений, каждое из которых относится к одному из уровней, как показано
на рисунке.
Корневая вершина содержит ячейки вида {ключ, указатель} для
каждого значения первого измерения. Указатель каждой ячейки направлен к
лежащей ниже вершине, которая содержит все различные значения следующего измерения,
ассоциированные с ключом ячейки.
Каждая вершина содержит специальную ячейку ALL,
изображенную серой областью справа от вершины, содержащую указатель и отвечающую
всем значениям вершины. Каждый лист L имеет форму {ключ, агрегирующее значение} и
содержит агрегирующее значение всех кортежей, которые удовлетворяют пути (паттерну)
от корня к L. Каждый лист содержит и ALL ячейку, которая содержит агрегирующее
значение всех ячеек вершины.
На рисунке 2.1 все вершины, к которым идет более одного указателя, поглощают несколько путей (возможных вершин).
- Это ациклический ориентированный граф с одной корневой вершиной,
имеющий ровно D уровней, где D-число измерений.
- Вершины уровня D (листья) содержат ячейки вида {ключ,
агрегирующее значение}.
- Вершины на уровнях, отличных от уровня D, (нелистовых) содержат ячейки вида {ключ, указатель}.
Ячейка С в нелистовой вершине уровня i указывает на вершину уровня
i+1, которую она обобщает. С — родительская вершина для
обобщаемой вершины.
- В каждой вершине имеется специальная ячейка, которая содержит псевдо-значение ALL
как ключ. Эта ячейка содержит указатель или на нелистовую вершину, или на
агрегирующее значение листовой вершины.
- Ячейки на i-ом уровне содержат ключи, являющиеся значениями i-того
измерения куба. Внутри одной вершины не может встречаться повторения ключа.
- Каждая ячейка
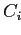 на i-ом уровне структуры отвечает последовательности
на i-ом уровне структуры отвечает последовательности 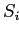 из i ключей, входящих в путь от корня до ячейки. Такой путь соответствует
оператору group by с (D-i) не указанными измерениями. Все группировки, содержащие
из i ключей, входящих в путь от корня до ячейки. Такой путь соответствует
оператору group by с (D-i) не указанными измерениями. Все группировки, содержащие
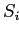 в качестве префикса, будут относиться к ячейкам, являющимся потомками
в качестве префикса, будут относиться к ячейкам, являющимся потомками
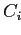 в структуре куба. Для всех подобных группировок их общий префикс будет
хранится единожды.
в структуре куба. Для всех подобных группировок их общий префикс будет
хранится единожды.
- Когда две или более группировки создают одинаковые вершины и ячейки,
их хранение обобщается (поглощается), чтобы можно было хранить только одну
копию. В таком случае результирующая вершина будет достижима более
чем одним путем из корня, причем все пути будут иметь одинаковый
суффикс. Если вершина N — обобщающая, то все ее потомки будут обобщающими вершинами.
- Точечные запросы
- выполняются последовательным разыменованием пути в структуре куба.
Таким образом, этот вид запросов выполняется намного быстрее, чем в аналогичных алгоритмах
или базовых таблицах, за счет того, что для каждого запроса требуется ровно D обращений к вершинам
куба, где D — число измерений (уровней) куба.
- Интервальные запросы
- включают хотя бы одно измерение с интервалом значений. Для
каждого из ключей i-ого уровня, попадающего в интервал, строятся рекурсивные подзапросы к
нижележащим подкубам, что тоже достаточно просто по структуре.
- Обратные запросы
- оптимизаций по выполнению обратных запросов этот алгоритм не дает,
но возможно его сочетание с какими-либо другими алгоритмами, ориентированными на обратные запросы.
Правда, в настоящее время все оптимизации обратных запросов основаны на специально создаваемых кубах,
поэтому такое объединение алгоритмов — нетривиальная задача. См.
также Алгоритм Bottom-Up Computation.
Сложность
Несмотря на то, что показана NP-полнота общей задачи выбора
представлений для материализации [
10], в работе
[
22] были даны новые оценки сложности
алгоритма DWARF. Большая часть этих результатов вошла в данный
раздел. При этом хотелось бы в очередной раз подчеркнуть, что
DWARF — алгоритм полной материализации (materialize-all). Также
хотелось бы отметить, что оценки в работе
[
22] были получены при наложении определенных
условий на начальные данные.
С помощью приведенной ниже модели можно показать, что вычислительная
сложность алгоритма и объем результирующего куба равны:
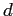 — число измерений
— число измерений
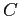 — мощность измерения
— мощность измерения
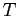 — число фактических кортежей
— число фактических кортежей
Приведем некие трактовки данного результата.
Модель опирается
на понятия префиксной, суффиксной избыточности, приведенные выше в
описании алгоритма (см.
определения).
Разобьем категории сжатия на две группы:
- сжатие разреженности (sparsity coalescing)
- сжатие связанности (implication coalescing)
Введем категории сжатия разреженности.
Хвостовое сжатие (Tail Coalescing) происходит на всех группировках,
имеющих префикс
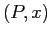
, где
- путь
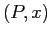 ведет к подкубу, агрегирующему только один
фактический кортеж (см. также случай базового единичного кортежа (BST);
ведет к подкубу, агрегирующему только один
фактический кортеж (см. также случай базового единичного кортежа (BST);
- путь
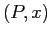 не проходит ни через один
указатель .
не проходит ни через один
указатель .
Левое сжатие (Left Coalescing) происходит на всех группировках,
имеющих общий префикс 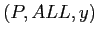 , где
, где
- путь
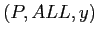 ведет к подкубу, агрегирующему только один
фактический кортеж;
ведет к подкубу, агрегирующему только один
фактический кортеж;
- путь
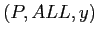 проходит хотя бы через один указатель ALL.
Области куба, агрегирующие только один фактический кортеж, создают большую
избыточность структуры. Ниже будет показано, что избавление от избыточности
разреженности приводит к почти полиномиальному времени создания куба.
проходит хотя бы через один указатель ALL.
Области куба, агрегирующие только один фактический кортеж, создают большую
избыточность структуры. Ниже будет показано, что избавление от избыточности
разреженности приводит к почти полиномиальному времени создания куба.
Примеры категорий сжатия разреженности:
Рис. 2.2:
Категории сжатия разреженности
|
|
Сжатие разреженности работает только на тех областях куба, где
существует только один фактический кортеж. В свою очередь, сжатие
связанности расширяет данный метод путем сжатия на подкубах.
Например, для таблицы 1.1 из введения продукт ''еда'' продается только
осенью.
Сжатие связанности, таким образом, представляет
собой расширение понятия левого сжатия на случай наличия связей
(implications) между значениями измерений. Подобные связи часто наблюдаются в
реальных базах данных.
Авторы опускают необходимую при
создании DWARF-куба лексикографическую сортировку начальной
таблицы (во время создания куба появление нового префикса
означает необходимость создания новой вершины на уровне, где различаются
префиксы). Сортировка всей фактической таблицы —
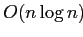 или
или 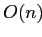 в лучшем случае (сортировка слиянием, кучами или подсчетом, вычерпыванием). Но
с учетом NP-полноты начальной задачи, этим затратами можно пренебречь.
в лучшем случае (сортировка слиянием, кучами или подсчетом, вычерпыванием). Но
с учетом NP-полноты начальной задачи, этим затратами можно пренебречь.
Пусть существует таблица фактических данных с 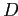 измерениями
(
измерениями
(
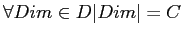 ), и количество фактических кортежей
), и количество фактических кортежей
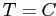 . Не нарушая общности, положим
. Не нарушая общности, положим
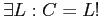 .
У получившегося сжатого куба (или DWARF-куба) корневая ячейка будет иметь вид,
показанный на рисунке 2.4. Группа
.
У получившегося сжатого куба (или DWARF-куба) корневая ячейка будет иметь вид,
показанный на рисунке 2.4. Группа 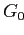 содержит ячейки, не имеющие связи с фактическими кортежами, группа
содержит ячейки, не имеющие связи с фактическими кортежами, группа
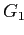 — ячейки, связанные с одним кортежем фактической таблицы,
— ячейки, связанные с одним кортежем фактической таблицы, 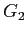 — два
фактических кортежа.
— два
фактических кортежа.
Лемма 1
Если из набора равномерно распределенных 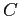 элементов выбрать некоторый элемент и повторить выбор
элементов выбрать некоторый элемент и повторить выбор 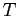 раз, то вероятность выбора этого
элемента ровно
раз, то вероятность выбора этого
элемента ровно 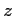 раз приблизительно равна:
раз приблизительно равна:
Равномерность — еще одно ограничение на входные фактические
данные.
В общем случае:
Коротко укажем дальнейшие пункты доказательства.
Применяя лемму 1 к группам 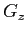 и подставляя
и подставляя 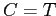 ,
получим
,
получим
Лемма 2
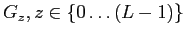 содержит
содержит
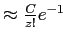 ячеек, которые адресуют ровно
ячеек, которые адресуют ровно 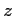 кортежей.
кортежей.
В общем случае в 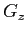 попадает
попадает
В случае неравномерного распределения кортежей, данная сумма
будет отличаться от результатов [22], и это
повлечет изменение всех дальнейших оценок в леммах.
Лемма 3
Число дубликатных ключей в вершине, на которую указывает ячейка группы 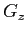 ,
равно 0. (
,
равно 0. (
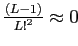 )
)
Основываясь на введенных выше понятиях левого и хвостового сжатий,
можно показать, что
и
Здесь 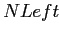 — число ячеек, подвергающихся левому сжатию, и
— число ячеек, подвергающихся левому сжатию, и
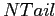 — число ячеек, подвергающихся хвостовому сжатию.
— число ячеек, подвергающихся хвостовому сжатию.
Из последней формулы получим следующее соотношение для числа ячеек куба:
А поскольку при устранении суффиксной избыточности DWARF, в отличие от других алгоритмов,
проверяет каждую ячейку только один раз
(автору неизвестны алгоритмы, которые для устранения суффиксной избыточности не проверяли бы каждую
ячейку экспоненциальное число раз), получаем ту же оценку и для сложности работы
алгоритма.
При использовании этого алгоритма структура куба сжимается синтаксически.
Префиксная и суффиксная избыточности устраняются за счет создания лучшей системы
адресации и хранения ячеек. Алгоритмы, предложенные для создания и модификации кубов
с использованием данной структуры, являются наилучшими из всех синтаксических решений
на данный момент. Таким образом, если не рассматривать различные эвристические алгоритмы
или более глубоких семантические изменения, то в настояющее время этот синтаксический алгоритм или его различные
(правда уже частично эвристические) модификации
являются оптимальными для хранения и адресации OLAP — данных.
Вперед: Многопозиционное агрегирование массивов для вычисления кубов
Выше: Синтаксические алгоритмы
Назад: Синтаксические алгоритмы
Содержание