2008 г.
Обзор алгоритмов MOLAP
Юрий Кудрявцев, факультет ВМиК МГУ
Вперед: Алгоритм Star-Cubing
Выше: Вычисление Iceberg кубов
Назад: Вычисление Iceberg кубов
Содержание
Алгоритм Bottom-Up Computation
BUC-алгоритм предназначен для вычисления разреженных кубов и кубов типа айсберг. При этом, в отличие от MultiWay, куб рассчитывается от наиболее общего подкуба к детальным подкубам. Поэтому можно снизить затраты на партиционирование данных. К тому же подобный порядок позволяет наиболее эффективно использовать условие Apriori, снижая объем необходимых вычислений.
Bottom-Up Computation переводится как вычисление "снизу вверх", что вызывает недоумение, т.к. структуры кубов принято изображать, располагая детальные подкубы ниже, а агрегирующие выше. С этим связаны и термины roll-up и drill-down: мы или поднимаемся выше по структуре, агрегируя данные (roll-up), либо спускаемся к детальным элементам (drill-down). Однако авторы работы [4], использовали противоположный подход, и название алгоритма закрепилось.
На рисунке 4.1 изображена схема работы алогоритма BUC для создания трехмерного куба ABC, с измерениями A, B и С.
В общих чертах, алгоритм работает следующим образом:
- Агрегируется весь набор входных данных и записывается итоговый результат.
- Для каждого измерения d входные данные партиционируются по d, т.е. для каждого уникального элемента d создается партиция.
- Для каждой партиции, созданной на предыдущем шаге, проверяется условие MinSup. К примеру, если задано условие count > x, то проверяется количество кортежей в партиции.
- Если партиция удовлетворяет условию MinSup, то рекурсивно запускается алгоритм BUC, и в качестве входных данных используется эта партиция. Таким образом вычисляется куб типа айсберг по измерениям, начиная от d+1.
- После возвращения из вложенных рекурсивных вызовов на партициях по измерению d, алгоритм повторяется для следующего измерения.
Рассмотрим работу алгоритма на примере создания четырехмерного куба с измерениями A, B, C и D и условием MinSup "count > 3". Предположим, что измерение А содержит 4 элемента
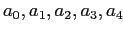 , измерение B - 4 элемента
, измерение B - 4 элемента
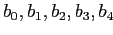 , измерение C - 2 элемента
, измерение C - 2 элемента 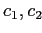 и измерение D - 2 элемента
и измерение D - 2 элемента 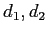 . Поскольку каждый подкуб является партцией, то в соответствии с условием MinSup нам необходимо вычислить все подкубы, агрегирующие более трех кортежей.
. Поскольку каждый подкуб является партцией, то в соответствии с условием MinSup нам необходимо вычислить все подкубы, агрегирующие более трех кортежей.
Рисунок 4.1 показывает порядок партиционирования исходных данных по различным элементам измерения А, затем В, С и D. Для этого BUC сканирует исходные данные, агрегируя все кортежи, чтобы получить итоговое значение all. Партиционирование по измерению А создает 4 партиции, при этом запоминается количество кортежей в каждой партиции.
Рис. 4.1:
Разбиение данных при работе алгоритма BUC
|
|
Использование условия Appriori позволяет сократить время работы алгоритма. Начиная с элемента 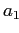 измерения A, кортежи партиции
измерения A, кортежи партиции 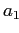 агрегируются с вычислением значения
агрегируются с вычислением значения
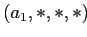 . Предположим, что
. Предположим, что
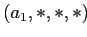 удовлетворяет условию MinSup, тогда запускается рекурсивное вычисление для партиции
удовлетворяет условию MinSup, тогда запускается рекурсивное вычисление для партиции
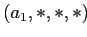 .
.
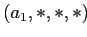 партиционируется по измерению В. Проверяется количество кортежей для
партиционируется по измерению В. Проверяется количество кортежей для
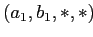 . Если для
. Если для
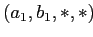 условие MinSup удовлетворяется, то партиционирование продолжается по C, начиная с
условие MinSup удовлетворяется, то партиционирование продолжается по C, начиная с 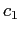 . Если же в
. Если же в
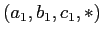 количество исходных фактов равно 2, что не удовлетворяет исходному условию MinSup , то по лемме Apriori и ни один из потомков не будет удовлетворять условию MinSup. В этом случае алгоритм BUC не вычисляет дальше
количество исходных фактов равно 2, что не удовлетворяет исходному условию MinSup , то по лемме Apriori и ни один из потомков не будет удовлетворять условию MinSup. В этом случае алгоритм BUC не вычисляет дальше
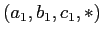 , избегая затрат на партиционирование по измерению D. Вычисляется
, избегая затрат на партиционирование по измерению D. Вычисляется
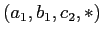 и так далее.
и так далее.
Производительность алгоритма BUC зависит от порядка измерений и симметричности данных. Измерения должны обрабатываться в порядке убывания мощности (количества элементов). Чем больше мощность измерения, тем меньше партиции и больше вариантов для применения условия MinSup. Аналогично, равномерные измерения (когда данные равномерно распределены по элементам) лучше подходят для применения условия Apriori.
Основным достоинством алгоритма BUC можно считать эффективное распределение затрат на партиционирование. Однако, в отличие от MultiWay, расходы на агрегирование не разделяются между родителями и потомками. К примеру, результаты вычисления подкуба AB не используются для вычисления подкуба ABC, который нужно вычислять с нуля.
Вперед: Алгоритм Star-Cubing
Выше: Вычисление Iceberg кубов
Назад: Вычисление Iceberg кубов
Содержание