4.1. Введение
Вопрос ``как сосчитать?'' всегда сопутствовал теоретико-числовым исследованиям. Труды Евклида и Диофанта, Ферма и Эйлера, Гаусса, Чебышева и Эрмита содержат остроумные и весьма эффективные алгоритмы решения диофантовых уравнений, выяснения разрешимости сравнений, построения больших по тем временам простых чисел, нахождения наилучших приближений и т.д. Без преувеличения можно сказать, что вся теория чисел пронизана алгоритмами. В последние два десятилетия, благодаря в первую очередь запросам криптографии и широкому распространению ЭВМ, исследования по алгоритмическим вопросам теории чисел переживают период бурного и весьма плодотворного развития. Мы кратко затронем здесь лишь те алгоритмические аспекты теории чисел, которые связаны с криптографическими применениями.
Вычислительные машины и электронные средства связи проникли практически во все сферы человеческой деятельности. Немыслима без них и современная криптография. Шифрование и дешифрование текстов можно представлять себе как процессы переработки целых чисел при помощи ЭВМ, а способы, которыми выполняются эти операции, как некоторые функции, определенные на множестве целых чисел. Все это делает естественным появление в криптографии методов теории чисел. Кроме того, стойкость ряда современных криптосистем обосновывается только сложностью некоторых теоретико-числовых задач (см. [22]).
Но возможности ЭВМ имеют определенные границы. Приходится
разбивать длинную цифровую последовательность на блоки ограниченной длины
и шифровать каждый такой блок отдельно. Мы будем считать в дальнейшем, что
все шифруемые целые числа неотрицательны и по величине меньше некоторого
заданного (скажем, техническими ограничениями) числа 
. Таким же условиям
будут удовлетворять и числа, получаемые в процессе шифрования. Это позволяет
считать и те, и другие числа элементами кольца вычетов 
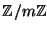. Шифрующая
функция при этом может рассматриваться как взаимнооднозначное отображение
колец вычетов
а число
представляет собой сообщение 
в зашифрованном виде.
Простейший шифр такого рода - шифр замены, соответствует
отображению
при некотором фиксированном
целом 
. Подобный шифр использовал еще Юлий Цезарь. Конечно, не
каждое отображение 
подходит для целей надежного сокрытия информации
(подробнее об этом см. главу 1).
В 1978 г., см. [1], американцы Р.Ривест, А.Шамир и Л.Адлеман
(R.L.Rivest, A.Shamir, L.Adleman) предложили пример функции ,
обладающей рядом замечательных достоинств. На ее основе была построена
реально используемая система шифрования, получившая название по первым
буквам имен авторов - система RSA. Эта функция такова, что
а) существует достаточно быстрый алгоритм вычисления значений ;
б) существует достаточно быстрый алгоритм вычисления значений
обратной функции 
;
в) функция обладает некоторым ``секретом'', знание которого
позволяет быстро вычислять значения ;
в противном же случае вычисление
становится трудно разрешимой в вычислительном отношении задачей,
требующей для своего решения столь много времени, что по его прошествии
зашифрованная информация перестает представлять интерес для лиц,
использующих отображение в качестве шифра.
Подробнее об отображениях такого сорта и возможностях их использования в криптографии рассказано в главах 1, 2.
Еще до выхода из печати статьи [1] копия доклада в Массачусетсском Технологическом институте, посвященного системе RSA, была послана известному популяризатору математики М. Гарднеру, который в 1977 г. в журнале Scientific American опубликовал статью [2], посвященную этой системе шифрования. В русском переводе заглавие статьи Гарднера звучит так: Новый вид шифра, на расшифровку которого потребуются миллионы лет. Именно статья [2] сыграла важнейшую роль в распространении информации об RSA, привлекла к криптографии внимание широких кругов неспециалистов и фактически способствовала бурному прогрессу этой области, произошедшему в последовавшие 20 лет.
Next: 4.2. Система шифрования RSA
Up: 4. Алгоритмические проблемы теории
Previous: 4. Алгоритмические проблемы теории
Contents: Содержание