Next: 7. Чистые и смешанные
Up: Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ
Previous: 5. Оценка секретных систем
Contents: Содержание
6. Алгебра секретных систем
Если имеются две секретные системы  и
и  , их часто можно
комбинировать различными способами для получения новой
секретной системы
, их часто можно
комбинировать различными способами для получения новой
секретной системы  . Если
. Если  и
и  имеют одну и ту же область
(пространство сообщений), то можно образовать своего рода
``взвешенную сумму''
имеют одну и ту же область
(пространство сообщений), то можно образовать своего рода
``взвешенную сумму''

где

. Эта операция состоит, во-первых, из
предварительного выбора систем

или

с вероятностями

и

. Этот
выбор является частью ключа

. После того как этот выбор
сделан, системы

или

применяются в соответствии с их
определениями. Полный ключ

должен указывать, какая из
систем

или

выбрана и с каким ключом используется выбранная
система.
Если  состоит из отображений
состоит из отображений
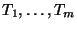 с
вероятностями
с
вероятностями 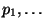
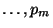 , а
, а  -- из
-- из 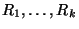 с
вероятностями
с
вероятностями 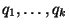 , то система
, то система
 состоит из отображений
состоит из отображений
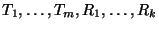 с вероятностями
с вероятностями

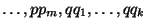 соответственно.
соответственно.
Обобщая далее, можно образовать сумму нескольких систем
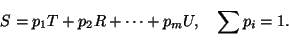
Заметим, что любая система

может быть записана как сумма
фиксированных операций

где

-- определенная операция шифрования в системе

,
соответствующая выбору ключа

, причем вероятность такого
выбора равна

.
Второй способ комбинирования двух секретных систем
заключается в образовании ``произведения'', как показано
схематически на рис. 3. Предположим, что  и
и  -- такие
две системы, что область определения (пространство языка)
системы
-- такие
две системы, что область определения (пространство языка)
системы  может быть отождествлена с областью определения
(пространством криптограмм) системы
может быть отождествлена с областью определения
(пространством криптограмм) системы  . Тогда можно применить
сначала систему
. Тогда можно применить
сначала систему  к нашему языку, а затем систему
к нашему языку, а затем систему  к результату
этой операции, что дает результирующую операцию
к результату
этой операции, что дает результирующую операцию  , которую
запишем в виде произведения
, которую
запишем в виде произведения

Ключ системы

состоит как из ключа системы

, так и из ключа
системы

, причем предполагается, что эти ключи выбираются
соответственно их первоначальным вероятностям и независимо.
Рис. 3.
Произведение двух систем S = RT.
|
Таким образом, если

ключей системы

выбирается с вероятностями

а

ключей системы

имеют вероятности

то система

имеет самое большее

ключей с вероятностями

. Во многих случаях некоторые из отображений

будут
одинаковыми и могут быть сгруппированы вместе, а их
вероятности при этом сложатся.
Произведение шифров используется часто; например, после
подстановки применяют транспозицию или после транспозиции -- код
Виженера; или же применяют код к тексту и зашифровывают
результат с помощью подстановки, транспозиции, дробным шифром и
т.д.
Можно заметить, что такое умножение, вообще говоря,
некоммутативно (т. е. не всегда 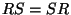 ), хотя в частных
случаях (таких, как подстановка и транспозиция)
коммутативность имеет место. Так как наше умножение
представляет собой некоторую операцию, оно по определению
ассоциативно, т. е.
), хотя в частных
случаях (таких, как подстановка и транспозиция)
коммутативность имеет место. Так как наше умножение
представляет собой некоторую операцию, оно по определению
ассоциативно, т. е.
 . Кроме того, верны
законы
. Кроме того, верны
законы

(взвешенный ассоциативный закон для сложения);

(право- и левосторонние дистрибутивные законы), а также
справедливо равенство
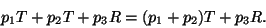
Следует подчеркнуть, что эти операции комбинирования сложения
и умножения применяются к секретным системам в целом.
Произведение двух систем 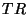 не следует смешивать с
произведением отображений в системах
не следует смешивать с
произведением отображений в системах 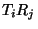 , которое также часто
используется в настоящей работе. Первое является секретной
системой, т.е. множеством отображений с соответствующими
вероятностями; второе -- является фиксированным отображением.
Далее, в то время как сумма двух систем
, которое также часто
используется в настоящей работе. Первое является секретной
системой, т.е. множеством отображений с соответствующими
вероятностями; второе -- является фиксированным отображением.
Далее, в то время как сумма двух систем  является
системой, сумма двух отображений не определена. Системы
является
системой, сумма двух отображений не определена. Системы  и
и  могут коммутировать, в то время как конкретные
могут коммутировать, в то время как конкретные  и
и  не коммутируют. Например, если
не коммутируют. Например, если  -- система Бофора
данного периода, все ключи которой равновероятны, то, вообще говоря,
-- система Бофора
данного периода, все ключи которой равновероятны, то, вообще говоря,

но, конечно, произведение

не зависит от порядка сомножителей;
действительно
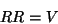
является системой Виженера того же самого периода со случайным
ключом. С другой стороны, если отдельные отображения

и

двух систем

и

коммутируют, то и системы
коммутируют.
Системы, у которых
пространства  и
и 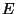 можно отождествить
(этот случай является очень частым, если последовательности букв
преобразуются в последовательности букв), могут быть названы
эндоморфными. Эндоморфная система
можно отождествить
(этот случай является очень частым, если последовательности букв
преобразуются в последовательности букв), могут быть названы
эндоморфными. Эндоморфная система  может быть
возведена в степень
может быть
возведена в степень 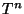 .
.
Секретная система  ,
произведение которой на саму себя равно
,
произведение которой на саму себя равно
 , т.е. такая, что
, т.е. такая, что
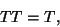
будет называться
идемпотентной. Например, простая подстановка,
транспозиция с периодом

, система Виженера с периодом

(все с
равновероятными ключами) являются идемпотентными.
Множество всех
эндоморфных секретных систем, определенных в
фиксированном пространстве сообщений, образует ``алгебраическую
систему'', т.е. некоторый вид алгебры, использующей операции
сложения и умножения. Действительно, рассмотренные свойства
сложения и умножения можно резюмировать следующим образом.
Множество
эндоморфных шифров с одним и тем же пространством
сообщений и двумя операциями комбинирования -- операцией
взвешенного сложения и операцией умножения -- образуют линейную
ассоциативную алгебру с единицей, с той лишь особенностью, что
коэффициенты во взвешенном сложении должны быть
неотрицательными, а их сумма должна равняться единице.
Эти операции комбинирования дают способы конструирования
многих новых типов секретных систем из определенных данных
систем, как это было показано в приведенных примерах. Их можно
также использовать для описания ситуации, с которой сталкивается
шифровальщик противника, когда он пытается расшифровать
криптограмму неизвестного типа. Фактически он расшифровывает
секретную систему типа

где
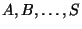
в данном случае -- известные типы шифров с их
априорными вероятностями

, а

соответствует возможности
использования совершенно нового неизвестного шифра.
Next: 7. Чистые и смешанные
Up: Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ
Previous: 5. Оценка секретных систем
Contents: Содержание