...к задачам девятой олимпиады

Next: Литература к главе 7 Up: 7.6. Указания и решения Previous: ...к задачам восьмой олимпиады Contents: Содержание

...к задачам девятой олимпиады

9.1. а) Для доказательства достаточно указать хотя бы одну последовательность из 33 различных букв, сумма которой с русским алфавитом из 33 букв не содержит одинаковых букв. В качестве искомой последовательности возьмем сам алфавит. Докажем, что сумма алфавита с самим собой не содержит одинаковых букв. Пусть и - порядковые номера различных букв алфавита. Тогда по определению сложения букв достаточно показать, что числа и имеют разные остатки от деления на 33. В самом деле, если бы они были одинаковы, то число делилось бы на 33 без остатка. 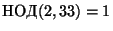В силу того что $\mathrm{НОД}(2, 33)=1$ , разность 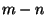также делилась бы на 33 без остатка, что невозможно. Утверждение пункта а) доказано.

Замечание. Утверждение пункта а) остается в силе для любого алфавита из нечетного числа букв.

б) При сложении двух последовательностей сумма порядковых номеров всех букв получаемой при этом последовательности и сумма порядковых номеров всех букв обоих слагаемых имеет один и тот же остаток от деления на 26. Значит, разность упомянутых сумм должна делиться на 26 без остатка. Докажем утверждение пункта б) методом от противного. В самом деле, если такая последовательность из 26 различных букв существует, то упомянутая разность равна сумме порядковых номеров букв алфавита. Однако сумма 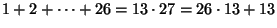$1+2+\dots+26=13\cdot27=26\cdot13+13$ при делении на 26 имеет остаток 13. Это доказывает утверждение пункта б).

Замечание. Утверждение пункта б) остается в силе для любого алфавита из четного числа букв.

Представляет интерес доказательство пункта б), предложенноеучастниками олимпиады.

При делении на любое четное число суммы двух четных или двух нечетных чисел получается четный остаток, а при делении суммы четного и нечетного чисел - нечетный остаток.

Соответствующие буквы складываемых последовательностей могут быть как одинаковой, так и различной четности. (Для краткости мы называем букву четной, если ее номер четен, и нечетной - если номер нечетен.) Будем решать задачу от противного. Предположим, что требуемая последовательность существует. Всего в сложении участвуют 52 буквы. Пар букв одинаковой и различной четности должно быть одинаковое количество, а именно 13 (так как в результате сложения должно получиться 13 четных и 13 нечетных букв). Пары букв различной четности включают в себя 26 букв. Оставшиеся 26 букв входят в 13 пар букв одинаковой четности. Однако, 13 пар букв одинаковой четности не могут содержать одинаковое количество четных и нечетных букв (так как 13 - нечетное число). Полученное противоречие доказывает утверждение пункта б).

9.2. В этой задаче условимся писать 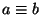$a\equiv b$ , если числа и имеют одинаковые остатки при делении на 33. Пусть - номер первой буквы искомой последовательности. Эту букву указанное число раз прибавили к букве К, в результате получили букву А. Запишем соответствующее уравнение:

$\begin{displaymath} 12+1949^{1999}\cdot n \equiv1. \end{displaymath}$ (1)

Имеем следующую цепочку соотношений:

$\begin{displaymath} 1949^{1999}\equiv 2^{5\cdot399+4}\equiv(-1)^{399}\cdot16\equiv -16\equiv 17. \end{displaymath}$

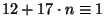
Уравнение (1) принимает вид: $12+17\cdot n \equiv1$ , или

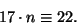$\begin{displaymath} 17\cdot n\equiv 22. \end{displaymath}$

(2)

Пользуясь арифметикой остатков, несложно составить следующую таблицу

А	Б	В	Г	Д	Е	$\myYott$	Ж	З	И	Й	К	Л	М	Н	О	П	Р	С	Т	У	Ф
17	1	18	2	19	3	20	4	21	5	22	6	23	7	24	8	25	9	26	10	27	11

Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
28	12	29	13	30	14	31	15	32	16	0

Здесь под каждой буквой подписан остаток от деления на 33 результата умножения ее номера на 17. Как видно из таблицы, уравнение (