Методы добычи данных при построении локальной метрики в системах вывода по прецедентам

Л. Е. Карпов, В. Н. Юдин
Препринт ИСП РАН

Назад   Оглавление   Вперёд

3. Добыча данных в системах поддержки принятия решений и прогнозирования

Русскоязычному термину "добыча данных" или "раскопка данных" в английском языке соответствует термин Data Mining. Нередко встречаются слова "обнаружение знаний в базах данных" (Knowledge Discovery in Databases) и "интеллектуальный анализ данных" (ИАД). Возникновение всех указанных терминов связано с новым витком в развитии средств и методов обработки данных. Цель добычи данных состоит в выявлении скрытых правил и закономерностей в наборах данных. Дело в том, что человеческий разум сам по себе не приспособлен для восприятия больших массивов разнородной информации. Человек обычно не способен улавливать более двух-трех взаимосвязей даже в небольших выборках. Но и традиционная математическая статистика, долгое время претендовавшая на роль основного инструмента анализа данных, также нередко пасует при решении задач из реальной сложной жизни. Она оперирует усредненными характеристиками выборки, которые часто являются фиктивными величинами (типа средней температуры пациентов по больнице, средней высоты дома на улице, состоящей из дворцов и лачуг и т. п.). Поэтому методы математической статистики оказываются полезными главным образом для проверки заранее сформулированных гипотез и для "грубого" разведочного анализа, составляющего основу оперативной аналитической обработки данных (online analytical processing – OLAP).

В основу современной технологии добычи данных положена концепция шаблонов (паттернов), отражающих фрагменты многоаспектных взаимоотношений в данных. Эти шаблоны представляют собой закономерности, свойственные подвыборкам данных, которые могут быть компактно выражены в понятной человеку форме. Поиск шаблонов производится методами, не ограниченными рамками априорных предположений о структуре выборки и виде распределений значений анализируемых показателей.

К задачам, использующим методы добычи данных, обычно относятся задачи, при решении которых требуется получить ответы, например, на следующие вопросы:

1. Какие факторы лучше всего предсказывают несчастные случаи (встречаются ли точные шаблоны в описаниях людей, подверженных повышенному травматизму)?
2. Какие характеристики отличают клиентов, которые, по всей вероятности, собираются отказаться от услуг телефонной компании?
3. Какие схемы покупок характерны для мошенничества с кредитными карточками?

Важное положение – нетривиальность разыскиваемых шаблонов. Это означает, что найденные шаблоны должны отражать неочевидные, неожиданные регулярности в данных, составляющие так называемые скрытые знания. К обществу пришло понимание того, что сырые (первичные) данные содержат глубинный пласт знаний, при грамотной раскопке которого могут быть обнаружены настоящие самородки.

В целом технологию добычи данных достаточно точно определяет Григорий Пиатецкий-Шапиро [Fayyad 96] – один из основателей этого направления. Добыча данных – это процесс обнаружения в сырых данных:

• ранее неизвестных;
• нетривиальных;
• практически полезных;
• доступных интерпретации знаний, необходимых для принятия решений в различных сферах человеческой деятельности.

3.1. Различные подходы к классификации области добычи данных

Существуют различные подходы к классификации самой области добычи данных. В частности, выделяют "дескриптивный" и "предиктивный" подход. Отличие этих двух подходов друг от друга заключается в том, что в первом случае мы обнаруживаем знания описательного характера, а во втором – знания, которые можно использовать для прогноза. В литературе встречаются также термины "структурный" и "неструктурный" подход. Такая терминология исходит из того, что предметом анализа могут быть как хорошо структурированные данные, например, таблицы в реляционной базе, так и неструктурированные данные, например, текст или изображения. "Исторический" подход основывается на том, что существует целый ряд исторически сложившихся дисциплин, например, теория нейронных сетей или нечеткая логика, перечисляя которые, определяют предмет и границы области добычи данных. Мы, следуя уже сложившейся в литературе традиции, будем придерживаться более формального подхода, а именно, называть все технологии добычи данных машинным обучением и делить их на две большие группы: "управляемое" и "неуправляемое" обучение.

В первом случае – "обучении с учителем" – задача анализа данных, например, классификация, осуществляется в несколько этапов. Сначала с помощью какого-либо алгоритма строится модель анализируемых данных – классификатор. Затем, этот классификатор подвергается "обучению". Другими словами, проверяется качество его работы и, если оно неудовлетворительно, происходит "дополнительное обучение" классификатора. Этот процесс повторяется до тех пор, пока не будет достигнут требуемый уровень качества и не возникнет убеждение, что выбранный алгоритм работает корректно с данными, либо же сами данные не имеют структуры, которую можно выявить.

Неуправляемое обучение объединяет технологии, выявляющие дескриптивные модели, например, закономерности, проявляющиеся при покупках, совершаемых клиентами большого магазина. Очевидно, что если эти закономерности есть, то модель должна их представить, и неуместно говорить об ее обучении. Отсюда и название – неуправляемое обучение. Дальнейшая классификация технологий добычи данных опирается на то, какие задачи этими технологиями решаются. Управляемое обучение, таким образом, подразделяется на классификацию и регрессию, а неуправляемое обучение – на анализ рыночных корзин, анализ временных последовательностей (секвенциальный анализ) и кластеризацию.

3.2. Классификация задач добычи данных

Целью технологии добычи данных является производство нового знания, которое пользователь может в дальнейшем применить для улучшения результатов своей деятельности. Рассмотрим основные виды моделей, которые используются для нахождения нового знания. Результат моделирования – это выявленные отношения в данных. Можно выделить, по крайней мере, семь методов выявления и анализа знаний:

1. классификация,
2. регрессия,
3. кластеризация,
4. анализ ассоциаций,
5. прогнозирование временных последовательностей (рядов),
6. агрегирование (обобщение),
7. обнаружение отклонений.

Методы 1, 2 и 4 используются, главным образом, для предсказания, в то время как остальные удобны для описания существующих закономерностей в данных.

Вероятно, наиболее распространенной сегодня операцией интеллектуального анализа данных является классификация. С ее помощью выявляются признаки, характеризующие группу, к которой принадлежит тот или иной объект. Это делается посредством анализа уже классифицированных объектов и формулирования некоторого набора правил. Во многих видах бизнеса болезненной проблемой считается потеря постоянных клиентов. В разных сферах (таких, как сотовая телефонная связь, фармацевтический бизнес или деятельность, связанная с кредитными карточками) ее обозначают различными терминами – "переменой моды", "истощением спроса" или "покупательской изменой", – но суть при этом одна. Классификация помогает выявить характеристики "неустойчивых" покупателей и создает модель, способную предсказать, кто именно склонен уйти к другому поставщику. Используя ее, можно определить самые эффективные виды скидок и других выгодных предложений, которые будут наиболее действенны для тех или иных типов покупателей. Благодаря этому удается удержать клиентов, потратив ровно столько денег, сколько необходимо, и не более.

Однажды определенный эффективный классификатор используется для классификации новых записей в базе данных в уже существующие классы, и в этом случае он приобретает характер прогноза. Например, классификатор, который умеет идентифицировать риск выдачи займа, может быть использован для целей принятия решения, велик ли риск предоставления займа определенному клиенту. То есть классификатор используется для прогнозирования возможности возврата займа.

Классическим примером применения классификации на практике является решение проблемы о возможной некредитоспособности клиентов банка. Этот вопрос, тревожащий любого сотрудника кредитного отдела банка, можно, конечно, разрешить интуитивно. Если образ клиента в сознании банковского служащего соответствует его представлению о кредитоспособном клиенте, то кредит выдавать можно, иначе – отказать. По схожей схеме работают установленные в тысячах американских банках системы добычи данных. Лишенные субъективной предвзятости, они опираются в своей работе только на историческую базу данных банка, где записывается детальная информация о каждом клиенте и, в конечном итоге, факт его кредитоспособности (вернул клиент ранее выданный кредит или нет). Клиенты банка в этих системах интерпретируются как векторы в пространстве 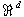, атрибутам которых соответствуют различные данные о клиентах (возраст, годовой доход, профессия и т. д.). Факт возврата (невозврата) кредита играет роль функции
y_i = {+1, -1}. Часть упомянутой исторической базы можно рассматривать как тренировочный набор данных, а другую часть – как обучающий набор. При таком подходе задача определения риска, связанного с клиентами, сводится к задаче построения классификатора. Решить ее можно с помощью нескольких методик. Также очевидно, что она имеет решение, поскольку интуитивно понятно, какого рода закономерности в данных обуславливают риск, связанный с клиентом. Высокий доход и хорошая профессия, безусловно, хороший аргумент в пользу благонадежности клиента.

В качестве методов решения задачи классификации могут использоваться алгоритмы типа Lazy-Learning [Wettschereck; Wang 99], в том числе известные алгоритмы ближайшего соседа и k-ближайших соседей [Aha 93, Aha 95], байесовские сети [Brand 98/2, Heckerman 95, Heckerman 97], деревья решений[Brand 98/1, Breiman 84, Quinlan 87, Quinlan 93, Гупал 93, Цветков 93], индукция символьных правил [Fuernkranz 96, Parsaye 97], нейронные сети [Уоссермен 92].

Регрессионный анализ используется в том случае, если отношения между переменными могут быть выражены количественно в виде некоторой комбинации этих переменных. Полученная комбинация далее используется для предсказания значения, которое может принимать целевая (зависимая) переменная, вычисляемая на заданном наборе значений входных (независимых) переменных. В простейшем случае для этого используются стандартные статистические методы, такие как линейная регрессия. К сожалению, большинство реальных моделей не укладываются в рамки линейной регрессии. Например, размеры продаж или фондовые цены очень сложны для предсказания, потому что могут зависеть от комплекса взаимоотношений множества переменных. Таким образом, необходимы комплексные методы для предсказания будущих значений.

Основные проблемы, с которыми сталкиваются при решении задач классификации и регрессии – это неудовлетворительное качество исходных данных, в которых встречается как шум, так и пропущенные значения, различные типы атрибутов – числовые и категорические, разная значимость атрибутов, а также, так называемые, проблемы "overfitting" и "underfitting". Суть первой из них, заключается в том, что классификационная функция при построении "чересчур хорошо" адаптируется к данным. И встречающийся в данных шум, и аномальные значения эта функция пытается интерпретировать как часть внутренней структуры данных. Очевидно, что такой классификатор будет некорректно работать в дальнейшем с другими данными, где характер шума будет несколько иной. Термином "underfitting" обозначают ситуацию, когда слишком велико количество ошибок при проверке классификатора на обучающем множестве. Это означает, что особых закономерности в данных не было обнаружено и, либо их нет вообще, либо необходимо выбрать иной метод их обнаружения.

Кластеризация логически продолжает идею классификации на более сложный случай, когда сами классы не предопределены. Результатом использования метода, выполняющего кластеризацию, как раз является определение (посредством свободного поиска) присущего исследуемым данным разбиения на группы.

Так можно выделить родственные группы клиентов или покупателей с тем, чтобы вести в их отношении дифференцированную политику. Например, "группы риска" – категории клиентов, готовых уйти к другому поставщику – средствами кластеризации могут быть определены до начала процесса ухода, что позволит производить профилактику проблемы, а не экстренное исправление положения. В большинстве случаев кластеризация очень субъективна: любой вариант разбиения на кластеры напрямую зависит от выбранной меры расстояния между объектами.

Для научных исследований изучение результатов кластеризации, а именно, выяснение причин, по которым объекты объединяются в группы, способно открыть новые перспективные направления. Традиционным примером, который обычно приводят для этого случая, является периодическая таблица элементов. В 1869 году Дмитрий Менделеев разделил 60 известных в то время элементов, на кластеры или периоды. Элементы, попадавшие в одну группу, обладали схожими характеристиками. Изучение причин, по которым элементы разбивались на явно выраженные кластеры, в значительной степени, определило приоритеты научных изысканий на годы вперед. Но лишь спустя пятьдесят лет квантовая физика дала убедительные объяснения периодической системы.

Кластеризация в чем-то аналогична классификации, но отличается от нее тем, что для проведения анализа не требуется иметь выделенную целевую переменную. Ее удобно использовать на начальных этапах исследования, когда о данных мало что известно. В большинстве других методов добычи данных исследование начинается, когда данные уже предварительно как-то расклассифицированы, хотя бы на обучающее множество данных и данные, по которым проверяется найденная модель или для которых надо предсказать целевую переменную. Для этапа кластеризации характерно отсутствие каких-либо различий, как между переменными, так и между записями. Напротив, ищутся группы наиболее близких, похожих записей.

Техника кластеризации применяется в самых разнообразных областях. Хартиган [Hartigan 1975] дал обзор многих опубликованных исследований, содержащих результаты, полученные методами кластерного анализа. Например, в области медицины кластеризация заболеваний, лечения заболеваний или симптомов заболеваний приводит к широко используемым таксономиям. В области психиатрии правильная диагностика кластеров симптомов, таких как паранойя, шизофрения и т. д., является решающей для успешной терапии. В археологии с помощью кластерного анализа исследователи пытаются установить таксономии каменных орудий, похоронных объектов и т.д. Известны широкие применения кластерного анализа в маркетинговых исследованиях. В общем, всякий раз, когда необходимо классифицировать "горы" информации к пригодным для дальнейшей обработки группам, кластерный анализ оказывается весьма полезным и эффективным.

Существует целый ряд алгоритмов кластеризации, позволяющих обнаруживать кластеры данных с любой степенью точности. Наиболее распространенные алгоритмы – это иерархическая кластеризация [Johnson 67, Gruvaeus 72] и метод k-средних [Hartigan 75, Hartigan 78]. В качестве примера других используемых методов можно привести обучение "без учителя" особого вида нейронных сетей – сетей Кохонена [Уоссермен 92], а также индукцию правил [Fuernkranz 96].

Выявление ассоциаций (другие названия: поиск ассоциативных правил, анализ рыночных корзин). Ассоциация имеет место в том случае, если несколько событий связаны друг с другом. Например, исследование "покупательской корзины", проведенное в супермаркете, может показать, что 65 % купивших кукурузные чипсы берут также и "кока-колу", а при наличии скидки за такой комплект "колу" приобретают в 85 % случаев. Располагая сведениями о подобной ассоциации, менеджерам легко оценить, насколько действенна предоставляемая скидка.

Кроме обширных практических приложений в области маркетинга, эта задача представляется важной и в ряде других приложений, связанных с объединением данных из различных источников. В частности, результаты анализа ассоциаций позволяют получать паттерны типа ассоциативных правил, которые далее могут использоваться для формирования продукционных баз знаний в системах поддержки принятия решений, обнаружения причин отказов аппаратуры, причин негативного или, наоборот, позитивного развития событий, ситуаций и т.п. Например, анализ ассоциаций, зависящих от времени, в последовательности событий входящего трафика компьютерной сети является основным источником информации для различения нормальной и аномальной деятельности пользователей.

Прогнозирование временных последовательностей (секвенциальный анализ) есть установление закономерностей между связанными во времени событиями. Метод позволяет на основе анализа поведения временных рядов оценить будущие значения прогнозируемых переменных. Конечно, эти модели должны включать в себя особые свойства времени: иерархию периодов (декада-месяц-год или месяц-квартал-год), особые отрезки времени (пяти-, шести- или семидневная рабочая неделя, тринадцатый месяц), сезонность, праздники и др.

Анализ рыночных корзин (Basket Analysis) и секвенциальный анализ являются в настоящий момент одними из самых популярных приложений добычи данных.

Агрегированием (обобщением) называют задачу поиска компактного описания подмножества данных. Примерами могут служить задача отыскания вектора средних значений и матрицы отклонений для набора данных, поиск функциональных зависимостей между переменными или ассоциативных правил и другие задачи. Поиск агрегированных описаний интерпретируется часто как поиск другого, в каком-то смысле лучшего, пространства представления данных. Типичным примером такого преобразования пространства представления данных является замена описания данных в терминах первичных атрибутов описанием их в терминах так называемых "аргументов" в пользу того или иного решения [Aha 95/1, Bundy 97], истинностные значения которых на конкретных входных данных затем используются для их классификации [Bull 97].

Обнаружение отклонений. Целью задачи является поиск наиболее значимых в заданном смысле изменений в данных по сравнению со средними, нормативными показателями.

3.3. Классификация систем добычи данных

Добыча данных является мультидисциплинарной областью, возникшей и развивающейся на базе достижений прикладной статистики, распознавания образов, методов искусственного интеллекта, теории баз данных и др. Отсюда обилие методов и алгоритмов, реализованных в различных действующих системах добычи данных. Многие из таких систем интегрируют в себе сразу несколько подходов. Тем не менее, как правило, в каждой системе имеется какой-то ключевой компонент, на который делается главная ставка. Ниже приводится классификация указанных ключевых компонентов на основе работ [Киселев 97, Дюк 01]:

• статистические методы;
• нейронные сети;
• деревья решений;
• системы рассуждения на основе аналогичных случаев;
• нечеткая логика;
• генетические алгоритмы;
• эволюционное программирование;
• алгоритмы ограниченного перебора;
• комбинированные методы.

Несмотря на то, что последние версии почти всех известных статистических пакетов включают наряду с традиционными статистическими методами также элементы добычи данных, основное внимание в них уделяется все же классическим методикам: корреляционному, регрессионному, факторному анализу и другим. Детальный обзор пакетов для статистического анализа приведен в [HTTP/1] Недостатком систем этого класса считается требование к специальной подготовке пользователя. Еще более серьезным принципиальным недостатком статистических пакетов, ограничивающим их применение в добыче данных, является то, что большинство методов, входящих в состав пакетов, опираются на статистическую парадигму, в которой главными фигурантами служат усредненные характеристики выборки. А они при исследовании реальных сложных жизненных феноменов часто являются фиктивными величинами.

Нейронные сети относятся к классу нелинейных адаптивных систем с архитектурой, условно имитирующей нервную ткань из нейронов. Математическая модель нейрона представляет собой некоторый универсальный нелинейный элемент с возможностью широкого изменения и настройки его характеристик. В одной из наиболее распространенных архитектур, многослойном перцептроне с обратным распространением ошибки, эмулируется работа нейронов в составе иерархической сети, где каждый нейрон более высокого уровня соединен своими входами с выходами нейронов нижележащего слоя. На нейроны самого нижнего слоя подаются значения входных параметров, на основе которых нужно принимать какие-то решения, прогнозировать развитие ситуации и т. д. Эти значения рассматриваются как сигналы, передающиеся в вышележащий слой, ослабляясь или усиливаясь в зависимости от числовых значений (весов), приписываемых межнейронным связям. В результате на выходе нейрона самого верхнего слоя вырабатывается некоторое значение, которое рассматривается как ответ, реакция всей сети на введенные значения входных параметров. Для того чтобы сеть можно было применять в дальнейшем, ее прежде надо "натренировать" на полученных ранее данных, для которых известны и значения входных параметров, и правильные ответы на них. Эта тренировка состоит в подборе весов межнейронных связей, обеспечивающих наибольшую близость ответов сети к известным правильным ответам.

Основным недостатком нейросетевой парадигмы является необходимость иметь очень большой объем обучающей выборки. Другой существенный недостаток заключается в том, что даже натренированная нейронная сеть представляет собой черный ящик. Знания, зафиксированные как веса нескольких сотен межнейронных связей, совершенно не поддаются анализу и интерпретации человеком, а известные попытки дать интерпретацию структуре настроенной нейросети выглядят неубедительными.

Деревья решений являются одним из наиболее популярных подходов к решению задач добычи данных. Они создают иерархическую структуру классифицирующих правил типа "если...то...", имеющую вид дерева. Для того чтобы решить, к какому классу отнести некоторый объект или ситуацию, требуется ответить на вопросы, стоящие в узлах этого дерева, начиная с его корня. Вопросы имеют вид "значение параметра A больше x?". Если ответ положительный, осуществляется переход к правому узлу следующего уровня, если отрицательный – то к левому узлу; затем снова следует вопрос, связанный с соответствующим узлом. В результате мы добираемся до одного из возможных вариантов решения.

Популярность деревьев решений связана с наглядностью и понятностью. Но для них очень остро стоит проблема значимости. Дело в том, что отдельным узлам на каждом новом построенном уровне дерева соответствует все меньшее и меньшее число записей данных – дерево дробит данные на большое количество частных случаев. Чем их больше, чем меньше обучающих примеров попадает в каждый такой частный случай, тем менее уверенной будет их классификация. Если построенное дерево слишком "кустистое" – состоит из неоправданно большого числа мелких веточек – оно не будет давать статистически обоснованных ответов. Как показывает практика, в большинстве систем, использующих деревья решений, эта проблема не находит удовлетворительного решения. Кроме того, общеизвестно, и это легко показать, что деревья решений дают полезные результаты только в случае независимых признаков. В противном случае они лишь создают иллюзию логического вывода.

Деревья решений принципиально не способны находить "лучшие" правила в данных. Они реализуют наивный принцип последовательного просмотра признаков и "цепляют" фактически осколки настоящих закономерностей, создавая лишь иллюзию логического вывода. Вместе с тем, большинство систем используют именно этот метод.

Нечеткая логика применяется для таких наборов данных, где причисление данных к какой-либо группе является вероятностью, находящейся в интервале от 0 до 1, но не принимающей крайние значения. Четкая логика манипулирует результатами, которые могут быть либо истиной, либо ложью. Нечеткая логика применяется в тех случаях, когда необходимо манипулировать степенью "может быть" в дополнении к "да" и "нет".

Добыча данных – далеко не основная область применения генетических алгоритмов, которые, скорее, нужно рассматривать в качестве мощного средства решения разнообразных комбинаторных задач и задач оптимизации. Тем не менее, генетические алгоритмы вошли сейчас в стандартный инструментарий методов добычи данных. Этот метод назван так потому, что в какой-то степени имитирует процесс естественного отбора в природе.

Предположим, требуется найти решение задачи, наиболее оптимальное с точки зрения некоторого критерия. Пусть каждое решение полностью описывается некоторым набором чисел или величин нечисловой природы. Если необходимо выбрать совокупность фиксированного числа параметров рынка, наиболее выразительным образом влияющих на его динамику, это будет набор имен этих параметров. О нем можно говорить как о совокупности хромосом, определяющих качества индивида – конкретного решения поставленной задачи. Значения параметров, определяющих решение, будут в этом случае называться генами. Поиск оптимального решения при этом похож на эволюцию популяции индивидов, представленных их наборами хромосом. В этой эволюции действуют три механизма: во-первых, отбор сильнейших, то есть тех наборов хромосом, которым соответствуют наиболее оптимальные решения; во-вторых, скрещивание – производство новых индивидов при помощи смешивания хромосомных наборов отобранных индивидов; и, в-третьих, мутации – случайные изменения генов у некоторых индивидов популяции. В результате смены поколений вырабатывается такое решение поставленной задачи, которое не может быть далее улучшено.

Генетические алгоритмы удобны тем, что их легко распараллеливать. Например, можно разбить поколение на несколько групп и работать с каждой из них независимо, обмениваясь, время от времени несколькими хромосомами. Существуют также и другие методы распараллеливания генетических алгоритмов.

Генетические алгоритмы имеют ряд недостатков. Критерий отбора хромосом и используемые процедуры являются эвристическими и далеко не гарантируют нахождения "лучшего" решения. Как и в реальной жизни, эволюцию может "заклинить" на какой-либо непродуктивной ветви. И, наоборот, можно привести примеры, как два неперспективных родителя, которые будут исключены из эволюции генетическим алгоритмом, оказываются способными произвести высокоэффективного потомка. Это особенно становится заметно при решении высокоразмерных задач со сложными внутренними связями.

Сама постановка задачи в терминах генетических алгоритмов не дает возможности проанализировать статистическую значимость получаемого с их помощью решения. Кроме того, эффективно сформулировать задачу, определить критерий отбора хромосом под силу только специалисту. В силу этих факторов сегодня генетические алгоритмы надо рассматривать скорее как инструмент научного исследования, чем как средство анализа данных для практического применения в бизнесе и финансах.

Эволюционное программирование – сегодня самая молодая и наиболее перспективная ветвь добычи данных. Суть метода заключается в том, что гипотезы о виде зависимости целевой переменной от других переменных формулируются системой в виде программ на некотором внутреннем языке программирования. Если это универсальный язык, то теоретически на нем можно выразить зависимость любого вида. Процесс построения этих программ строится подобно эволюции в мире программ (этим метод похож на генетические алгоритмы). Когда система находит программу, достаточно точно выражающую искомую зависимость, она начинает вносить в нее небольшие модификации и отбирает среди построенных таким образом дочерних программ те, которые повышают точность. Таким образом, система "выращивает" несколько генетических линий программ, которые конкурируют между собой в точности выражения искомой зависимости. Специальный транслирующий модуль переводит найденные зависимости с внутреннего языка системы на понятный пользователю язык (математические формулы, таблицы и пр.), делая их легкодоступными. Для того чтобы сделать полученные результаты еще понятнее для пользователя-нематематика, имеется богатый арсенал разнообразных средств визуализации обнаруживаемых зависимостей.

Поиск зависимости целевых переменных от остальных ведется в форме функций какого-то определенного вида. Например, в одном из наиболее удачных алгоритмов этого типа – методе группового учета аргументов (МГУА) зависимость ищут в форме полиномов. Причем сложные полиномы заменяются несколькими более простыми, учитывающими только некоторые признаки (групп аргументов). Обычно для этого используются попарные объединения признаков.

Алгоритмы ограниченного перебора были предложены в середине 60-х годов М. М. Бонгардом [Айвазян 89] для поиска логических закономерностей в данных. С тех пор они продемонстрировали свою эффективность при решении множества задач из самых различных областей.

Эти алгоритмы вычисляют частоты комбинаций простых логических событий в подгруппах данных. Примеры простых логических событий: X = a; X < a; X > a; a < X < b и др., где X — какой либо параметр, “a” и “b” — константы. Ограничением служит длина комбинации простых логических событий (у М. Бонгарда она была равна 3). На основании анализа вычисленных частот делается заключение о полезности той или иной комбинации для установления ассоциации в данных, для классификации, прогнозирования и пр.

Наиболее ярким современным представителем этого подхода является система WizWhy предприятия WizSoft [HTTP/2]. Хотя автор системы Абрахам Мейдан не раскрывает специфику алгоритма, положенного в основу работы WizWhy, по результатам тщательного тестирования системы были сделаны выводы о наличии здесь ограниченного перебора (изучались результаты, зависимости времени их получения от числа анализируемых параметров и др.).

Автор WizWhy утверждает, что его система обнаруживает все логические правила вида "если…то…" для поступающих данных. На самом деле это, конечно, не так. Во-первых, максимальная длина комбинации в правиле "если…то…" в системе WizWhy равна 6, и, во-вторых, с самого начала работы алгоритма производится эвристический поиск простых логических событий, на которых потом строится весь дальнейший анализ. Поняв эти особенности WizWhy, нетрудно было предложить простейшую тестовую задачу, которую система не смогла вообще решить. Другой момент — система выдает решение за приемлемое время только для сравнительно небольшой размерности данных (не более 20).

Тем не менее, система WizWhy является на сегодняшний день одним из лидеров на рынке продуктов добычи данных, что совсем не лишено оснований. Система постоянно демонстрирует более высокие показатели при решении практических задач, чем все остальные алгоритмы.

Комбинированные методы. Часто производители сочетают указанные подходы. Объединение в себе средств нейронных сетей и технологии деревьев решений должно способствовать построению более точной модели и повышению ее быстродействия. Программы визуализации данных в каком-то смысле не являются средством анализа информации, поскольку они только представляют ее пользователю. Тем не менее, визуальное представление, скажем, сразу четырех переменных достаточно выразительно обобщает очень большие объемы данных.

Для того чтобы найти новое знание на основе данных большого хранилища, недостаточно просто взять алгоритмы добычи данных, запустить их и ждать появления интересных результатов. Нахождение нового знания – это процесс, который включает в себя несколько шагов, каждый из которых необходим для уверенности в эффективном применении средств добычи данных.

Назад   Оглавление   Вперёд