Next: Задачи девятой олимпиады
Up: 7.5. Условия задач олимпиад
Previous: Задачи седьмой олимпиады
Contents: Содержание
8.1. На рисунке изображена эмблема олимпиады. Она
представляет собой замкнутую ленту, сложенную так, что образовавшиеся
просветы являются одинаковыми равносторонними треугольниками. Если в
некотором месте ленту разрезать перпендикулярно к ее краям и
развернуть, то получится прямоугольник. Найдите минимальное отношение
его сторон.
8.2. Сообщение, составленное из нулей и единиц, шифруется двумя
способами. При первом способе каждый нуль заменяется на
последовательность из  нулей и следующих за ними
нулей и следующих за ними  единиц, а
каждая единица заменяется на последовательность из
единиц, а
каждая единица заменяется на последовательность из  нулей. При
втором способе шифрования каждая единица заменяется на
последовательность из
нулей. При
втором способе шифрования каждая единица заменяется на
последовательность из  единиц и следующих за ними
единиц и следующих за ними  нулей, а
каждый нуль заменяется на последовательность из
нулей, а
каждый нуль заменяется на последовательность из  нулей. При каких
натуральных значениях
нулей. При каких
натуральных значениях  ,
,  , найдется хотя бы одно
сообщение, которое будет одинаково зашифровано обоими способами?
Укажите общий вид таких сообщений.
, найдется хотя бы одно
сообщение, которое будет одинаково зашифровано обоими способами?
Укажите общий вид таких сообщений.
8.3. Сообщение, подлежащее зашифрованию, представляет собой
цифровую последовательность, составленную из дат рождения 6 членов
оргкомитета олимпиады. Каждая дата представлена в виде
последовательности из 8 цифр, первые две из которых обозначают
день,следующие две - месяц, а остальные - год.
Например, дата рождения великого математика Л.Эйлера 4 апреля 1707
года представляется в виде последовательности 04041707. Для
зашифрования сообщения строится ключевая последовательность длины 48.
Для еепостроения все нечетные простые числа, меньшие 100,
выписываются через запятую в таком порядке, что модуль разности любых
двух соседних чисел есть та или иная степень числа 2. При этом каждое
простое число выписано ровно один раз, а числа 3, 5 и 7 записаны в виде
03, 05 и 07 соответственно. Удалив запятые
из записи этой последовательности, получим искомую ключевую
последовательность.
При зашифровании цифровой последовательности, представляющей
сообщение, ее цифры почленно складываются с соответствующими цифрами
ключевой последовательности, при этом каждая полученная сумма
заменяется ее остатком от деления на 10. В результате зашифрования
сообщения получена последовательность:
|
150220454213266744305682533362327363924975709849 |
Определите даты рождения членов оргкомитета олимпиады.
8.4. Квадрат размера
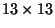 разбит на клетки размера
разбит на клетки размера  . В
начальный момент некоторые клетки окрашены в черный цвет, а
остальные - в белый. По клеткам квадрата прыгает Криптоша. В момент
попадания Криптоши в очередную клетку происходит изменение цвета на
противоположный у всех тех клеток, расстояния от центров которых до
центра клетки с Криптошей есть натуральные числа. После того как
Криптоша побывал в каждой клетке квадрата ровно 1999 раз, квадрат
оказался раскрашенным так, как показано на рисунке. Восстановите цвет
всех клеток квадрата в начальный момент.
. В
начальный момент некоторые клетки окрашены в черный цвет, а
остальные - в белый. По клеткам квадрата прыгает Криптоша. В момент
попадания Криптоши в очередную клетку происходит изменение цвета на
противоположный у всех тех клеток, расстояния от центров которых до
центра клетки с Криптошей есть натуральные числа. После того как
Криптоша побывал в каждой клетке квадрата ровно 1999 раз, квадрат
оказался раскрашенным так, как показано на рисунке. Восстановите цвет
всех клеток квадрата в начальный момент.
8.5. Для всех действительных чисел  ,
,  решите уравнение
решите уравнение
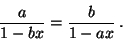
8.6. Разложите число  на простые множители.
на простые множители.
Next: Задачи девятой олимпиады
Up: 7.5. Условия задач олимпиад
Previous: Задачи седьмой олимпиады
Contents: Содержание