Next: 3.8. Вместо заключения Up: 3. Криптографические протоколы Previous: 3.6. Поиграем в ``кубики''. Contents: Содержание

3.7. За пределами стандартных предположений. Конфиденциальная передача сообщений

	``Ты умеешь считать? - спросила Белая Королева.- Сколько будет один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один? - Я не знаю, - ответила Алиса. - Я сбилась со счета. Она не умеет считать,- сказала Черная Королева.''

Л. Кэрролл. ``Алиса в зазеркалье''.

Криптографические протоколы в своем большинстве относятся к одной из двух категорий. В первую входят протоколы, обладающие теоретико-информационной или абсолютной стойкостью. Вторая категория - это те протоколы, стойкость которых основывается на вычислительной сложности каких-либо математических задач. Основывается в том смысле, что либо стойкость протокола доказана при некотором конкретном предположении, либо справедливость предположения необходима для стойкости, т.е. противник, научившийся решать соответствующую задачу эффективно, заведомо ``взламывает'' протокол.

В теоретической криптографии, как и во всякой научной дисциплине, представлено все многообразие направлений научного поиска. Одно из таких направлений - разработка криптографических схем, стойких при каких-либо нестандартных предположениях. Работ, посвященных этой тематике, немного, но они есть. И в этом заключительном разделе мы рассмотрим пример криптографического протокола, доказуемо стойкого при нестандартном предположении.

Задача конфиденциальной передачи сообщений состоит в следующем. Имеются два участника, Алиса и Боб, которые являются абонентами сети связи. Участники соединены проводами, по каждому из которых можно пересылать сообщения в обе стороны, независимо от того, что происходит с другими проводами. Никакой общей секретной информации у Алисы и Боба изначально нет. У Алисы имеется конфиденциальное сообщение , и задача состоит в том, чтобы его конфиденциальным же образом передать Бобу. Против участников действует активный противник, который может полностью контролировать не более проводов. Полный контроль означает, что противник перехватывает все сообщения, передаваемые по данному проводу, и может заменять их любыми другими сообщениями.

Если положить 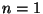и рассматривать пассивного противника, который только подслушивает, то получим классическую модель секретной связи, введенную еще Шенноном. Задача конфиденциальной передачи сообщений в этой модели всегда решалась с помощью криптосистем. Но выделение криптосистем в отдельную категорию - это, скорее, дань традиции. На самом деле требуется протокол конфиденциальной передачи сообщений, при построении которого используются такие криптографические примитивы, как алгоритмы шифрования и дешифрования, протокол распределения ключей и т.д. Например, в случае криптосистемы с открытым ключом примитивом может быть и протокол электронной подписи, если тот орган (центр доверия), которому поручено вести сертифицированный справочник, заверяет все открытые ключи, хранящиеся в этом справочнике, своей подписью.

В предположении 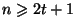задача конфиденциальной передачи сообщений может быть решена с помощью следующего простого протокола.

Прежде всего заметим, что при данном предположении Алиса и Боб имеют абсолютно надежный открытый канал связи. Если, например, Алисе необходимо послать сообщение Бобу, то она посылает по каждому из проводов, а Боб выбирает из всех полученных значений то, которое появилось по крайней мере 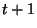раз.

Далее, пусть - большое простое число, . Алиса выбирает случайный полином 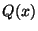степени над 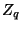. Пусть 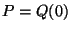. Идея состоит в том, чтобы передать Бобу в качестве одноразового ключа для шифра Вернама. При этом нужно обеспечить такую передачу, чтобы противник не мог узнать ничего о значении . Для этого Алиса использует пороговую схему разделения секрета, т.е. посылает значение по -му проводу. Пусть 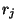, 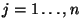- значение, которое Боб получил по -му проводу. Если все пар 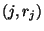интерполируются полиномом степени , то передача успешна и Боб может вычислить ключ . Далее Алиса и Боб общаются по описанному выше открытому каналу. Если Боб получил ключ , то он уведомляет об этом Алису специальным сообщением. Алиса вычисляет и посылает Бобу криптограмму 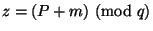. Боб дешифрует криптограмму и получает сообщение . Если пары 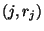не интерполируются полиномом степени , то Боб посылает все эти пары Алисе, которая обнаружит хотя бы для одного , что 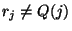. Ясно, что в этом случае провод контролируется противником. Алиса посылает Бобу список всех таких номеров , и соответствующие провода исключаются из работы. После этого Алиса и Боб повторяют весь протокол, используя оставшиеся провода. Ясно, что после не более повторений передача ключа будет успешной.

Данный протокол - простейший вариант протокола конфиденциальной передачи сообщений из работы Долева и др. [24]. В этой работе предложен значительно более эффективный протокол, который при том же предположении 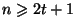является доказуемо стойким против более сильного противника.

Если противник пассивный, т.е. он лишь подслушивает не более проводов, то задача конфиденциальной передачи сообщений решается совсем просто. Мы предлагаем читателю в качестве несложного упражнения самостоятельно сконструировать соответствующий протокол при .

Протокол конфиденциальной передачи сообщений является доказуемо стойким в предположении, что противнику не хватает ресурсов, чтобы контролировать хотя бы половину проводов, которыми соединены Алиса и Боб. Этот результат наводит на следующие размышления. Так называемый здравый смысл подсказывает, что для построения системы секретной связи целесообразно создать закрытую сеть связи, т.е. такую, доступ к которой сильно ограничен. Но, по-видимому, действительно надежное решение следует искать в прямо противоположном направлении: объединить все сети связи в единую открытую сеть с очень большим количеством соединений между каждой парой абонентов. Конечно, это - всего лишь теоретические рассуждения, относящиеся к математической модели реальных систем. Но сколько раз еще результаты, полученные в математической криптографии, как и в любых других научных дисциплинах, заставят нас усомниться в очевидности тех решений, которые подсказываются здравым смыслом.

Next: 3.8. Вместо заключения Up: 3. Криптографические протоколы Previous: 3.6. Поиграем в ``кубики''. Contents: Содержание