Next: 2.3. Односторонние функции
Up: 2. Криптография и теория
Previous: 2.1. Введение
Contents: Содержание
Как правило, знакомство математиков-неспециалистов с
теорией
сложности вычислений ограничивается классами P и NP и знаменитой
гипотезой P NP.
NP.
Напомним вкратце необходимые
сведения из теории сложности вычислений. Пусть  -
множество всех конечных строк в двоичном
алфавите
-
множество всех конечных строк в двоичном
алфавите
 . Подмножества
. Подмножества
 в теории
сложности принято называть языками. Говорят, что
машина
Тьюринга
в теории
сложности принято называть языками. Говорят, что
машина
Тьюринга  работает за полиномиальное время (или просто,
что она полиномиальна), если существует полином
работает за полиномиальное время (или просто,
что она полиномиальна), если существует полином  такой,
что на любом входном слове длины
такой,
что на любом входном слове длины  машина
машина  останавливается
после выполнения не более, чем
останавливается
после выполнения не более, чем 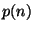 операций. Машина
Тьюринга
операций. Машина
Тьюринга  распознает (другой термин - принимает) язык
распознает (другой термин - принимает) язык
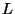 , если на всяком входном слове
, если на всяком входном слове 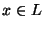 машина
машина  останавливается в принимающем состоянии, а на всяком слове
останавливается в принимающем состоянии, а на всяком слове
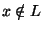 - в отвергающем. Класс P - это класс всех
языков, распознаваемых машинами Тьюринга, работающими за
полиномиальное время. Функция
- в отвергающем. Класс P - это класс всех
языков, распознаваемых машинами Тьюринга, работающими за
полиномиальное время. Функция
 вычислима за полиномиальное время, если существует
полиномиальная машина Тьюринга
такая, что если на вход ей подано слово
вычислима за полиномиальное время, если существует
полиномиальная машина Тьюринга
такая, что если на вход ей подано слово  ,
то в момент останова на ленте
будет записано значение
,
то в момент останова на ленте
будет записано значение  .
Язык
.
Язык 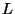 принадлежит классу NP, если существуют
предикат
принадлежит классу NP, если существуют
предикат
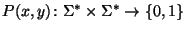 ,
вычислимый за полиномиальное время, и полином
,
вычислимый за полиномиальное время, и полином
 такие, что
такие, что
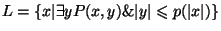 . Таким образом, язык
. Таким образом, язык 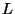 принадлежит NP, если
для всякого слова из
принадлежит NP, если
для всякого слова из 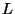 длины
длины  можно угадать некоторую
строку полиномиальной от
можно угадать некоторую
строку полиномиальной от  длины и затем с помощью
предиката
длины и затем с помощью
предиката  убедиться в правильности догадки. Ясно, что
убедиться в правильности догадки. Ясно, что
 . Является ли это включение строгим - одна
из самых известных нерешенных задач математики. Большинство
специалистов считают, что оно строгое (так называемая
гипотеза P
. Является ли это включение строгим - одна
из самых известных нерешенных задач математики. Большинство
специалистов считают, что оно строгое (так называемая
гипотеза P NP). В классе NP выделен подкласс
максимально сложных языков, называемых NP-полными: любой
NP-полный язык распознаваем за полиномиальное время тогда и
только тогда, когда P=NP.
NP). В классе NP выделен подкласс
максимально сложных языков, называемых NP-полными: любой
NP-полный язык распознаваем за полиномиальное время тогда и
только тогда, когда P=NP.
Для дальнейшего нам потребуется еще понятие вероятностной
машины Тьюринга. В
обычных машинах Тьюринга (их
называют детерминированными, чтобы
отличить от вероятностных) новое состояние, в которое машина
переходит на очередном шаге, полностью определяется текущим
состоянием и тем символом, который обозревает головка на
ленте. В вероятностных
машинах новое состояние может
зависеть еще и от случайной величины, которая принимает
значения 0 и 1 с вероятностью  каждое. Альтернативно,
можно считать, что вероятностная машина Тьюринга имеет
дополнительную случайную ленту, на которой записана
бесконечная двоичная случайная строка. Случайная лента
может читаться только в одном направлении и переход в новое
состояние может зависеть от символа, обозреваемого на этой
ленте.
каждое. Альтернативно,
можно считать, что вероятностная машина Тьюринга имеет
дополнительную случайную ленту, на которой записана
бесконечная двоичная случайная строка. Случайная лента
может читаться только в одном направлении и переход в новое
состояние может зависеть от символа, обозреваемого на этой
ленте.
Рассмотрим теперь следующий естественный вопрос: не является ли
гипотеза P NP необходимым и достаточным условием для существования
стойких криптографических схем?
NP необходимым и достаточным условием для существования
стойких криптографических схем?
Необходимость, и в самом деле, во многих случаях почти
очевидна.
Вернемся к примеру 1.
Определим следующий язык
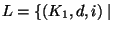 существует сообщение
существует сообщение  такое, что
такое, что
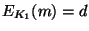 и его
и его  -ый бит равен 1
-ый бит равен 1 .
.
Ясно, что
 : вместо описанного во введении полного перебора
можно просто угадать открытый
текст
: вместо описанного во введении полного перебора
можно просто угадать открытый
текст  и проверить за полиномиальное время, что
и проверить за полиномиальное время, что
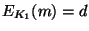 и
и  -ый бит
-ый бит  равен 1. Если да, то
входное слово
равен 1. Если да, то
входное слово 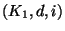 принимается, в противном случае - отвергается.
принимается, в противном случае - отвергается.
В предположении P=NP существует детерминированный
полиномиальный алгоритм, распознающий язык 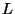 . Зная
. Зная  и
и  , с помощью этого алгоритма можно последовательно, по
биту, вычислить открытый текст
, с помощью этого алгоритма можно последовательно, по
биту, вычислить открытый текст  . Тем самым криптосистема нестойкая.
. Тем самым криптосистема нестойкая.
Тот же подход: угадать секретный ключ и проверить (за
полиномиальное время) правильность догадки, применим в
принципе и к другим криптографическим схемам. Однако, в
некоторых случаях возникают технические трудности,
связанные с тем, что по информации, которая имеется у
противника, искомая величина (открытый текст, секретный
ключ и т.п.) восстанавливается неоднозначно.
Что же касается вопроса о достаточности предположения
P NP, то здесь напрашивается следующий подход: выбрать
какую-либо NP-полную задачу и построить на ее основе
криптографическую схему, задача взлома которой (т.е. задача, стоящая перед противником) была бы NP-полной. Такие
попытки предпринимались в начале 80-х годов, в особенности в
отношении криптосистем с открытым ключом, но к успеху не
привели. Результатом всех этих попыток стало осознание
следующего факта: даже если P
NP, то здесь напрашивается следующий подход: выбрать
какую-либо NP-полную задачу и построить на ее основе
криптографическую схему, задача взлома которой (т.е. задача, стоящая перед противником) была бы NP-полной. Такие
попытки предпринимались в начале 80-х годов, в особенности в
отношении криптосистем с открытым ключом, но к успеху не
привели. Результатом всех этих попыток стало осознание
следующего факта: даже если P NP, то любая NP-полная
задача может оказаться трудной лишь на некоторой
бесконечной последовательности входных слов. Иными словами,
в определение класса NP заложена мера сложности ``в худшем
случае''. Для стойкости же криптографической схемы
необходимо, чтобы задача противника была сложной ``почти
всюду''.
Таким образом, стало ясно, что для криптографической
стойкости необходимо существенно более сильное
предположение, чем P
NP, то любая NP-полная
задача может оказаться трудной лишь на некоторой
бесконечной последовательности входных слов. Иными словами,
в определение класса NP заложена мера сложности ``в худшем
случае''. Для стойкости же криптографической схемы
необходимо, чтобы задача противника была сложной ``почти
всюду''.
Таким образом, стало ясно, что для криптографической
стойкости необходимо существенно более сильное
предположение, чем P NP. А именно, предположение о
существовании односторонних функций.
NP. А именно, предположение о
существовании односторонних функций.
Next: 2.3. Односторонние функции
Up: 2. Криптография и теория
Previous: 2.1. Введение
Contents: Содержание