Next: 5. Оценка секретных систем
Up: Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ
Previous: 3. Способы изображения систем
Contents: Содержание
В данном разделе рассматриваются несколько примеров шифров. В дальнейшем
в целях иллюстрации будем часто ссылаться на эти примеры.
1. Шифр простой подстановки.
В таком шифре производится замена каждой
буквы сообщения на некоторый
определенный символ (обычно также на букву).
Таким образом, сообщение
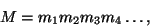
где
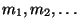
-- последовательные буквы, переходит в

причем функция

имеет обратную функцию. Ключ является
просто перестановкой алфавита (если буквы заменяются на
буквы), например,

Первая
буква --

заменяет букву

,
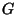
заменяет
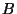
и т.д.
2. Транспозиция с фиксированным периодом  .
.
В этом случае сообщение делится
на группы символов длины  и
к каждой группе применяется одна и та же перестановка. Эта
перестановка является ключом; она может быть задана некоторой
перестановкой первых
и
к каждой группе применяется одна и та же перестановка. Эта
перестановка является ключом; она может быть задана некоторой
перестановкой первых  целых чисел.
целых чисел.
Таким образом, для  в
качестве перестановки можно взять 23154. Это будет означать, что
в
качестве перестановки можно взять 23154. Это будет означать, что
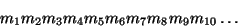
переходит в

Последовательное применение двух или более транспозиций будет
называться составной транспозицией. Если периоды этих
транспозиций

, ...,
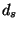
, то, очевидно, в результате получится
транспозиция периода

, где

-- наименьшее общее кратное
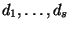
.
3. Шифр Виженера и его варианты.
В шифре Виженера ключ задается набором
из  букв. Такие
наборы подписываются с повторением под сообщением и полученные
две последовательности складываются по модулю 26 (каждая буква
рассматриваемого алфавита нумеруется от
букв. Такие
наборы подписываются с повторением под сообщением и полученные
две последовательности складываются по модулю 26 (каждая буква
рассматриваемого алфавита нумеруется от  до
до 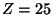 ).
).
Таким образом,
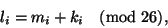
где

-- буква ключа, полученная сокращением числа

по модулю

. Например, с помощью ключа

получаем
| Сообщение |
 |
 |
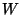 |
 |
 |
 |
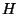 |
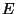 |
| Повторяемый ключ |
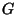 |
 |
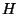 |
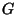 |
 |
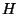 |
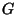 |
 |
| Криптограмма |
 |
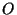 |
 |
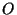 |
 |
 |
 |
 |
Шифр Виженера с периодом 1 называется
шифром Цезаря. Он
представляет собой простую подстановку, в которой каждая буква
сообщения  сдвигается вперед на фиксированное число мест по
алфавиту. Это число и является ключом; оно может быть любым от 0
до 25. Так называемый шифр Бофора (Beaufort) и видоизмененный
шифр Бофора подобны шифру Виженера. В них сообщения
зашифровываются с помощью равенств
сдвигается вперед на фиксированное число мест по
алфавиту. Это число и является ключом; оно может быть любым от 0
до 25. Так называемый шифр Бофора (Beaufort) и видоизмененный
шифр Бофора подобны шифру Виженера. В них сообщения
зашифровываются с помощью равенств

соответственно. Шифр Бофора с периодом 1 называется обратным
шифром Цезаря.
Повторное применение двух или более шифров Виженера будет
называться составным шифром Виженера. Он имеет уравнение

где
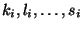
вообще говоря, имеют различные периоды.
Период их суммы

,
как и в составной транспозиции, будет наименьшим общим кратным
отдельных периодов.
Если используется шифр Виженера с неограниченным
неповторяющимся ключом, то мы имеем шифр Вернама,
в котором

и

выбираются случайно и независимо среди чисел 0, 1, ..., 25.
Если ключом служит текст, имеющий смысл,
то имеем шифр ``бегущего
ключа''.
4. Диграммная, триграммная и  -граммная подстановки.
-граммная подстановки.
Вместо подстановки одной буквы можно использовать подстановку
диграмм, триграмм и т.д. Для
диграммной подстановки в общем
виде требуется ключ, состоящий из перестановок 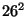 диграмм. Он
может быть представлен с помощью таблицы, в которой ряд
соответствует первой букве диграммы, а столбец -- второй букве,
причем клетки таблицы заполнены заменяющими символами (обычно
также диграммами).
диграмм. Он
может быть представлен с помощью таблицы, в которой ряд
соответствует первой букве диграммы, а столбец -- второй букве,
причем клетки таблицы заполнены заменяющими символами (обычно
также диграммами).
5. Шифр Виженера с перемешанным один раз алфавитом.
Такой шифр
представляет собой простую подстановку с
последующим применением шифра Виженера
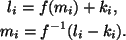
``Обратным''
к такому шифру является шифр Виженера с последующей
простой подстановкой
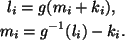
6. Матричная система
Имеется
один метод подстановки  -грамм, который заключается в
применении к последовательным
-грамм, который заключается в
применении к последовательным  -граммам некоторой матрицы,
имеющей обратную. Предполагается, что буквы занумерованы от 0
до 25 и рассматриваются как элементы некоторого алгебраического
кольца. Если к
-граммам некоторой матрицы,
имеющей обратную. Предполагается, что буквы занумерованы от 0
до 25 и рассматриваются как элементы некоторого алгебраического
кольца. Если к  -грамме сообщения применить матрицу
-грамме сообщения применить матрицу 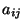 , то
получится
, то
получится  -грамма криптограммы
-грамма криптограммы

Матрица 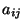 является ключом, и расшифровка выполняется с
помощью обратной матрицы. Обратная матрица будет
существовать тогда и только тогда, когда определитель
является ключом, и расшифровка выполняется с
помощью обратной матрицы. Обратная матрица будет
существовать тогда и только тогда, когда определитель 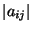 имеет обратный элемент в нашем кольце.
имеет обратный элемент в нашем кольце.
7. Шифр Плэйфер
Этот шифр является частным видом диграммной подстановки,
которая производится с помощью перемешанного алфавита из 25
букв, записанных в виде квадрата  . (Буква
. (Буква 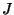 часто опускается
при криптографической работе, так как она редко встречается, и
в тех случаях, когда она встречается, ее можно заменить буквой
часто опускается
при криптографической работе, так как она редко встречается, и
в тех случаях, когда она встречается, ее можно заменить буквой
 ). Предположим, что ключевой квадрат записывается следующим
образом:
). Предположим, что ключевой квадрат записывается следующим
образом:
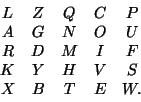
В этом случае диграмма

, например, заменяется на пару букв,
расположенных в противоположных углах прямоугольника,
определяемого буквами

и

, т.е. на

, причем
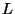
взята
первой, так как она выше

. Если буквы диграммы расположены
на одной горизонтали, то используются
стоящие справа от них буквы.
Таким образом,

заменяется на

,

заменяется на

. Если
буквы расположены на одной вертикали, то используются буквы, стоящие
под ними. Таким образом,
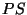
заменяется на

. Если обе буквы
диграммы совпадают, то можно использовать для их разделения нуль или же
одну из букв опустить и т.п.
8. Перемешивание алфавита с помощью многократной подстановки.
В этом шифре используются последовательно  простых
подстановок. Так, если
простых
подстановок. Так, если  , то
, то

заменяется на
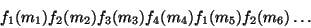
и т.д.
9. Шифр с автоключом.
Шифр типа Виженера, в котором или само сообщение или
результирующая криптограмма используются в качестве
``ключа'', называется шифром с автоключом. Шифрование начинается
с помощью ``первичного ключа'' (который является настоящим ключом
в нашем смысле) и продолжается с помощью сообщения или
криптограммы, смещенной на длину первичного ключа, как в
указанном ниже примере, где первичным ключом является набор букв
 . В качестве ``ключа'' используется сообщение:
. В качестве ``ключа'' используется сообщение:
| Сообщение |
 |
 |
 |
 |
 |
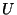 |
 |
 |
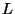 |
 |
 |
 |
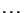 |
| Ключ |
 |
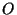 |
 |
 |
 |
 |
 |
 |
 |
 |
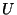 |
 |
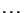 |
| Криптограмма |
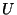 |
 |
 |
 |
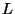 |
 |
 |
 |
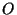 |
 |
 |
 |
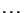 |
Если в качестве ``ключа'' использовать криптограмму, то
получится1)
| Сообщение |
 |
 |
 |
 |
 |
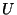 |
 |
 |
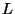 |
 |
 |
 |
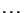 |
| Ключ |
 |
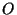 |
 |
 |
 |
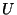 |
 |
 |
 |
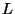 |
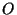 |
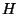 |
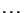 |
| Криптограмма |
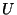 |
 |
 |
 |
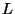 |
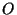 |
 |
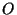 |
 |
 |
 |
 |
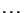 |
10. Дробные шифры.
В этих шифрах каждая буква сначала
зашифровывается в две
(или более) буквы или в два (или более) числа, затем полученные
символы каким-либо способом перемешиваются (например, с помощью
транспозиции), после чего их можно снова перевести в
первоначальный алфавит. Таким образом, используя в качестве
ключа перемешанный25-буквенный алфавит, можно перевести
буквы в двухзначные пятеричные числа с помощью таблицы:

Например, букве 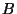 соответствует ``число'' 41. После того как
полученный ряд чисел подвергнут некоторой перестановке, его
можно снова разбить на пары чисел и перейти к буквам.
соответствует ``число'' 41. После того как
полученный ряд чисел подвергнут некоторой перестановке, его
можно снова разбить на пары чисел и перейти к буквам.
11. Коды.
В кодах слова (или иногда слоги) заменяются группами букв.
Иногда затем применяется шифр того или иного вида.
Next: 5. Оценка секретных систем
Up: Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ
Previous: 3. Способы изображения систем
Contents: Содержание