Обзор алгоритмов MOLAP. Quotient Cube

Данные Разработка Безопасность Инфраструктура Курсы и книги

2008 г.

Обзор алгоритмов MOLAP

Вперед: Библиография Выше: Семантические алгоритмы Назад: Condensed Cube Содержание

Подразделы

Quotient Cube

Разбиение на классы ячеек

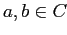
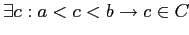
Идея этого алгоритма состоит в том, чтобы вместо хранения всех ячеек куба хранить только классы ячеек с одинаковым значением агрегирующей функции. Если же указать выпуклое разбиение (т.е. если две ячейки $a,b \in C$ и $\exists c: a<c<b \rightarrow c\in C$ ), достаточно будет хранить только верхние и нижние грани классов, т.к. все ячейки класса можно будет вывести из этих границ.

Однако разбиение только по значению агрегирующей функции разрушает семантику куба (и тем более не выпукло). Покажем это.

Например, рассмотрим еще раз таблицу Продажи из введения (Таблица 5.1). Получившиеся разбиение изображено на рис. 5.1.

**Таблица 5.1:** Копия таблицы 1.1
$\displaystyle \begin{tabular}{\vert c\vert c\vert c\vert c\vert} \hline Регион ... ...e R1 & Еда & Осень & 3\\ \hline R2 & книги & Осень & 6\\ \hline \end{tabular}$

Рис. 5.1: Разбиение только по значению агрегирующей функции

У нас получается следующая схема (рисунок 5.2).

**Рис. 5.2:** Классы при разбиении только по значению агрегирующей функции

Выбор агрегирующей функции в данном случае не важен, т.к. у нас есть возможность двигаться в обе стороны по отношениям roll-up/drill-down. Например, можно пойти вверх от ячейки (ALL, ALL, ALL) в С2 в ячейку (ALL, книги, ALL) в C5, а потом в (R2, книги, ALL) в С2. Тем самым, нарушается семантика отношений roll-up/drill-down.

Таким образом, мы показали, что разбиение только по значению агрегирующей функции не порождает связанной решетки классов эквивалентности. Необходимы какие-то ограничения.

В первых работах по данному алгоритму в качестве разбиения предлагалось так называемое связанное разбиение, однако оно верно только для монотонных функций (Sum (слагаемые одного знака), Count и пр). Впоследствии было предложено разбиение по покрытию. Поэтому здесь в примерах используется AVG — немонотонная функция.

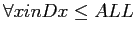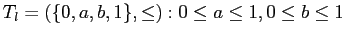Будем рассматривать кортежи куба как решетку (CL(r), Cube Lattice над отношением r) с введенным порядком, определенным иерархиями измерений (т.е. $\forall x in D x \le ALL$ ). Введем определение покрытия для решетки (см [1],[2]) $T_l=(\{0,a,b,1\},\le): 0\le a \le 1, 0\le b\le 1$ .

Определение 5.2 Будем говорить, что в частично упорядоченном множестве $(A,\le)$ элемент а покрывает элемент b, или b покрывается элементом a (обозначение: $a\succ b$ или $b\prec a$ ), если:

не существует , такого, что

Следующая лемма показывает, что отношение покрываемости будет определять частичный порядок на множестве.

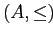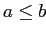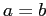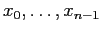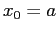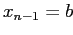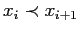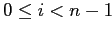Лемма 1 Если $(A,\le)$ — конечное частично упорядоченное множество, то $a\le b$ тогда и только тогда, когда , или когда существует конечная последовательность элементов $x_0, \ldots,x_{n-1}$ такая, что , $x_{n-1}=b$ и $x_i\prec x_{i+1}$ для $0\le i < n-1$ .

Отношение покрываемости в решетке

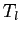
будет выглядеть следующим образом:

$\displaystyle \prec = \{(0,a),(0,b),(a,1),(b,1)\}$

На диаграмме частично упорядоченного множества 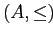$(A,\le)$ элементы изображаются в виде маленьких кружочков 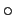$\circ$ ; кружки, соответствующие элементам x и у, соединяются прямой линией тогда и только тогда, когда один из них покрывает другой; если x покрывает y, то кружок, соответствующий элементу x, помещается выше кружка, соответствующего элементу y. Отметим, что в диаграмме пересечение двух линий не обозначает элемент. Диаграмма для решетки 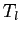изображена на рисунке 5.3.

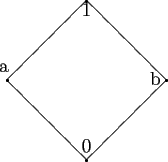
**Рис. 5.3:** Диаграмма решетки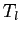
$\begin{figure} \begin{picture}(106,106) \put(5,55){\circle*{2}} \put(0,60){a}... ...105){\line(1,-1){50}} \put(105,55){\line(-1,-1){50}} \end{picture} \end{figure}$

Определение 5.3 Отношение покрытия для решетки куба

Кортеж $c \in CL(r)$ покрывает базовый (фактический) кортеж $t \in r$ , если $c\ge_g t$ .

Определение 5.4 Отношение эквивалентности по покрытию

Определим отношение эквивалентности 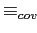$\equiv_{cov}$ как транзитивное и рефлексивное замыкание 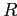, где:

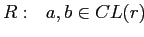
$R:~~a,b \in CL(r)$

$\displaystyle R(a,b) \Longleftrightarrow \exists T\in CL(r), \forall t \in T \l... ... t' \notin T: t'\in r\\ ,a\ge_g t' ~\mbox{или}~b\ge_g t'\\ \end{array}\right.$

Введенные определения и теоремы позволяют утверждать, что разбиение по покрытию формирует полную решетку куба, только ячейками этой решетки будут являться классы ячеек обычной решетки. Причем у каждого класса будет существовать верхняя и нижняя грань, решетка будет связанной и выпуклой. Значения всех дистрибутивных и алгебраических функций для всех ячеек подобного класса эквивалентности будет совпадать.

Рассмотрим тот же пример, только на этот раз разбиение будет вестись по покрытию (рис. 5.4).

Рис. 5.4: Разбиение по покрытию

Соответствующая решетка по классам показана на рис. 5.5.

Рис. 5.5: Классы разбиения по покрытию

Таким образом, для получившегося куба нам нужно хранить только две ячейки на класс, верхнюю и нижнюю грань. Остальные ячейки выводятся из верхней и нижней грани, т.к. классы разбиения по покрытиям''полны'' в смысле введенного частичного порядка.

Для Quotient Cube предложено две структуры хранения данных: QC - Tables [12] и QC-Trees [11].

QC-Table — простая таблица, в которой для каждого класса хранится верхняя и нижняя грань. Предложены алгоритмы создания QC-Table и вставки/удаления классов. Такие таблицы неэффективны по времени обработки запросов, т.к. каждый запрос требует просмотра почти всей таблицы.

QC-Trees

QC-Tree — дерево с разделением префиксов, где грани представляются строчками, а связи отражают необходимые отношения drill-down. Основной идеей QC-деревьев является то, что верхние грани классов куба хранят всю необходимую информацию для выполнения запросов. Т.е. при данном подходе не хранятся даже нижние грани классов. При такой структуре хранения данных запросы над Quotient-кубами выполняются эффективнее запросов над DWARF-кубами. Достигается это превосходство на основе аналогичного по смыслу устранения суффиксной и префиксной избыточностей. QC-деревья позволяют устранять суффиксную избыточность за счет того, что хранятся только классы, а не отдельные ячейки. Префиксная избыточность устраняется за счет свойств самой структуры QC-tree.

Определение 5.5 QC-Tree куба Q — это орграф 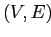, в котором:

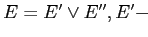$E = E' \vee E'', E' -$ ребра и 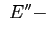связи, причем 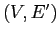— это дерево;
каждая вершина содержит метку, равную значению одного из измерений;
для каждой верхней грани 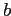существует и единственна вершина 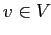$v \in V$ такая, что строчное представление 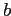совпадает с последовательностью меток вершин на пути от корня к 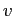в (V,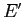 ); эта вершина хранит агрегирующее значение для .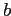
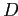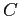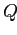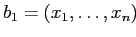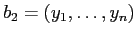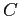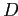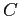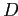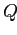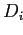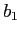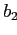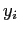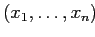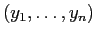предположим, что и — классы в , $b_1 = (x_1,\ldots,x_n)$ и $b_2 = (y_1,\ldots,y_n)$ — их верхние грани, и что — потомок (например, что напрямую специализирует (drills-down) ) в ; тогда для каждого измерения , на котором различаются и , существует либо ребро дерева, либо связь (маркированная ) из вершины $(x_1,\ldots,x_n)$ в вершину $(y_1,\ldots,y_n)$ .

Только последнее из условий требует каких-либо объяснений. Оно просто утверждает, что если С напрямую специализирует D в Q, то это возможно либо по ребру дерева, либо по связи из какого-либо префикса пути, представляющего верхнюю грань С, к вершине, которая приведет к верхней грани D.

**Таблица 5.2:** Классы и верхние грани Quotient Cube
Класс	Верхняя Грань
С1	(ALL,ALL,ALL)
С2	(R1,ALL,ALL)
С3	(ALL,книги,ALL)
С4	(ALL,ALL,осень)
С5	(R1,книги,весна)
С6	(R1,еда,осень)
С7	(R2,книги,осень)

Рис. 5.6: QC-Tree

Доказана теорема, о том, что QC-дерево для каждого Quotient куба уникально. Существуют алгоритмы создания/поддержки QC-деревьев. Выполнение запросов на QC-деревьях сильно отличается от аналогичных алгоритмов в других методах, т.к. необходимо ''выводить'' содержимое ячейки из верхней и нижней гранях класса. Аналогично, поддержка изменений информации требует пересмотра решетки классов, что, в общем случае, замедляет внесение изменений. В таблице 5.2 показаны классы и верхние грани Quotient-куба для примерных данных из таблицы 5.1, а на рис. 5.6 — соответствующее QC-Tree.

Выполнение различных типов запросов

Точечные запросы

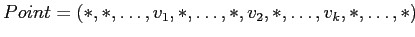
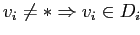
$Point = (*,*,\ldots,v_1,*,\ldots,*,v_2,*,\ldots,v_k,*,\ldots,*)$ , где если $v_i\ne *\Rightarrow v_i \in D_i$ , — точечный запрос. Требуется вернуть значение меры в точке, определенной

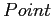
Алгоритм.

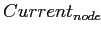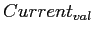$Current_{node}$ = корень; $Current_{val}$ =
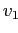
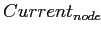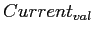На любом узле $Current_{node}$ искать дугу с меткой $Current_{val}$ ,
если существует:
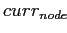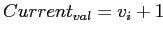
$curr_{node}$ = потомок по найденной дуге; $Current_{val} = v_i + 1$
иначе: проверить последнее измерение j, по которому у 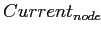$Current_{node}$ есть потомок.
Если 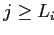$j\ge L_i$ , тогда 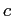в кубе не появится.
Иначе: 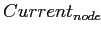$Current_{node}$ = потомок по измерению j, снова повторяем 2.

Примеры

(R2,*,осень) $\rightarrow$ начинаем с корня, находим вершину 7, в вершине 7 ищем ''осень'', берем потомка по измерению, продукты, попадаем в 9 — есть ответ.
(R2,*,весна) $\rightarrow$ все тоже самое, но в 9 мы будем пытаться найти ''весна'' $\rightarrow$ такой ячейки нет $\rightarrow$ (*,еда,*) $\rightarrow$ в 5, но там нет значения, ''проваливаемся'' в 6 — ответ

Интервальные запросы

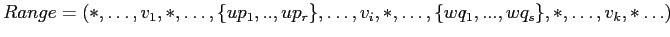
Запрос: $Range = (*,\ldots,v_1,*,\ldots, \{up_1,..,up_r\},\ldots,v_i,*,\ldots,\{wq_1,...,wq_s\},*,\ldots,v_k,*\ldots)$ . Можно превратить такой запрос в серию точечных запросов, но эффективней во время обработки каждого интервала исключать все недостижимые ячейки. Пример:

Порядок обработки запроса (*, книги, еда, весна) следующий:

корень $\rightarrow$ книги $\rightarrow$ весна — возвращается значение;

корень $\rightarrow$ еда — но не можем попасть в ''весну''.

Обратные запросы

Прямой оптимизации по выполнению обратных запросов метод не дает. Но возможно построение индексов B+ деревьев по мерам в QC-деревьях. Это поможет в выполнении обратных запросов, не накладывающих ограничений на измерения. В случае наличия ограничений в запросе можно оставить в QC-дереве только вершины, удовлетворяющие условию и их предков. Получится поддерево, на котором нужно выполнить интервальный запрос.

Intelligent Roll-Up Queries

Также необходимо отметить, что метод Quotient-кубов дает быстрый ответ на так называемые "умные" roll-up запросы (Intelligent Roll-Up Queries). Ответ на данные запросы дается во время построения Quotient-кубов, т.к. это и есть верхние и нижние границы кубов.

Вперед: Библиография Выше: Семантические алгоритмы Назад: Condensed Cube Содержание