2008 г.
Методы бикластеризации для анализа интернет-данных
Дмитрий Игнатов,
кафедра анализа данных и искусственного интеллекта ГУ-ВШЭ
Назад Содержание Вперёд
2.5.2. Алгоритм Apriori
Рассмотрим алгоритм Apriori, ставший первым эффективным алгоритмом поиска частых множеств признаков. Алгоритм Apriori предназначен для поиска всех частых множеств признаков. Он является поуровневым, использует стратегию поиска в ширину и осуществляет его снизу-вверх. В алгоритме используются две структуры данных: 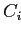 — для хранения множества кандидатов в частые множества признаков длины
— для хранения множества кандидатов в частые множества признаков длины 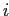 и
и 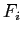 — для хранения частых множеств признаков длины
— для хранения частых множеств признаков длины 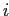 .
Каждая структура имеет два поля — itemset, сохраняющее множество признаков, и support, которое хранит величину поддержки этого множества признаков. Алгоритм представлен в виде псевдокода и состоит из двух частей: самого Apriori — алгоритм 2.5.1 и вспомогательной процедуры AprioriGen — алгоритм 2.5.2 .
.
Каждая структура имеет два поля — itemset, сохраняющее множество признаков, и support, которое хранит величину поддержки этого множества признаков. Алгоритм представлен в виде псевдокода и состоит из двух частей: самого Apriori — алгоритм 2.5.1 и вспомогательной процедуры AprioriGen — алгоритм 2.5.2 .
Процедура AprioriGen для 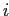 -элементных частых множеств признаков порождает их
-элементных частых множеств признаков порождает их 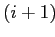 -надмножества и возвращает только множество потенциально частых кандидатов.
-надмножества и возвращает только множество потенциально частых кандидатов.
Алгоритм Apriori был разработан для извлечения частых множеств признаков из данных о покупках, которые обычно являются разреженными и слабо коррелированными. Для таких данных число частых множеств признаков невелико, и алгоритм работает очень хорошо. Позднее, когда возникла необходимость поиска частых множеств признаков в плотных, сильно коррелированных данных, оказалось, что Apriori неэффективно работает на таких массивах. Как следствие, для решения проблемы были предложены различные варианты оптимизации и расширения исходного алгоритма (например, Apriori-Close, Pascal, Zart).
2.5.3. Связь частых замкнутых множеств признаков и ФАП
В сообществе ФАП хорошо известен тот факт, что семейства частых множеств обладают решеточной структурой (см., например, [59]). Приведем определение решетки замкнутых частых множеств признаков.
Определение 2.31
Пусть дан формальный контекст
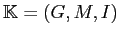
и множество всех частых замкнутых множеств признаков
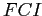
для
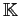
,
тогда
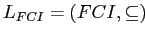
образует полную решетку, называемую решеткой частых замкнутых множества признаков.
Отметим, что такая решетка изоморфна решетке понятий соответствующего контекста, а ее элементы совпадают с содержаниями понятий. Если задать ограничение на величину поддержки, то мы получим так называемую решетку-айсберг, т.е. верхнюю часть 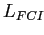 .
Подробнее о решетках-айсбергах и связи
.
Подробнее о решетках-айсбергах и связи 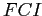 и формальных понятий см. [72].
и формальных понятий см. [72].
2.6. Ассоциативные правила в контексте бикластеризации
В сообществе DataMining ассоциативные правила являются, пожалуй, одним из наиболее востребованных инструментов для исследования признаковых зависимостей. И хотя ассоциативные правила явно не относятся к методам бикластеризации мы не только укажем на их тесную связь с ФАП, но и покажем, как менее "жесткие", чем формальные понятия, бикластеры могут быть получены с помощью ассоциативных правил.
Одной из первых работ, положившей начало применению ассоциативных правил промышленного масштаба в середине 90-х годов прошлого века, была [10]. Однако ранее в анализе формальных понятий изучались так называемые частичные импликации [52], которые фактически и были переоткрыты как ассоциативные правила в сообществе DataMining. Появление раздела, посвященного задаче поиска ассоциаций, обосновано также тем, что, оказывается, с бискластеризацией их связывают не только теоретические рассмотрения, но и общие прикладные задачи.
2.6.1. Ассоциативные правила: общий взгляд
Дадим основные определения.
Определение 2.32
Пусть дан контекст
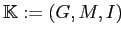
,
где
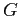
— множество объектов,
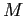
— множество признаков (items),
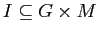
— отношение инцидентности.
Ассоциативным правилом контекста
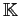
называется выражение вида
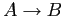
,
где
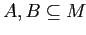
.
Определение 2.33
Поддержкой (support) ассоциативного правила
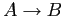
называется величина
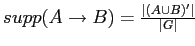
.
Значение
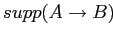 показывает, какая доля объектов
показывает, какая доля объектов 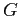 содержит
содержит 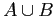 .
Часто поддержку выражают в
.
Часто поддержку выражают в 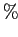 .
.
Определение 2.34
Достоверностью (confidence) ассоциативного правила
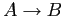
называется величина
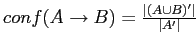
.
Значение
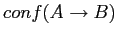 показывает, какая доля объектов, обладающих
показывает, какая доля объектов, обладающих 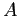 ,
также содержит
,
также содержит 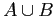 .
Величину достоверности также часто выражают в
.
Величину достоверности также часто выражают в 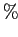 .
.
Для аналитика обычно интересны ассоциативные правила с поддержкой supp и степенью достоверности conf не ниже заданных значений min_supp и min_conf соответственно. Для решения этой задачи можно построить все частые множества признаков. Напомним, что множество признаков
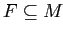 называется частым, если оно принадлежит большому числу объектов, то есть
называется частым, если оно принадлежит большому числу объектов, то есть
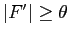 ,
где
,
где 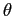 — некоторый порог. Для этапа нахождения частых множеств признаков можно использовать алгоритм Apriori.
— некоторый порог. Для этапа нахождения частых множеств признаков можно использовать алгоритм Apriori.
Частое ассоциативное правило получают из частого подмножества признаков 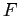 разбиением его на два подмножества
разбиением его на два подмножества 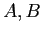 ,
то есть
,
то есть
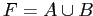 ,
,
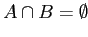 ,
одно из которых (например,
,
одно из которых (например, 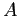 )
объявляют посылкой, а другое (
)
объявляют посылкой, а другое (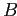 ) — заключением ассоциативного правила. При таком разбиении
) — заключением ассоциативного правила. При таком разбиении 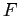 на
на 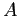 и
и 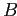 нужно проследить за тем, чтобы достоверность ассоциативного правила
нужно проследить за тем, чтобы достоверность ассоциативного правила 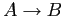 была не ниже заданной.
была не ниже заданной.
Отметим, что ассоциативные правила при значениях
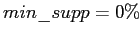 и
и
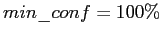 являются импликациями рассматриваемого контекста. Иногда ассоциативные правила записывают в форме
являются импликациями рассматриваемого контекста. Иногда ассоциативные правила записывают в форме
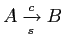 ,
где c и s — confidence и support данного правила соответственно.
,
где c и s — confidence и support данного правила соответственно.
2.6.2. Связь ассоциативных правил и бикластеризации
Пусть даны два соседних формальных понятия в смысле отношения покрытия
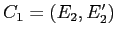 и
и
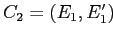 ,
т.е.
,
т.е.
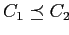 .
Тогда ассоциативное правило
.
Тогда ассоциативное правило
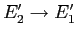 определяет бикластер
определяет бикластер
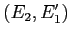 .
Учтем, что
.
Учтем, что
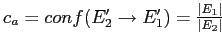 — достоверность признакового ассоциативного правила для этих понятий, а
— достоверность признакового ассоциативного правила для этих понятий, а
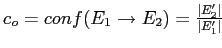 — достоверность объектного ассоциативного правила. Тогда максимальное число незаполненных (нулевых) ячеек в таком бикластере определяется величиной
— достоверность объектного ассоциативного правила. Тогда максимальное число незаполненных (нулевых) ячеек в таком бикластере определяется величиной
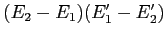 .
Выразим относительную величину для этой оценки, которую мы будем назвать разреженностью бикластера, через достоверность правил:
.
Выразим относительную величину для этой оценки, которую мы будем назвать разреженностью бикластера, через достоверность правил:
очевидно, что
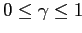 .
.
Назад Содержание Вперёд