2008 г.
Методы бикластеризации для анализа интернет-данных
Дмитрий Игнатов,
кафедра анализа данных и искусственного интеллекта ГУ-ВШЭ
Назад Содержание Вперёд
2.5. Частые (замкнутые) множества признаков
Задача поиска частых множеств признаков (frequent itemsets mining) является одной из центральных тем в DataMining. Первоначально необходимость поиска частых множества признаков возникла при выявлении часто покупаемых вместе товаров в базах данных транзакций. Неформально ее можно описать так: дана большая база данных транзакций (покупок); необходимо найти все часто покупаемые наборы товаров, число покупок которых превышает заданный пользователем порог.
В настоящее время набор приложений, в которых основным этапом является построение частых множеств признаков, существенно расширился, например, это поиск ассоциативных правил (см. раздел 2.6), сильных правил (strong rules), корреляций, секвенциальных правил, эпизодов (episodes), многомерных образов (multidimensional patterns) и многие другие задачи анализа данных [36].
Среди частых множеств признаков выделяют так называемые частые замкнутые множества признаков, которые полезны для их более компактного представления. Такое представление осуществляется без потерь информации о поддержке собственных частых подмножеств данных частых замкнутых множеств признаков.
Хорошо известным фактом для сообщества DataMining является то, что все замкнутые частые множества признаков (т.е. при 
)
образуют решетку; эта решетка изоморфна решетке понятий контекста для соответствующей базы данных. Более того, все замкнутые множества признаков образуют в точности решетку содержаний понятий такого контекста [86].
Ниже будут даны основные определения; для единства изложения и общности понимания которых будем использовать терминологию, принятую в ФАП. Приведем также классический алгоритм для поиска частых множеств признаков Apriori [9], который не утратил своей актуальности и стал отправной точкой для огромного числа других алгоритмов. Обсудим также связь ФАП и поиска частых замкнутых множеств признаков, которая позволяет рассматривать оба метода в контексте бикластеризации.
2.5.1. Основные определения и свойства
Дадим определение частого множества признаков в терминах ФАП.
Определение 2.25
Пусть дан формальный контекст
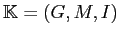
. Множество признаков
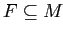
называется
частым множеством признаков, если
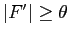
, где
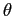
— заданный числовой порог
.
Здесь контекст
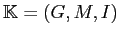представляет собой объектно-признаковую таблицу, которую можно интерпретировать как базу данных покупок, 
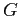— множество транзакций, а 
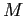— множество товаров.
Ключевым понятием для данной задачи является поддержка.
Определение 2.26
Пусть дан формальный контекст
.
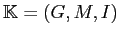
Поддержкой множества признаков
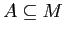
называется величина
.
Значение 
показывает, какая доля объектов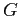
содержит 
.
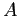Часто поддержку выражают в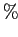 
.
Если задано значение минимальной поддержки 
,
то Определение 2.25 можно переписать следующим образом.
Определение 2.27
Пусть дан формальный контекст
.
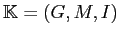
Множество признаков
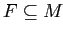
называется
частым множеством признаков, если
.
Дадим определения частых замкнутых множеств признаков и максимальных частых множеств признаков.
Определение 2.28
Пусть дан формальный контекст
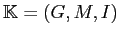
. Множество признаков
называется
частым замкнутым множеством признаков, если
и не существует
,
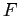
такого что
и
.
Используя оператор замыкания, можно дать следующее определение, эквивалентное 2.28.
Определение 2.29
Пусть дан формальный контекст
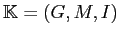
. Множество признаков
называется
частым замкнутым множеством признаков, если
и
.
Определение 2.30
Пусть дан формальный контекст
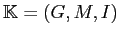
. Множество признаков
называется
максимальным частым множеством признаков, если
и не существует
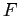
, такого что
и
.
Пусть 
— множество всех частых множеств признаков,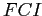 
— множество всех частых замкнутых множеств признаков, 
— множество всех максимальных частых множеств признаков. Тогда, очевидно, выполнено следующее соотношение
.
Как уже было отмечено выше, частые замкнутые множества позволяют компактно представлять все множество частых признаков без потерь информации об их частоте. Максимальные множества признаков, хотя и являются компактным представлением даже меньшего размера, не позволяют вычислить поддержку всех частых множеств признаков.
Тем не менее, применение максимальных частых множеств признаков оправдано для плотных контекстов, например, для данных телекоммуникационных компаний, данных переписи, данных последовательностей, изучаемых в биоинформатике. Это связано с тем, что для частого множества признаков длины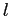 
приходится вычислять 
его частых подмножеств на ранних этапах работы алгоритмов, таких как Apriori. Поэтому MFI помогают понять структуру извлекаемых множеств признаков в указанных выше задачах (в случае плотных контекстов, для которых длина частых множеств признаков довольно часто равна 30-40), в то время как поиск всех частых множеств признаков оказывается невозможным.
Отметим два важных для практической реализации свойства частых множеств признаков.
Свойство 2.1 (нисходящее замыкание).
Все подмножества частого множества признаков являются частыми.
Название свойства "нисходящее замыкание" (downward closure) обязано тому, что множество частых множеств признаков замкнуто по вложению.
Свойство 2.2 (антимонотонность).
Все надмножества множества признаков, не являющего частым, не частые.
Свойство 2.1 позволяет создавать алгоритмы, использующие поуровневый поиск частых множеств признаков. А свойство антимонотонности помогает сократить число шагов такого поиска, т.е. не рассматривать надмножества множеств признаков, не являющихся частыми. Алгоритмы поиска частых множеств признаков, использующие эти два свойства, называются поуровневыми (levelwise).
Назад Содержание Вперёд
Виртуальные VPS серверы в РФ и ЕС
Пиво, Чипсы
🔥 VPS до 5.7 ГГц под любые задачи с AntiDDoS в 7 локациях
