Асинхронные тестовые сценарии
Генерация тестовых данных для асинхронных систем
В данном разделе мы рассмотрим проблему генерации тестовых данных для асинхронных систем. Решение этой проблемы сильно осложняется большой временной сложностью алгоритмов оценки корректности поведения асинхронных систем. Область применимости этих алгоритмов ограничена асинхронными моделями поведения, состоящими из нескольких десятков взаимодействий.
Одного теста такого размера явно не достаточно для достижения приемлемого качества тестирования. Построение наборов независимых тестов небольшого размера приведет к потере одного из основных достоинств технологии UniTesK - автоматическому построению сложных последовательностей тестовых воздействий.
Компромиссное решение, позволяющее совместить генерацию тестовых последовательностей с ограничениями на размеры модели поведения, подвергающейся оценки корректности, было предложено в работе [27]. Идея этого подхода заключается в использовании автоматных тестовых сценариев для построения обхода графа, в котором каждой дуге приписан асинхронный тест небольшого размера. Для реализации такого подхода требуется, чтобы целевая система после получения любого набора асинхронных воздействий за конечное время переходила в состояние, в котором она не должна выдавать ни одной асинхронной реакции до получения следующего воздействия.
С учетом этого ограничения данный подход позволяет сохранить автоматическое построение сложных последовательностей тестовых воздействий, несмотря на ограниченную применимость алгоритма оценки корректности поведения.
В последующих разделах мы рассмотрим вопрос построения тестов для систем с асинхронным интерфейсом более формально.
Взаимодействующие автоматы
Определение 13.
Взаимодействующим автоматом будем называть шестерку ( S, s0, X, Y, E, Q ), где
- S - множество состояний,
- s0
 S - начальное состояние,
S - начальное состояние,
- X - множество стимулов,
- Y - множество реакций,
- E
 S x ( X
S x ( X  Y
Y  {τ} ) x S - множество переходов, которые мы будем называть
{τ} ) x S - множество переходов, которые мы будем называть
- посылающими, если второй элемент перехода является стимулом,
- принимающими, если второй элемент перехода является реакцией,
- внутренним, если второй элемент перехода является τ;
- Q
 S - множество заключительных состояний.
S - множество заключительных состояний.
Взаимодействующий автомат может посылать стимулы и получать реакции, изменяя при этом свое состояние. При возможности выбора очередного перехода этот выбор осуществляется в зависимости от доступности реакций для получения. Выбор перехода среди различных доступных переходов осуществляется недетерминировано.
Первый элемент перехода взаимодействующего автомата мы будем называть пресостоянием перехода, второй - сообщением, а третий - постсостоянием.
Заметим, что множества стимулов и реакций могут пересекаться (X 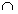 Y ≠ Ø), и поэтому в определении множества переходов используется операция дизъюнктивного объединения. Для обозначения того факта, что сообщение является стимулом мы будем использовать символ !, помещаемый следом за элементом множества X (например, x!), а для обозначения принадлежности сообщения к множеству реакций будет использоваться символ ?: (например, y?).
Y ≠ Ø), и поэтому в определении множества переходов используется операция дизъюнктивного объединения. Для обозначения того факта, что сообщение является стимулом мы будем использовать символ !, помещаемый следом за элементом множества X (например, x!), а для обозначения принадлежности сообщения к множеству реакций будет использоваться символ ?: (например, y?).
Конечная последовательность переходов ( e1, e2, …, en ) взаимодействующего автомата A = ( S, s0, X, Y, E, Q ) называется путем, если для каждого i = 1, …, n-1 постсостояние перехода ei совпадает с пресостоянием перехода ei+1. При этом мы будем говорить, что путь ведет из пресостояния перехода e1 в постсостояние перехода en.
Бесконечным путем мы будем называть бесконечную последовательность переходов, любой префикс которой является конечным путем.
Путь ( e1, e2, …, en ) взаимодействующего автомата A = ( S, s0, X, Y, E, Q ) называется функционированием, если пресостоянием перехода e1 является начальное состояние s0, а постсостояние перехода en принадлежит множеству конечных состояний Q.
Линейно-упорядоченное мультимножество стимулов и реакций ( T,  ) называется трассой взаимодействующего автомата A = ( S, s0, X, Y, E, Q ), если существует такое функционирование ( e1, e2, …, en ) автомата A, что
) называется трассой взаимодействующего автомата A = ( S, s0, X, Y, E, Q ), если существует такое функционирование ( e1, e2, …, en ) автомата A, что
- мультимножество T совпадает с мультимножеством всех сообщений функционирования ( e1, e2, …, en ), отличающихся от τ;
- порядок
 совпадает с порядком этих сообщений в функционировании ( e1, e2, …, en ).
совпадает с порядком этих сообщений в функционировании ( e1, e2, …, en ).
Множество всех возможных трасс взаимодействующего автомата A мы будем обозначать Traces(A).
Определение 14.
Дадим определение распределенного взаимодействующего автомата в рекурсивной форме.
- взаимодействующий автомат A = ( S, s0, X, Y, E, Q ) является распределенным взаимодействующим автоматом;
- если A1, A2, …, An - распределенные взаимодействующие автоматы, а M - множество сообщений, то система взаимодействующих автоматов с множеством внутренних сообщений M (A1,A2,…,An)\M является распределенным взаимодействующим автоматом.
Множеством стимулов распределенного взаимодействующего автомата DA будем называть
- множество стимулов X, если автомат DA является взаимодействующим автоматом A = ( S, s0, X, Y, E, Q ),
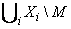 , если автомат DA является системой взаимодействующих автоматов A1, A2, …, An с множеством внутренних сообщений M.
, если автомат DA является системой взаимодействующих автоматов A1, A2, …, An с множеством внутренних сообщений M.
Аналогично, множеством реакций распределенного взаимодействующего автомата DA будем называть
- множество реакций Y, если автомат DA является взаимодействующим автоматом A = ( S, s0, X, Y, E, Q ),
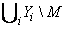 , если автомат DA является системой взаимодействующих автоматов A1, A2, …, An с множеством внутренних сообщений M.
, если автомат DA является системой взаимодействующих автоматов A1, A2, …, An с множеством внутренних сообщений M.
В системе взаимодействующих автоматов с множеством внутренних сообщений M все взаимодействующие автоматы обмениваются сообщениями из множества M только между собой и не могут обмениваться ими с окружением.
Предположим, что взаимодействующий автомат A = ( S, s0, X, Y, E, Q ) входит в состав системы взаимодействующих автоматов SA = (A1,A2,…,An)\M. Тогда мы будем говорить, что сообщение m  X
X  Y автомата A сокрыто в SA, если m
Y автомата A сокрыто в SA, если m  M и не существует системы взаимодействующих автоматов SA' = (A'1,A'2,…,A'n')\M', входящей в SA, такой что m
M и не существует системы взаимодействующих автоматов SA' = (A'1,A'2,…,A'n')\M', входящей в SA, такой что m  M' и A входит в состав SA'.
M' и A входит в состав SA'.
Предположим, что взаимодействующий автомат A = ( S, s0, X, Y, E, Q ) входит в состав распределенного взаимодействующего автоматов DA. Переходы автомата A ( s1, m, s2 )  E будем называть внутренними для DA, если сообщение m сокрыто в одной из систем взаимодействующих автоматов, входящей в состав DA. В противном случае, переходы будем называть внешними для DA.
E будем называть внутренними для DA, если сообщение m сокрыто в одной из систем взаимодействующих автоматов, входящей в состав DA. В противном случае, переходы будем называть внешними для DA.
Функционированием распределенного взаимодействующего автомата DA называется тройка ( E,  , μ ), где
, μ ), где
- E - набор функционирований { ( ei,1, ei,2, …, ei,n(i) ) } всех взаимодействующих автоматов, входящих в DA;
 - частичный порядок на множестве всех переходов { ei,j }i, j=1,…,n(i) набора E;
- частичный порядок на множестве всех переходов { ei,j }i, j=1,…,n(i) набора E;
- μ : { ei,j }
 { ei,j } - отображение на этом же множестве переходов;
{ ei,j } - отображение на этом же множестве переходов;
при условии, что E,  и μ удовлетворяют следующим ограничениям:
и μ удовлетворяют следующим ограничениям:
- областью определения μ является множество всех принимающих переходов ei,j = ( s1, m?, s2 ) автомата A, сообщение m которых сокрыто в некоторой системе взаимодействующих автоматов SA, входящей в состав DA;
- для каждого такого перехода ei,j = ( s1, m?, s2 ) значением μ(ei,j) является посылающий переход ei',j' = ( s'1, m!, s'2 ) автомата A', входящего в состав той же системы взаимодействующих автоматов SA, но не совпадающего с A (A ≠ A');
- частичный порядок
 сохраняет порядок переходов, относящихся к функционированию одного взаимодействующего автомата, то есть
сохраняет порядок переходов, относящихся к функционированию одного взаимодействующего автомата, то есть
 ei,j, ei',j'
ei,j, ei',j'  { ei,j } (i = i')
{ ei,j } (i = i') 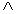 (j < j')
(j < j')  ei,j
ei,j  ei',j';
ei',j';
- переходы, связанные отношением μ, являются неразличимыми относительно частичного порядка
 , то есть
, то есть
 ei,j, ei',j'
ei,j, ei',j'  { ei,j } ei',j' = μ(ei,j)
{ ei,j } ei',j' = μ(ei,j) 
 e
e  { ei,j } ( (e
{ ei,j } ( (e  ei,j)
ei,j)  (e
(e  ei',j') )
ei',j') )  ( (ei,j
( (ei,j  e)
e)  (e i',j'
(e i',j'  e) ).
e) ).
Распределенный взаимодействующий автомат функционирует таким образом, что его компоненты обмениваются внутренними сообщениями между собой, а остальными сообщениями как между собой, так и с окружением. Функционирование такого автомата состоит из набора функционирований составляющих его взаимодействующих автоматов, а также из частичного порядка, определяющего порядок осуществления переходов во времени, и отображения μ, связывающее каждое получение внутреннего сообщения с его посылкой.
Заметим, что одной посылке сообщения может соответствовать несколько получений этого сообщения, то есть посылка сообщений может быть широковещательной. Все взаимодействия между автоматами осуществляются синхронным образом, а асинхронные взаимодействия должны моделироваться явно, например, при помощи дополнительного автомата моделирующего работу канала связи или буфера.
Частично упорядоченное мультимножество стимулов и реакций ( T,  T ) называется трассой распределенного взаимодействующего автомата DA, если существует такое функционирование ( E,
T ) называется трассой распределенного взаимодействующего автомата DA, если существует такое функционирование ( E,  , μ ) автомата DA, что
, μ ) автомата DA, что
Множество всех возможных трасс распределенного взаимодействующего автомата DA мы будем обозначать Traces(DA).
Асинхронные функции
Для вычисления функций в распределенных взаимодействующих автоматах реализуется посредством использования выделенных взаимодействующих автоматов, получающих входные параметры функции и возвращающих результат.
Асинхронной функцией AF из множества входных значений IS во множество выходных значений OS называется взаимодействующий автомат SA = ( S, s0, X, Y, E, Q ), в котором
- PY = { callAF,is | is
 IS }
IS }  Y - множество входных значений параметризует выделенное подмножество реакций автомата,
Y - множество входных значений параметризует выделенное подмножество реакций автомата,
- RX = { resultAF,os | os
 OS }
OS }  X - множество выходных значений параметризует выделенное подмножество стимулов автомата,
X - множество выходных значений параметризует выделенное подмножество стимулов автомата,
- RX
 PY = Ø,
PY = Ø,
 ( s, m, s' )
( s, m, s' )  E (s = s0)
E (s = s0)  m
m  PY,
PY,
 ( s, m, s' )
( s, m, s' )  E m
E m  PY
PY 
 m'
m'  PY
PY  s''
s''  S: ( s, m', s'' )
S: ( s, m', s'' )  E,
E,
 ( s, m, s' )
( s, m, s' )  E (m
E (m  RX)
RX) 
 ( s', m', s'' )
( s', m', s'' )  E m'
E m'  PY,
PY,
 пути ( e1, e2, …, en ) в SA (n > 1)
пути ( e1, e2, …, en ) в SA (n > 1)
e1 = ( s1, py1, s'1 )  en = ( sn, pyn, s'n )
en = ( sn, pyn, s'n ) 
 j
j  { 2, ..., n-1 } ej = ( sj, rx, s'j ),
{ 2, ..., n-1 } ej = ( sj, rx, s'j ),
 q
q  Q
Q  ( s, m, s' )
( s, m, s' )  E (s' = q)
E (s' = q)  m
m  RX.
RX.
Данные ограничения определяют ту специфическую роль, которую играют сообщения из PY и RX в работе автомата SA. Эта роль заключается в том, что функционирование автомата SA состоит из последовательных циклов, каждый из которых начинается получением параметризующей реакции callAF,ip и завершается посылкой результирующего стимула resultAF,op. Внутри этого цикла автомат SA произвольным образом взаимодействует со своим окружением, но только посредством сообщений, не входящих в PY  RX.
RX.
Множество всех асинхронных функций, у которых множество входных значений равно IS, а множество выходных значений равно OS, мы будем обозначать как Ã(IS,OS).
Чтобы работа распределенного взаимодействующего автомата завершилась, необходимо, чтобы все составляющие его автоматы перешли в заключительное состояние. Для этого вместо асинхронных функций обычно используют их замыкания по выделенному множеству терминирующих реакций.
Замыканием взаимодействующего автомата ( S, s0, X, Y, E, Q ) по множеству реакций R мы будем называть взаимодействующий автомат ( S', s'0, X', Y', E', Q' ), в котором
- S' = S
 {final},
{final},
- s'0 = s0,
- X' = X,
- Y' = Y
 R,
R,
- E' = E
 { ( s, r, final ) |
{ ( s, r, final ) |  s
s  S,
S,  r
r  R },
R },
- Q' = Q
 {final}.
{final}.
Замыкание взаимодействующего автомата дополняет исходный автомат специальным завершающим состоянием и множеством переходов, ведущих в это состояние изо всех остальных состояний по получению реакции из множества R.
Асинхронные тесты
Асинхронным тестом целевой системы с асинхронным интерфейсом
( X, Y, Z
) называется конечное или бесконечное частично упорядоченное мультимножество асинхронных взаимодействий
( P,
 )
), которое совпадает с моделью поведения целевой системы в ходе этого теста.
Асинхронный тест ( P,  ) целевой системы с асинхронным интерфейсом ( X, Y, Z ) будем называть успешным относительно асинхронной модели требований A = ( V, X, Y, Z, E ) с начальным состоянием v0
) целевой системы с асинхронным интерфейсом ( X, Y, Z ) будем называть успешным относительно асинхронной модели требований A = ( V, X, Y, Z, E ) с начальным состоянием v0  V, если модель поведения в ходе теста ( P,
V, если модель поведения в ходе теста ( P,  ) удовлетворяет модели требований A с начальным состоянием v0. В противном случае, тест будет называться неуспешным.
) удовлетворяет модели требований A с начальным состоянием v0. В противном случае, тест будет называться неуспешным.
Определение 15.
Асинхронным тестовым сценарием для целевой системы с асинхронным интерфейсом ( X, Y, Z ) называется распределенный взаимодействующий автомат DA, в котором
- множество стимулов совпадает с X;
- множество реакций совпадает с Y
 Z;
Z;
- для любого взаимодействующего автомата A' = ( S', s'0, X', Y', E', Q' ), входящего в состав DA, для любого внешнего для DA посылающего перехода ( s1, x!, s2 )
 E', сообщение x которого принадлежит X
E', сообщение x которого принадлежит X 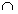 X', любой переход ( s2, m, s3 )
X', любой переход ( s2, m, s3 )  E', начинающийся в состоянии s2, является принимающим и внешним для DA, а его сообщение m принадлежат множеству Y;
E', начинающийся в состоянии s2, является принимающим и внешним для DA, а его сообщение m принадлежат множеству Y;
- для любого взаимодействующего автомата A' = ( S', s'0, X', Y', E', Q' ), входящего в состав DA, для любого внешнего для DA принимающего перехода ( s2, y?, s3 )
 E', сообщение y которого принадлежит Y
E', сообщение y которого принадлежит Y 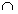 Y', любой переход ( s1, m, s2 )
Y', любой переход ( s1, m, s2 )  E', завершающийся в состоянии s2, является посылающим и внешним для DA.
E', завершающийся в состоянии s2, является посылающим и внешним для DA.
Состояния взаимодействующих автоматов, из которых выходят только принимающие переходы, помеченные сообщениями из Y, будут далее называться промежуточными.
Асинхронный тестовый сценарий предназначен для управлением процессом тестирования систем с асинхронным интерфейсом. Такой тестовый сценарий подает тестовые стимулы целевой системе и получает от нее непосредственные и отложенные реакции, используя эту информацию для продолжения тестирования.
Множество всех асинхронных тестовых сценариев для целевой системы с асинхронным интерфейсом ( X, Y, Z ) будем обозначать символом 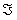 ( X, Y, Z ).
( X, Y, Z ).
Асинхронный тест ( P,  ) называется результатом применения тестового сценария DA для целевой системы с асинхронным интерфейсом ( X, Y, Z ) к соответствующей целевой системе, если ( P,
) называется результатом применения тестового сценария DA для целевой системы с асинхронным интерфейсом ( X, Y, Z ) к соответствующей целевой системе, если ( P,  )
)  Traces(DA).
Traces(DA).
Асинхронный тестовый сценарий определяет правила посылки тестовых стимулов, которые могут зависеть от ответа целевой системы. Результатом работы сценария является асинхронный тест, состоящий из набора взаимодействий с целевой системой и информации о порядке, в котором происходили эти взаимодействия. Этот порядок в точности соответствует порядку взаимодействий между тестовым сценарием и целевой системой, наблюдаемому в процессе работы тестового сценария.
При наличии некоторой среды между тестовой системой и целевой системой, например, сетевого соединения, которое не гарантирует сохранения порядка сообщений, предполагается, что эта среда включается в тестовый сценарий и моделируется в нем явно. В качестве альтернативы включения среды между тестовой системой и целевой системой в состав тестового сценария можно использовать включение этой среды в состав целевой системы, но в этом случае все требования к поведению целевой системы необходимо формулировать с учетом поведения этой среды.
Определение 16.
Механизмом построения асинхронного тестового сценария будем называть функцию, значением которой является асинхронный тестовый сценарий.
Также как и для обычных тестовых сценариев, для асинхронных тестовых сценариев мы определим автоматный механизм их построения, который обеспечивает автоматическое формирование последовательности тестовых воздействий на основе обхода ориентированного графа.
Автоматный механизм построения асинхронного тестового сценария
Асинхронным автоматным тестовым сценарием для целевой системы с асинхронным интерфейсом
( X, Y, Z
) называется пятерка
( DA, A
fsm, IG, vg
0, α
), где
- DA - асинхронный тестовый сценарий для целевой системы с асинхронным интерфейсом ( X, Y, Z ),
- Afsm = ( Sfsm, s0, Xfsm, Yfsm, Efsm, Qfsm ) - выделенный взаимодействующий автомат, входящий в состав DA, и называемый ведущим автоматом асинхронного тестового сценария DA,
- IG = ( VG, XG, π ) - неизбыточное описание ориентированного графа, называемого графом сценария,
- vg0
 VG - начальное состояние графа сценария,
VG - начальное состояние графа сценария,
- α - неизбыточный алгоритм движения по графу сценария;
и для которой выполнены следующие ограничения:
- Sfsm = ( VG x EG* x (XG
 { ε }) )
{ ε }) )  { final } - состояние ведущего автомата является либо выделенным состоянием final, либо содержит:
{ final } - состояние ведущего автомата является либо выделенным состоянием final, либо содержит:
- текущую вершину графа сценария vg,
- пройденный маршрут в графе сценария path (здесь множество EG* обозначает множество всех конечных списков элементов из множества дуг EG = VG x XG x VG),
- последний посланный стимул графа, на который не был получен ответ, либо ε, обозначающее отсутствие такового стимула;
- s0 = ( vg0,
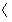
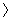 , ε ) - начальное состояние ведущего автомата состоит из
, ε ) - начальное состояние ведущего автомата состоит из
- начальной вершины графа сценария,
- пройденного пути, равного пустому списку,
- специального значения ε;
- Xfsm = { startvg,xg | vg
 VG, xg
VG, xg  XG }
XG }  { stop } - множество стимулов ведущего автомата состоит из набора стимулов, помеченных вершиной и стимулом графа, и из дополнительного стимула, символизирующего завершение работы, причем все эти стимулы являются внутренними для DA;
{ stop } - множество стимулов ведущего автомата состоит из набора стимулов, помеченных вершиной и стимулом графа, и из дополнительного стимула, символизирующего завершение работы, причем все эти стимулы являются внутренними для DA;
- Yfsm = { finishvg | vg
 VG }
VG }  { abort } - множество реакций ведущего автомата состоит из набора реакций, помеченных вершинами графа, и из дополнительной реакции, символизирующей аварийное завершение работы, причем все эти реакции являются внутренними для DA;
{ abort } - множество реакций ведущего автомата состоит из набора реакций, помеченных вершинами графа, и из дополнительной реакции, символизирующей аварийное завершение работы, причем все эти реакции являются внутренними для DA;
- Efsm = { ( ( vg, path, ε ), startvg,xg, ( vg, path, xg ) ) | xg = α( IG, vg, path ) }

{ ( ( vg, path, ε ), stop, final ) | α( IG, vg, path ) = τ }

{ ( ( vg, path, xg ), finishvg*, ( vg', path', ε ) |
vg' = vg* 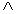
path' = path ^ ( vg, xg, vg' )
}

{ ( ( vg, path, xg ), abort, final ) }
- Qfsm = { final } - множество заключительных состояний ведущего автомата состоит из единственного состояния final.
Автоматным механизмом построения асинхронного тестового сценария называется функция, которая преобразует асинхронный автоматный тестовый сценарий ( DA, Afsm, IG, vg0, α ) в асинхронный тестовый сценарий DA.
Работа автоматного тестового сценария устроена следующим образом. Граф сценария описывает некоторым образом пространство тестовых ситуаций. Ведущий автомат двигается по данному графу, используя заданный алгоритм движения.
Алгоритм движения выбирает стимул графа, который необходимо подать в текущей вершине. Ведущий автомат посылает сообщение, соответствующее текущей вершине и выбранному стимулу. Это сообщение обрабатывается другими взаимодействующими автоматами, входящими в состав DA, и преобразуется в набор воздействий на целевую систему. По завершении обработки этого сообщения, ведущему автомату посылается либо новая вершина графа, либо уведомление об аварийном завершении работы. В первом случае, ведущий автомат повторяет рассмотренный цикл до тех пор, пока алгоритм движения не завершит свою работу. Во втором случае, работа тестового сценария завершается.
Асинхронные сценарные функции
Для описания стимулов графа автоматного сценария в асинхронном случае так же, как и в синхронном, используется понятие сценарной функции. В данном случае, в качестве сценарной функции выступает обычная асинхронная функция, а множество допустимых стимулов определяется на основе множества ее входных параметров.
Асинхронной сценарной функцией мы будем называть асинхронную функцию, в которой множество входных значений может быть произвольным, а множество выходных значений Bool состоит из двух элементов true и false.
Множество всех асинхронных сценарных функций, у которых множество входных значений равно IS, мы будем обозначать как Σ(IS).
Асинхронным автоматным тестовым сценарием со сценарными функциями для целевой системы с асинхронным интерфейсом ( X, Y, Z ) называется семерка ( DA, Afsm, VG, XG, vg0, α, 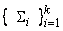 ), где
), где
- DA - асинхронный тестовый сценарий для целевой системы с асинхронным интерфейсом ( X, Y, Z ),
- Afsm ( Sfsm, s0, Xfsm, Yfsm, Efsm, Qfsm ) - выделенный взаимодействующий автомат, входящий в состав DA, и называемый ведущим автоматом асинхронного тестового сценария DA,
- VG - множество состояний графа сценария,
- XG - множество стимулов графа сценария,
- vg0 - начальное состояние графа сценария,
- α - неизбыточный алгоритм движения по графу сценария,
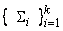 - конечный набор асинхронных сценарных функций Σi = ( Si, s0,i, Xi, Yi, Ei, Qi )
- конечный набор асинхронных сценарных функций Σi = ( Si, s0,i, Xi, Yi, Ei, Qi )  Σ(ISi);
Σ(ISi);
и для которой выполнены следующие ограничения:
- замыкания взаимодействующих автоматов Σi по множеству { stop, abort } входят в состав DA, причем все эти вхождения и вхождение Afsm в DA различаются между собой,
 i
i  { 1, …, k } ISi
{ 1, …, k } ISi  VG x XG,
VG x XG,
 i, j
i, j  { 1, …, k } i ≠ j
{ 1, …, k } i ≠ j  XGi
XGi 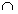 XGj = Ø,
XGj = Ø,
где XGi = { xg  XG |
XG | 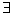 vg
vg  VG: ( vg, xg )
VG: ( vg, xg )  ISi },
ISi },
- Xfsm =
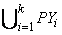
 { stop }, где PYi = { calli,is | is
{ stop }, где PYi = { calli,is | is  ISi },
ISi },
- сообщения из
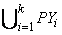 присутствуют только в ведущем автомате и автоматах-сценарных функциях,
присутствуют только в ведущем автомате и автоматах-сценарных функциях,
- пятерка ( DA, Afsm, IG, vg0, α ), в которой IG состоит из
- множества состояний графа сценария VG,
- множества стимулов графа сценария XG,
- функции π: π(vg) = { xg
 XG |
XG | 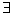 i
i  { 1, …, k }: ( vg, xg )
{ 1, …, k }: ( vg, xg )  ISi },
ISi },
является асинхронным автоматным тестовым сценарием для целевой системы с асинхронным интерфейсом ( X, Y, Z ).
Стационарное тестирование асинхронных систем
Тестирование систем с асинхронным интерфейсом значительно осложнено большой временной сложностью алгоритмов оценки корректности поведения тестируемой системы. Область применимости этих алгоритмов ограничена асинхронными моделями поведения, состоящими из нескольких десятков взаимодействий.
В большинстве случаев одного теста такого размера оказывается недостаточно для достижения требуемого качества тестирования. Как следствие, появляется необходимость в построении набора тестов небольшого размера. Если разрабатывать такие наборы тестов независимо друг от друга, то при этом теряется одно из основных достоинств технологии UniTesK - автоматическое построении сложных последовательностей тестовых воздействий.
Компромиссное решение, позволяющее совместить генерацию тестовых последовательностей с ограничениями на размеры модели поведения, подвергающейся оценки корректности, было предложено в работе [27]. Идея этого подхода заключается в использовании автоматных тестовых сценариев для построения обхода графа, в котором каждой дуге соответствует асинхронный тестовый сценарий небольшого размера.
Оценка корректности поведения целевой системы, в этом случае, выполняется каждый раз после завершения работы локального тестового сценария. Так как размеры такого сценария небольшие, то алгоритм оценки корректности поведения обрабатывает его результаты за приемлемое время. По завершении этой проверки автоматный тестовый сценарий продолжает обход графа, то есть выбирает следующую дугу и выполняет соответствующий локальный тестовый сценарий.
В результате, такое решение сохраняет генерацию последовательности тестовых воздействий, позволяющую автоматически выполнять набор тестовых воздействий в различных состояниях графа, и в то же время обходит ограничения алгоритма оценки корректности поведения.
В настоящей работе мы ограничимся рассмотрением случае, когда во время проверки корректности поведения после завершения локального сценария тестируемая система не выполняет никаких активных действий. Это означает, что при корректном поведении целевой системы ожидается, что после завершения работы локального тестового сценария целевая система не будет посылать никаких отложенных реакций. Или другими словами, предполагается, что тестируемая система находится в стационарном состоянии.
Определение 17.
Стационарными состояниями асинхронной модели требований ( V, X, Y, Z, E ) называются такие состояния v  V, из которых выходят только переходы, помеченные стимулом и непосредственной реакцией, то есть
V, из которых выходят только переходы, помеченные стимулом и непосредственной реакцией, то есть  ( v, p, v' )
( v, p, v' )  E p
E p  X x Y.
X x Y.
Определение 18.
Тестируемые системы мы будем называть пассивными, если после подачи произвольного набора стимулов в произвольном состоянии тестируемая система за конечное время переходит в стационарное состояние.
На первый взгляд пассивные тестируемые системы составляют лишь небольшую часть всех асинхронных систем, но с точки зрения предлагаемого подхода бОльшая часть "активных" систем может быть переведена в класс пассивных. Действительно, если асинхронная система проявляет свою активность через некоторые промежутки времени, то есть периодически посылает сообщения, не инициированные внешним воздействием, то такое поведение можно моделировать как переход системы в стационарное состояние, получение ею специального стимула "время" и последующую посылку отложенных реакций. В этом случае, тестируемая система может рассматриваться как пассивная, если времени до очередной отложенной реакции достаточно, чтобы тестовая система завершила оценку корректности поведения и инициировала следующий локальный тестовый сценарий. Таким образом, класс пассивных асинхронных систем является достаточно большим и далее мы будем рассматривать тестирование только таких целевых систем.
Тестирование пассивных целевых систем, построенное по рассмотренным выше принципам, мы будем называть стационарным тестированием.
Если после завершения работы локального тестового сценария некоторые ожидаемые отложенные реакции не были получены, то состояние модели требований не будет стационарным. Таким образом, проверка стационарности состояния модели требований после завершения работы локального тестового сценария может служить решением проблемы проверки полноты набора отложенных реакций, обсуждавшийся ранее в разделе "Требования к полноте набора асинхронных реакций".
С другой стороны, непосредственная проверка стационарности не слишком удобна при наличии опциональных отложенных реакций, которые могут быть посланы тестируемой системой, а могут и отсутствовать. Для описания таких реакций разработчику теста придется вводить псевдостимул done, описывающий завершение ожидания опциональных реакций.
Чтобы упростить работу разработчика тестов, мы определим неявные трансформации асинхронной модели требований и асинхронной модели поведения, построенной по результатам работы локального сценария. При помощи данных трансформаций мы решим проблему проверки полноты набора отложенных реакций, включающего как обязательные, так и опциональные реакции.
Стабилизирующей трансформацией ST[A,VS] асинхронной модели требований A = ( V, X, Y, Z, E ) относительно множества стабильных состояний VS  V будем называть асинхронную модель требований A' = ( V', X', Y', Z', E' ), в которой:
V будем называть асинхронную модель требований A' = ( V', X', Y', Z', E' ), в которой:
- множество состояний V' = V x {T,F}, первую составляющую которого мы будем называть основной,
- множество стимулов X' = X
 {done},
{done},
- множество непосредственных реакций Y' = Y
 {ε},
{ε},
- множество отложенных реакций Z' = Z,
- множество переходов E' = { ( (v1,T), p, (v2,F) ) | ( v1, p, v2 )
 E
E 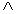 p
p  X x Y }
X x Y }
 { ( (v1,F), p, (v2,F) ) | ( v1, p, v2 )
{ ( (v1,F), p, (v2,F) ) | ( v1, p, v2 )  E }
E }
 { ( (v,F), (done,ε), (v,T) ) | v
{ ( (v,F), (done,ε), (v,T) ) | v  VS }.
VS }.
Заметим, что все состояния стабилизирующей трансформации вида (v,T) гарантированно являются стационарными, так как из них, по определению, не выходит переходов, помеченных отложенными реакциями. Семантика множества стабильных состояний заключается в том, что стабильными состояниями считаются такие состояния, в которых не ожидается ни одной обязательной отложенной реакции.
Стабилизирующей трансформацией ST[(P, )] асинхронной модели поведения ( P,
)] асинхронной модели поведения ( P,  ) будем называть асинхронную модель поведения ( P',
) будем называть асинхронную модель поведения ( P',  ' ), в которой:
' ), в которой:
- P' = P
 {(done,ε)},
{(done,ε)},
 ' =
' = 
 { ( p, (done,ε) ) | p
{ ( p, (done,ε) ) | p  P }.
P }.
Стабилизирующая трансформация модели поведения содержит дополнительное псевдовзаимодействие (done,ε), которое является максимальным элементом относительно частичного порядка  '.
'.
Стабилизирующие трансформации обоих моделей единообразно модифицируют асинхронный интерфейс целевой системы, добавляя в него псевдостимул done и непосредственную реакцию ε. Таким образом, если исходные модели были построены для общего асинхронного интерфейса ( X, Y, Z ), то их стабилизирующие трансформации будут для общего асинхронного интерфейса ( X  {done}, Y
{done}, Y  {ε}, Z ).
{ε}, Z ).
При реализации стационарного тестирования на основе асинхронного автоматного тестового сценария со сценарными функциями, в качестве локальных тестовых сценариев будут выступать автоматы-сценарные функции, а построение обхода графа сценария будет выполнять ведущий автомат. Для оценки корректности поведения целевой системы после работы локального сценария мы введем дополнительный взаимодействующий автомат, который будем называть стабилизирующим. Этот автомат будет получать сообщения о завершении очередного цикла работы автомата-сценарной функции (rx  RXi), инициировать проверку корректности поведения целевой системы и в случае ее успешного завершения вычислять новую вершину графа сценария и передавать ее ведущему автомату. В случае обнаружения некорректности поведения целевой системы стабилизирующий автомат будет посылать сообщение abort, завершая таким образом работу тестового сценария.
RXi), инициировать проверку корректности поведения целевой системы и в случае ее успешного завершения вычислять новую вершину графа сценария и передавать ее ведущему автомату. В случае обнаружения некорректности поведения целевой системы стабилизирующий автомат будет посылать сообщение abort, завершая таким образом работу тестового сценария.
Входными данными для алгоритма проверки корректности поведения являются конечная асинхронная модель поведения целевой системы ( P,  ) и асинхронная модель требований A = ( V, X, Y, Z, E ) с начальным состоянием v0
) и асинхронная модель требований A = ( V, X, Y, Z, E ) с начальным состоянием v0  V. Модель поведения содержит информацию о взаимодействиях с целевой системой в процессе работы автомата-сценарной функции и строится динамически. Модель требований задается заранее и является неизменной на протяжении всей работы тестового сценария. А вот начальное состояние модели требований изменяется в процессе тестирования и соответствует текущему состоянию целевой системы.
V. Модель поведения содержит информацию о взаимодействиях с целевой системой в процессе работы автомата-сценарной функции и строится динамически. Модель требований задается заранее и является неизменной на протяжении всей работы тестового сценария. А вот начальное состояние модели требований изменяется в процессе тестирования и соответствует текущему состоянию целевой системы.
Единственность такого состояния накладывает дополнительное ограничение на работу тестового сценария. От него требуется, чтобы все корректные линеаризации асинхронной модели поведения P завершались в одном и том же состоянии, то есть
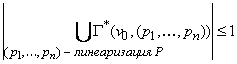
В случае выполнении данного ограничения при нахождении корректной линеаризации переменная алгоритма path[n] будет содержать всегда одно и то же состояние, которое мы будем называть конечным состоянием линеаризации. Это состояние будет выступать в качестве начального состояния модели требований для следующего цикла работы автомата-сценарной функции.
Заметим, что алгоритм проверки корректности поведения легко обобщается на случай, когда начальное состояние модели требований задано неоднозначно. То есть, когда вместо конкретного начального состояния v0 задано множество возможных начальных состояний V0. Для этого требуется только изменить инициализацию первого элемента массива path: вместо инициализации path[0] множеством, содержащим начальное состояние {v0}, использовать инициализацию множеством возможных начальных состояний V0.
Но в настоящей работе мы не будем рассматривать способы построения тестовых сценариев без данного ограничения, а оставим эту задачу в качестве направления дальнейшего развития.
Стационарный автоматный тестовый сценарий
Рассмотрим реализацию предложенного подхода более формально.
Стационарным автоматным тестовым сценарием относительно асинхронной модели требований A = ( V, X, Y, Z, E ) с множеством стабильных состояний VS  V и начальным состоянием v0
V и начальным состоянием v0  VS, называется пятерка ( SA, ASt, AIR, AHO, AGS ), где
VS, называется пятерка ( SA, ASt, AIR, AHO, AGS ), где
- SA = ( DA, Afsm, VG, XG, vg0, α,
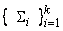 ) - асинхронный автоматный тестовый сценарий со сценарными функциями для целевой системы с асинхронным интерфейсом ( X, Y, Z ),
) - асинхронный автоматный тестовый сценарий со сценарными функциями для целевой системы с асинхронным интерфейсом ( X, Y, Z ),
- ASt = ( SSt, s0,St, XSt, YSt, ESt, QSt ) - выделенный взаимодействующий автомат, входящий в состав DA, и называемый стабилизирующим автоматом асинхронного тестового сценария DA,
- AIR
 Ã( Unit,
Ã( Unit, 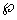 ( Ω(X,Y,Z) ) ) - асинхронная функция, замыкание которой по множеству { stop, abort } входит в состав DA,
( Ω(X,Y,Z) ) ) - асинхронная функция, замыкание которой по множеству { stop, abort } входит в состав DA,
- AHO
 Ã(
Ã( 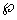 ( Ω(X,Y,Z) ) x V, Bool x V ) 8 - асинхронная функция, замыкание которой по множеству { stop, abort } входит в состав DA,
( Ω(X,Y,Z) ) x V, Bool x V ) 8 - асинхронная функция, замыкание которой по множеству { stop, abort } входит в состав DA,
- AGS
 Ã( Unit, VG ) - асинхронная функция, замыкание которой по множеству { stop, abort } входит в состав DA;
Ã( Unit, VG ) - асинхронная функция, замыкание которой по множеству { stop, abort } входит в состав DA;
и для которой выполнены следующие ограничения:
- вхождения замыканий взаимодействующих автоматов AIR, AHO и AGS и вхождения ASt, Afsm и Σi в DA различаются между собой,
- SSt = ( { s0, s1, s2, s4, s5, s6, final }
 Ω(X,Y,Z) ) x V,
Ω(X,Y,Z) ) x V,
- s0,St = ( s0, v0 ),
- XSt = { callIR, callGS, abort }
 { callHO,P,v | P
{ callHO,P,v | P  Ω(X,Y,Z), v
Ω(X,Y,Z), v  V },
V },
- YSt =
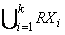
 { stop, abort }
{ stop, abort }  { resultHO,verdict,v | verdict
{ resultHO,verdict,v | verdict  Bool, v
Bool, v  V }
V }
 { resultIR,P | P
{ resultIR,P | P  Ω(X,Y,Z) },
Ω(X,Y,Z) },
где RXi = { resulti,true, resulti,false },
- ESt = { ( ( s0, v ) resulti,true?, ( s1, v ) ) | i = 1, …, k }
 { ( ( s1, v ), callIR!, ( s2, v ) ) }
{ ( ( s1, v ), callIR!, ( s2, v ) ) }
 { ( ( s2, v ), resultIR,P?, ( P, v ) ) | P
{ ( ( s2, v ), resultIR,P?, ( P, v ) ) | P  Ω(X,Y,Z) }
Ω(X,Y,Z) }
 { ( ( P, v ), callHO,P,v!, ( s4, v ) ) | P
{ ( ( P, v ), callHO,P,v!, ( s4, v ) ) | P  Ω(X,Y,Z) }
Ω(X,Y,Z) }
 { ( ( s4, v ), resultHO,true,v'?, ( s5, v' ) ) }
{ ( ( s4, v ), resultHO,true,v'?, ( s5, v' ) ) }
 { ( ( s4, v ), resultHO,false,v'?, ( s6, v ) ) }
{ ( ( s4, v ), resultHO,false,v'?, ( s6, v ) ) }
 { ( ( s5, v ), callGS!, ( s0, v ) ) }
{ ( ( s5, v ), callGS!, ( s0, v ) ) }
 { ( ( s6, v ), abort!, ( final, v ) ) }
{ ( ( s6, v ), abort!, ( final, v ) ) }
 { ( ( s0, v ), resulti,false?, ( s6, v ) ) | i = 1, …, k }
{ ( ( s0, v ), resulti,false?, ( s6, v ) ) | i = 1, …, k }
 { ( ( s0, v ), stop?, ( final, v ) ) }
{ ( ( s0, v ), stop?, ( final, v ) ) }
 { ( ( s0, v ), abort?, ( final, v ) ) }
{ ( ( s0, v ), abort?, ( final, v ) ) }
- QSt = { ( final, v ) | v
 V },
V },
- Yfsm = { resultGS,vg | vg
 VG }
VG }  { abort },
{ abort },
- асинхронная функция AIR возвращает асинхронную модель поведения, описывающую все взаимодействия с целевой системой, зафиксированные за время работы сценарной функции,
- асинхронная функция AHO получает асинхронную модель поведения P и текущее состояние модели v и возвращает true, если стабилизирующая трансформация этой модели ST[P] удовлетворяет стабилизирующей трансформации ST[A,VS] с начальным состоянием (v,T), и false - в противном случае, причем, в первом случае она также возвращает основную составляющую конечного состояния линеаризации,
- асинхронная функция AGS возвращает текущую вершину графа автомата,
- все стимулы и реакции стабилизирующего автомата являются внутренними для DA:
(XSt  YSt)
YSt) 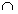 (X
(X  Y
Y  Z) = Ø,
Z) = Ø,
- всем стимулам, вызывающим асинхронные функции из стабилизирующего автомата, соответствуют единственные в рамках DA реакции, принадлежащие соответствующим асинхронным функциям,
- всем реакциям получения результата асинхронных функций из стабилизирующего автомата, соответствуют единственные в рамках DA стимулы, принадлежащие соответствующим асинхронным функциям.
Стационарный автоматный тестовый сценарий определяет правила организации стационарного тестирования на основе асинхронного автоматного тестового сценария со сценарными функциями. Основную роль здесь играет стабилизирующий автомат, который после завершения каждого цикла работы сценарной функции запрашивает модель поведения, описывающую все взаимодействия с целевой системой за время этого цикла, и проверяет корректность этой модели поведения. В случае успешной проверки стабилизирующий автомат возвращает управление управляющему автомату с указанием новой вершины в графе автомата. В противном случае тест завершается посылкой стимула abort.
Работа по оценке корректности модели поведения выполняется в асинхронной функции AHO, которая получает на вход текущее состояние модели требований и асинхронную модель поведения. К модели поведения применяется стабилизирующая трансформация и затем проверяется корректность этой трансформации относительно стабилизирующей трансформации модели требований ST[A,VS] с начальным состоянием, равным текущему состоянию модели требований. В дополнение к оценке корректности AHO возвращает основную составляющую конечного состояния линеаризации, которая становится новым текущим состоянием модели требований.
Однако, конечное состояние линеаризации может быть найдено только в том случае, когда все успешные линеаризации модели поведения ST[P] завершаются в одном и том же состоянии. Если это условие не выполняется, то асинхронная функция AHO не может выполнить свою задачу и, соответственно, стационарный автоматный тестовый сценарий не может быть применен.
Далее, мы обратимся к вопросу применимости стационарного автоматного тестового сценария и определим достаточные условия для его корректной работы.
Асинхронная модель требований A = ( V, X, Y, Z, E ) называется стационарно-детерминированной относительно множества стабильных состояний VS  V, если для любого конечного мультимножества асинхронных взаимодействий P и для любого состояния v
V, если для любого конечного мультимножества асинхронных взаимодействий P и для любого состояния v  VS
VS
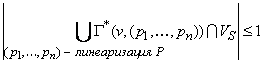
Лемма.
Если асинхронная модель требований A = ( V, X, Y, Z, E ) является стационарно-детерминированной относительно множества стабильных состояний VS  V, то произвольный стационарный автоматный тестовый сценарий относительно модели требований A с множеством стабильных состояний VS и начальным состоянием v0
V, то произвольный стационарный автоматный тестовый сценарий относительно модели требований A с множеством стабильных состояний VS и начальным состоянием v0  VS применим независимо от поведения целевой системы.
VS применим независимо от поведения целевой системы.
Доказательство.
1. Сначала мы докажем по индукции, что асинхронная функция AHO в качестве текущего состояния модели требований всегда получает стабильное состояние.
Функция AHO получает на вход состояние модели требований, которое хранится в стабилизирующем автомате сценария. В начале работы сценария это состояние инициализируется начальным состоянием v0, которое является стабильным по определению (v0  VS).
VS).
В дальнейшем, это состояние может измениться только в переходе ( ( s4, v ), resultHO,true,v'?, ( s5, v' ) ), при получении результата от асинхронной функции AHO, так как согласно четырнадцатому ограничению стационарного автоматного тестового сценария реакции получения результата асинхронной функции AHO из стабилизирующего автомата resultHO,true,v' соответствует единственный в рамках DA стимул, принадлежащий соответствующей асинхронной функции. При этом новое состояние совпадает с конечным состоянием линеаризации, которое возвращается функцией AHO.
В качестве индуктивного перехода покажем, что для любой асинхронной модели поведения P, если стабилизирующая трансформация этой модели ST[P] удовлетворяет стабилизирующей трансформации ST[A,VS] с начальным состоянием (v,T), где v стабильно (v  VS), и конечное состояние линеаризации (v',x') существует, то оно также является стабильным (v'
VS), и конечное состояние линеаризации (v',x') существует, то оно также является стабильным (v'  VS).
VS).
Действительно, по определению, { (v',x') } = Г* ( (v,T), ( p1, p2, …, pn ) ) для некоторой линеаризации ( p1, p2, …, pn ) модели поведения ST[P]. Так как псевдовзаимодействие (done,ε) является максимальным элементом в стабилизирующей трансформации ST[P], то pn = (done,ε). С другой стороны, по определению стабилизирующей трансформации ST[A,VS], все переходы, помеченные (done,ε), могут быть только вида ( (w,F), (done,ε), (w,T) ), где w  VS. Следовательно
VS. Следовательно
 W
W  V x {T,F} ( W, pn )
V x {T,F} ( W, pn )  VS x {T},
VS x {T},
и
{ (v',x') } = Г* ( (v,T), ( p1, p2, …, pn ) ) = Г( … Г( {(v,T)}, p1 ), … pn )  VS x {T}.
VS x {T}.
То есть v'  VS, что и требовалось доказать.
VS, что и требовалось доказать.
2. В качестве завершающего шага мы докажем, что для любой асинхронной модели поведения P, если стабилизирующая трансформация этой модели ST[P] удовлетворяет стабилизирующей трансформации ST[A,VS] с начальным состоянием (v,T), где v стабильно (v  VS), то конечное состояние линеаризации (v',x') существует. Из этого следует, что асинхронная функция AHO всегда может выполнить свою задачу, так как согласно первому пункту она всегда получает на вход только стабильные состояния модели требований.
VS), то конечное состояние линеаризации (v',x') существует. Из этого следует, что асинхронная функция AHO всегда может выполнить свою задачу, так как согласно первому пункту она всегда получает на вход только стабильные состояния модели требований.
Предположим, что это не так. То есть существует асинхронная модель поведения P, стабильное состояние модели требований v  VS и два состояния (v',x') и (v'',x'') такие, что
VS и два состояния (v',x') и (v'',x'') такие, что
{ (v',x'), (v'',x'') } 
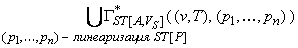 и (v',x') ≠ (v'',x'').
и (v',x') ≠ (v'',x'').
Тогда существует две линеаризации модели поведения ST[P] ( p1,1, p1,2, …, p1,n ) и ( p2,1, p2,2, …, p2,n ) такие, что
(v', x') 
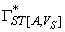 ( (v,T), ( p1,1, p1,2, …, p1,n ) ) и
( (v,T), ( p1,1, p1,2, …, p1,n ) ) и
(v'',x'') 
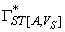 ( (v,T), ( p2,1, p2,2, …, p2,n ) ).
( (v,T), ( p2,1, p2,2, …, p2,n ) ).
Повторяя рассуждения из первого пункта, можно показать, что x' = x'' = T, p1,n = p2,n = (done,ε), v'  VS, v''
VS, v''  VS и
VS и
(v', F) 
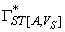 ( (v,T), ( p1,1, p1,2, …, p1,n-1 ) ) и
( (v,T), ( p1,1, p1,2, …, p1,n-1 ) ) и
(v'',F) 
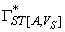 ( (v,T), ( p2,1, p2,2, …, p2,n-1 ) ).
( (v,T), ( p2,1, p2,2, …, p2,n-1 ) ).
То есть в асинхронной модели требований ST[A,VS] существует путь, начинающийся в (v,T), помеченный ( p1,1, p1,2, …, p1,n-1 ) и заканчивающийся в (v', F):
(v,T)  (v2,x2)
(v2,x2)  …
…  (v', F).
(v', F).
Так как { p1,1, p1,2, …, p1,n-1 }  ( (X x Y)
( (X x Y)  Z ), то из определения ST[A,VS] следует, что в исходной модели требований A существует путь
Z ), то из определения ST[A,VS] следует, что в исходной модели требований A существует путь
v  v2
v2  …
… 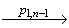 v'.
v'.
Следовательно, v' 
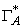 ( v, ( p1,1, p1,2, …, p1,n-1 ) ).
( v, ( p1,1, p1,2, …, p1,n-1 ) ).
Аналогично, v'' 
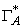 ( v, ( p2,1, p2,2, …, p2,n-1 ) ).
( v, ( p2,1, p2,2, …, p2,n-1 ) ).
И так как мультимножества взаимодействий { p1,1, p1,2, …, p1,n-1 } и { p2,1, p2,2, …, p2,n-1 } совпадают, то существует мультимножество взаимодействий P* = { p1,1, p1,2, …, p1,n 1 }:
{ v', v'' } 
 , причем v' ≠ v'' и v'
, причем v' ≠ v'' и v'  VS, v''
VS, v''  VS.
VS.
То есть 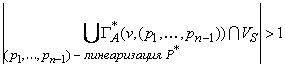
и асинхронная модель требований A = ( V, X, Y, Z, E ) не является стационарно-детерминированной относительно множества стабильных состояний VS  V.
V.
Следовательно, наше предположение не верно и v' = v'', что и требовалось доказать.
Таким образом, стационарные автоматные тестовые сценарии могут применяться для тестирования относительно стационарно-детерминированных моделей требований, которые представляют широкий класс моделей требований. С другой стороны, требование стационарной-детерминированности не является необходимым, и стационарные автоматные тестовые сценарии могут работать с другими моделями при условии, что в процессе тестирования не встретится ситуация с отсутствием конечного состояния линеаризации по причине наличия нескольких успешных линеаризаций, заканчивающихся в различных состояниях.
Асинхронная функция AHO может быть реализована в предположении, что модель требований является стационарно-детерминированной. В этом случае она может возвращать в качестве конечного состояния постсостояние первой успешной линеаризации. Также возможна реализация функция AHO, которая будет верифицировать корректность модели требований, находя все успешные линеаризации и проверяя, что все их постсостояния совпадают.
Последовательной композицией набора асинхронных моделей поведения 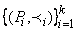 мы будем называть асинхронную модель поведения ( P,
мы будем называть асинхронную модель поведения ( P,  ), в которой мультимножество P получено объединением элементов мультимножеств Pi (P =
), в которой мультимножество P получено объединением элементов мультимножеств Pi (P = 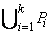 ), а частичный порядок
), а частичный порядок  составлен из частичных порядков
составлен из частичных порядков  i:
i:
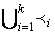
 { ( p1, p2 ) | p1
{ ( p1, p2 ) | p1  Pi
Pi 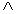 p2
p2  Pj
Pj 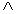 i < j }.
i < j }.
Последовательная композиция моделей поведения представляет собой объединенную модель поведения, в которой присутствуют все взаимодействия из этих моделей поведения, причем считается, что любое взаимодействие из i-ой модели поведения происходило позже всех взаимодействий, принадлежащих предыдущим моделям.
Лемма.
Предположим, что модель требований A = ( V, X, Y, Z, E ) является стационарно-детерминированной относительно множества стабильных состояний VS  V. Предположим также, что в процессе работы стационарного автоматного тестового сценария ( SA, ASt, AIR, AHO, AGS ) относительно модели требований A с множеством стабильных состояний VS и начальным состоянием v0
V. Предположим также, что в процессе работы стационарного автоматного тестового сценария ( SA, ASt, AIR, AHO, AGS ) относительно модели требований A с множеством стабильных состояний VS и начальным состоянием v0  VS асинхронная функция AIR последовательно возвращала стабилизирующему автомату асинхронные модели поведения
VS асинхронная функция AIR последовательно возвращала стабилизирующему автомату асинхронные модели поведения 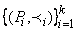 . Тогда, все вердикты функции AHO, посланные стабилизирующему автомату, были положительными, в том, и только в том случае, когда последовательная композиция стабилизирующих трансформаций моделей поведения
. Тогда, все вердикты функции AHO, посланные стабилизирующему автомату, были положительными, в том, и только в том случае, когда последовательная композиция стабилизирующих трансформаций моделей поведения 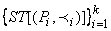 удовлетворяет стабилизирующей трансформации модели требований ST[A] с начальным состоянием v0.
удовлетворяет стабилизирующей трансформации модели требований ST[A] с начальным состоянием v0.
Доказательство.
1. Докажем утверждение леммы в прямую сторону. Предположим, что все вердикты функции AHO, посланные стабилизирующему автомату, были положительными, и покажем, что последовательная композиция 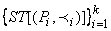 удовлетворяет ST[A] с начальным состоянием v0.
удовлетворяет ST[A] с начальным состоянием v0.
В пункте 2 предыдущей леммы мы показали, что если асинхронная функция AHO получает на вход асинхронную модель поведения Pi и состояние модели требований v и возвращает положительный вердикт и конечное состояние линеаризации v', то в модели требований ST[A] существует путь (v,T) 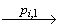 …
… 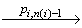 (v',F)
(v',F) 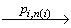 (v',T) для некоторой линеаризации ( pi,1, pi,2, …, pi,n(i)-1, pi,n(i) ) модели ST[Pi] и pi,n (i) = done.
(v',T) для некоторой линеаризации ( pi,1, pi,2, …, pi,n(i)-1, pi,n(i) ) модели ST[Pi] и pi,n (i) = done.
Как мы уже отмечали, функция AHO получает на вход состояние модели требований, которое хранится в стабилизирующем автомате сценария. Это состояние инициализируется в начале работы сценария начальным состоянием v0, а в дальнейшем оно изменяется только в переходах вида ( ( s4, v ), resultHO,true,v'?, ( s5, v' ) ). Эти переходы осуществляются при получении результата от асинхронной функции AHO, так как согласно четырнадцатому ограничению стационарного автоматного тестового сценария каждой реакции получения результата асинхронной функции AHO из стабилизирующего автомата resultHO,true,v' соответствует единственный в рамках DA стимул, принадлежащий соответствующей асинхронной функции.
Отсюда следует, что в модели требований ST[A] существует путь
(v0,T)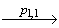 …
… 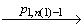 (v'1,F)
(v'1,F) 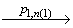 (v'1,T)
(v'1,T)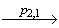 …
… 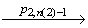 (v'2,F)
(v'2,F) 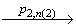 (v'2,T) …
(v'2,T) …
… (v'k-1,T) 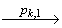 …
… 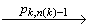 (v'k,F)
(v'k,F) 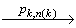 (v'k,T).
(v'k,T).
Покажем, что последовательность
( p1,1, …, p1,n(1)-1, p1,n(1), p2,1, …, p2,n(2)-1, p2,n(2), …, pk,1, …, pk,n(k)-1, pk,n(k) )
является линеаризацией ( P,  ), где ( P,
), где ( P,  ) обозначается последовательная композиция
) обозначается последовательная композиция 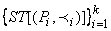 .
.
Действительно, все элементы мультимножества P присутствуют в этой последовательности, а порядок элементов последовательности не противоречит частичному порядку  .
.
Предположим, что последнее утверждение не верно. Тогда в последовательности существуют два таких элемента pi,r и pj,s, что pj,s  pi,r, но pi,r расположен раньше, чем pj,s, то есть (i < j)
pi,r, но pi,r расположен раньше, чем pj,s, то есть (i < j) 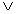 (i = j)
(i = j) 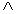 (r < s).
(r < s).
В первом случае, если i < j, то pi,r  pj,s, согласно определению частичного порядка
pj,s, согласно определению частичного порядка  , и следовательно ¬ pj,s
, и следовательно ¬ pj,s  pi,r.
pi,r.
Во втором случае, если i = j и r < s, то из pj,s  pi,r следует, что pj,s
pi,r следует, что pj,s  i pi,r. Но тогда ( pi,1, pi,2, …, pi,n(i) ) не может быть линеаризацией модели ST[Pi], так как порядок элементов pj,s и pi,r противоречит частичному порядку ST[
i pi,r. Но тогда ( pi,1, pi,2, …, pi,n(i) ) не может быть линеаризацией модели ST[Pi], так как порядок элементов pj,s и pi,r противоречит частичному порядку ST[ i]. Следовательно, наше предположение не верно и порядок элементов последовательности не противоречит частичному порядку
i]. Следовательно, наше предположение не верно и порядок элементов последовательности не противоречит частичному порядку  .
.
Таким образом, рассматриваемая последовательность является линеаризацией последовательной композиции 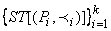 , а из существования пути
, а из существования пути
(v0,T)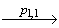 …
… 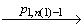 (v'1,F)
(v'1,F) 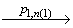 (v'1,T)
(v'1,T)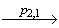 …
… 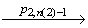 (v'2,F)
(v'2,F) 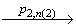 (v'2,T) …
(v'2,T) …
… (v'k-1,T) 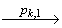 …
… 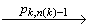 (v'k,F)
(v'k,F) 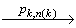 (v'k,T).
(v'k,T).
в автомате A следует, что последовательная композиция 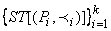 удовлетворяет модели требований A с начальным состоянием v0.
удовлетворяет модели требований A с начальным состоянием v0.
2. Докажем утверждение леммы в обратную сторону. Предположим, что первые k-1 вердикта функции AHO, посланные стабилизирующему автомату, были положительными, а k-й вердикт - отрицательный. Покажем, что в этом случае последовательная композиция 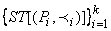 не удовлетворяет ST[A] с начальным состоянием v0.
не удовлетворяет ST[A] с начальным состоянием v0.
Предположим, что это не так и последовательная композиция 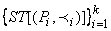 удовлетворяет ST[A] с начальным состоянием v0. То есть в модели требований ST[A] существует путь
удовлетворяет ST[A] с начальным состоянием v0. То есть в модели требований ST[A] существует путь
(v0,T) 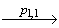 …
… 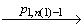 (v1,n (1)-1, x1,n(1)-1)
(v1,n (1)-1, x1,n(1)-1) 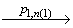 (v1,n(1) , x1,n(1) )
(v1,n(1) , x1,n(1) ) 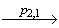 …
…
… (vk-1,n(k-1) , xk-1,n(k-1) ) 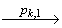 …
… 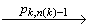 (vk,n(k)-1, x k,n(k)-1)
(vk,n(k)-1, x k,n(k)-1) 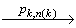 (vk,n(k) , x k,n(k) ),
(vk,n(k) , x k,n(k) ),
где ( p1,1, …, p1,n(1)-1, p1,n(1) , p2,1, …, p2,n(2)-1, p2,n(2) , …, pk,1, …, pk,n(k)-1, pk,n(k) ) - некоторая линеаризацией последовательной композиции 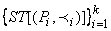 . Согласно определению стабилизирующей трансформации максимальным элементом в SP[ (Pi,
. Согласно определению стабилизирующей трансформации максимальным элементом в SP[ (Pi, i) ] является псевдовзаимодействие (done,ε). Следовательно
i) ] является псевдовзаимодействие (done,ε). Следовательно  i
i  {1,…,k} pi,n(i) = (done,ε).
{1,…,k} pi,n(i) = (done,ε).
По определению стабилизирующей трансформации модели требований ST[A] все переходы, помеченные (done,ε), имеют вид ( (w,F), (done,ε), (w,T) ), где w  VS. То есть
VS. То есть
 i
i  {1,…,k} (vi,n(1)-1, xi,n(i)-1)
{1,…,k} (vi,n(1)-1, xi,n(i)-1)  (vi,n(i) , xi,n(i) ) ≡ (v'i,F)
(vi,n(i) , xi,n(i) ) ≡ (v'i,F)  (v'i,T),
(v'i,T),
где v'i  VS.
VS.
Докажем по индукции, что  i
i  {1, …, k-1} в результате i-го вызова функции AHO из стабилизирующего автомата, та возвращает состояние модели требований равное v'i.
{1, …, k-1} в результате i-го вызова функции AHO из стабилизирующего автомата, та возвращает состояние модели требований равное v'i.
База индукции . Согласно определению стабилизирующего автомата функция AHO в первый раз получает модель поведения (P1, 1) и состояние v0
1) и состояние v0  VS. Если k > 1, то функция возвращает положительный вердикт и основную составляющую конечного состояния линеаризации ( v', x' ). Так как модель требований A является стационарно-детерминированной, то конечное состояние линеаризации существует, причем v' = v'1, так как (v0,T)
VS. Если k > 1, то функция возвращает положительный вердикт и основную составляющую конечного состояния линеаризации ( v', x' ). Так как модель требований A является стационарно-детерминированной, то конечное состояние линеаризации существует, причем v' = v'1, так как (v0,T)  …
…  (v'1,F)
(v'1,F)  (v'1,T) является успешной линеаризацией модели (P1,
(v'1,T) является успешной линеаризацией модели (P1, 1).
1).
Предположение индукции . Предположим, что после i-го вызова функции AHO из стабилизирующего автомата, та возвращает состояние модели требований v'i.
Шаг индукции . Докажем, что если после i+1-го вызова функция AHO возвращает положительный вердикт и состояние модели требований w, то w = v'i+1.
По определению стабилизирующего автомата при i+1-ом вызове функция AHO получает модель поведения (Pi+1, i+1) и состояние v'i
i+1) и состояние v'i  VS. Если i+1 < k, то по условиям леммы функция возвращает положительный вердикт и основную составляющую конечного состояния линеаризации w. Заметим, что в автомате ST[A] существует путь (v'i,T)
VS. Если i+1 < k, то по условиям леммы функция возвращает положительный вердикт и основную составляющую конечного состояния линеаризации w. Заметим, что в автомате ST[A] существует путь (v'i,T) 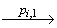 …
…  (v'i+1,F)
(v'i+1,F) 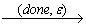 (v'i+1,T), который является одной из успешных линеаризаций модели (Pi+1,
(v'i+1,T), который является одной из успешных линеаризаций модели (Pi+1, i+1). Следовательно, состояние w совпадает с состоянием v'i+1.
i+1). Следовательно, состояние w совпадает с состоянием v'i+1.
Рассмотрим работу функции AHO при k-ом вызове. Стабилизирующий автомат передает ей модель поведения (Pk, k) и состояние w
k) и состояние w  V, полученное от функции AHO на предыдущем вызове, если k > 1, или v0
V, полученное от функции AHO на предыдущем вызове, если k > 1, или v0  V, если k = 1. В первом случае, как мы показали по индукции, состояние модели требований w равно v'k-1.
V, если k = 1. В первом случае, как мы показали по индукции, состояние модели требований w равно v'k-1.
Исходя из предположения второго пункта леммы, существует линеаризация модели поведения SP[ (Pk, k) ] ( pk,1, …, pk,n(k)-1, pk,n(k) ), такая что в автомате ST[A] существует путь (v'k-1,T)
k) ] ( pk,1, …, pk,n(k)-1, pk,n(k) ), такая что в автомате ST[A] существует путь (v'k-1,T) 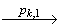 …
… 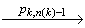 (v'k,F)
(v'k,F)  (v'k,T). И так как модель требований A является стационарно-детерминированной, то согласно предыдущей лемме конечное состояние линеаризации существует и совпадает с (v'k,T). Следовательно, функция AHO, по определению, должна вернуть положительный вердикт и состояние v'k. Но эта функция вернула на k-ом шаге отрицательный вердикт, то есть наше предположение не верно, и последовательная композиция
(v'k,T). И так как модель требований A является стационарно-детерминированной, то согласно предыдущей лемме конечное состояние линеаризации существует и совпадает с (v'k,T). Следовательно, функция AHO, по определению, должна вернуть положительный вердикт и состояние v'k. Но эта функция вернула на k-ом шаге отрицательный вердикт, то есть наше предположение не верно, и последовательная композиция 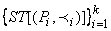 не удовлетворяет модели требований ST[A] с начальным состоянием v0.
не удовлетворяет модели требований ST[A] с начальным состоянием v0.
Из данной леммы можно сделать вывод, что стационарный автоматный тестовый сценарий, проверяя корректность небольших моделей поведения, описывающих только часть поведения целевой системы в процессе тестирования, в итоге проверяет корректность поведения целевой системы в процессе всего тестирования в целом. Таким образом, декомпозиция задачи оценки корректности осуществлена корректным образом.
Асинхронный тестовый сценарий dfsm
Основным механизмом построения тестовых сценариев в синхронном случае является механизм построения тестового сценария dfsm. Этот механизм основан на неизбыточном алгоритме обхода на классе детерминированных сильно-связных конечных ориентированных графов αdfsm[26]. Для стационарного тестирования асинхронных систем данный алгоритм обхода также будет выступать в качестве одного из основных.
Определение 19.
Асинхронным тестовым сценарием dfsm относительно асинхронной модели требований A ( V, X, Y, Z, E ) с множеством стабильных состояний VS  V и начальным состоянием v0
V и начальным состоянием v0  VS, называется стационарный автоматный тестовый сценарий, в котором в качестве алгоритма движения по графу сценария используется алгоритм обхода αdfsm.
VS, называется стационарный автоматный тестовый сценарий, в котором в качестве алгоритма движения по графу сценария используется алгоритм обхода αdfsm.
Любое конечное функционирование алгоритма обхода αdfsm приводит
- либо к обнаружению нарушения требований детерминированности или сильно-связности графа сценария,
- либо к построению обхода этого графа.
Таким образом, если граф сценария при любом корректном функционировании целевой системы является детерминированным и сильно-связным, то в результате успешной работы асинхронного тестового сценария dfsm путь, пройденный по графу сценария, является обходом этого графа. В этом случае, в каждом достижимом состоянии графа сценария будет вызвана каждая допустимая в данном состоянии асинхронная сценарная функция. Это позволяет строить асинхронные тестовые сценарии на основе так называемой автоматной композиции, которая продемонстрировала свои достоинства в ходе применения технологии UniTesK для тестирования синхронных систем различного рода.
Однако, при тестировании асинхронных систем недетерминированное поведение встречается значительно чаще, так как в случае параллельных взаимодействий результат может определяться последовательностью внутренних событий целевой системы, не поддающихся наблюдению и тем более управлению со стороны тестовой системы. Поэтому потребность в использовании алгоритмов обхода, способных работать с недетерминированными графами, для асинхронных тестовых сценариев выше, чем в синхронном случае. Один из таких алгоритмов, мы рассмотрим в следующем разделе.
Алгоритм обхода ndfsm
Основная идея алгоритма обхода ndfsm заключается в следующем. Если в недетерминированном графе существует детерминированный сильносвязный полный остовный подграф, то алгоритм движения может использовать этот подграф для построения обхода, не сталкиваясь непосредственно с проблемами недетерминизма.
Ориентированный граф G' = ( VG', XG', EG' ) называется остовным подграфом ориентированного графа G = ( VG, XG, EG ), если VG' = VG, XG' = XG и EG'  EG.
EG.
Остовный подграф G' = ( VG', XG', EG' ) ориентированного графа G = ( VG, XG, EG ) называется полным остовным подграфом, если
 ( v, xg, v' )
( v, xg, v' )  EG ( v, xg, v'' )
EG ( v, xg, v'' )  EG ( v, xg, v' )
EG ( v, xg, v' )  EG'
EG'  ( v, xg, v'' )
( v, xg, v'' )  EG'.
EG'.
Напомним, что алгоритмом движения на ориентированных графах называется функция α, которая по ориентированному графу G = ( VG, XG, EG ), текущей вершине v  VG и пройденному маршруту ( e1, e2, …, en ) определяет следующее действие a
VG и пройденному маршруту ( e1, e2, …, en ) определяет следующее действие a  XG
XG  { τ }.
{ τ }.
Пусть e = ( e1, e2, …, en ) - пройденный маршрут в графе G = ( VG, XG, EG ). Тогда мы будем использовать следующие обозначения. Множеством пройденных вершин VGe мы будем называть множество вершин пройденного маршрута:
VGe = { vg  VG |
VG |  ei: ei = ( vi, xgi, v'i )
ei: ei = ( vi, xgi, v'i )  (vi = vg
(vi = vg  v'i = vg) }
v'i = vg) }
Пройденным подграфом мы будем называть граф G'e = ( VGe, XG, { e1, e2, …, en } ).
Пусть ei = ( vi, xgi, v'i ). Тогда детерминированным пройденным подграфом мы будем называть граф G''e = ( VGe, XG, { ei |  j
j  { 1, … , n } (vi ≠ vj
{ 1, … , n } (vi ≠ vj  xgi ≠ xgj
xgi ≠ xgj  v'i = v'j) } ).
v'i = v'j) } ).
Будем говорить, что стимул xg пройден в вершине vg, если существуют такая вершина vg'  VG и дуга ei
VG и дуга ei  e, что ei = ( vg, xg, vg' ).
e, что ei = ( vg, xg, vg' ).
Если в вершине vg все допустимые стимулы являются пройденными, то такая вершина будет называться завершенной.
Для обеспечения детерминированности функции мы будем считать, что множество стимулов XG является фундированным, то есть множество линейно упорядоченно и в нем отсутствует бесконечно убывающая последовательность элементов.
Определение 20.
Алгоритмом движения ndfsm мы будем называть функцию αndfsm, которая по неизбыточному описанию ориентированного графа G = ( VG, XG, π ), текущей вершине v  VG и пройденному маршруту e = ( e1, e2, …, en ) вычисляет действие a
VG и пройденному маршруту e = ( e1, e2, …, en ) вычисляет действие a  XG
XG  { τ } следующим образом:
{ τ } следующим образом:
- Если текущая вершина не является завершенной, то функция возвращает минимальный стимул из π(v), который не является пройденным в текущей вершине;
- Иначе, если в детерминированном пройденном подграфе существует маршрут, ведущий из текущей вершины в какую-либо из незавершенных пройденных вершин, то функция возвращает стимул, приписанный к дуге ei пройденного маршрута, которая обладает минимальным индексом среди всех дуг, являющихся первыми дугами в кратчайших маршрутах детерминированного пройденного подграфа, ведущих из текущей вершины в какую-либо из незавершенных пройденных вершин;
- В противном случае функция возвращает τ.
Корректность определения следует из фундированности множества стимулов и конечности пройденного подграфа.
При работе с недетерминированными графами алгоритм движения не может гарантировать обход всех дуг графа, так как алгоритм не может выбрать конкретную дугу среди набора дуг, начинающихся в одной вершине и помеченных одним стимулом. Этот выбор происходит недетерминированно и независимо от работы алгоритма движения. Поэтому для недетерминированных графов вводится понятие обхода по стимулам, которое совпадает с понятием обхода на классе детерминированных графов и является более слабым на классе недетерминированных графов.
Обходом по стимулам [27] конечного ориентированного графа G = ( VG, XG, EG ) называется маршрут v1  v2
v2  …
…  vn, в котором для каждой дуги ( v, x, v' )
vn, в котором для каждой дуги ( v, x, v' )  EG существует i
EG существует i  { 1, … , n-1 }, такое что v = vi и x = xi.
{ 1, … , n-1 }, такое что v = vi и x = xi.
Алгоритм движения α называется алгоритмом обхода по стимулам на классе конечных ориентированных графов Æ, если на любом графе G из класса Æ любое функционирование алгоритма движения α является конечным обходом по стимулам графа G.
Лемма.
Алгоритм движения ndfsm является алгоритмом обхода по стимулам на классе конечных графов, обладающих детерминированным сильносвязным полным остовным подграфом.
Доказательство.
Предположим, что это не так. Тогда существует конечный граф G = ( VG, XG, EG ), обладающий детерминированным сильносвязным полным остовным подграфом, и функционирование e = ( e1, e2, …, en, … ) алгоритма ndfsm на этом графе такие, что e не является конечным обходом по стимулам графа G. Такое может быть в двух случаях: если функционирование e является конечным, но не является обходом по стимулам графа G, и если функционирование e является бесконечным.
1. Предположим, что функционирование e = ( e1, e2, …, en ) является конечным, но не является обходом по стимулам графа G. Тогда из определения функционирования следует, что αndfsm( A, v'n, e ) = τ 9. Следовательно вершина v'n является завершенной и в детерминированном пройденном подграфе G''e не существует маршрута, ведущего из вершины v'n в какую-либо из незавершенных пройденных вершин.
С другой стороны e не является обходом по стимулам графа G, то есть в графе G существует такая дуга ( v, x, v' )  EG, что не существует такого i
EG, что не существует такого i  { 1, … , n }, что v = vi и x = xi.
{ 1, … , n }, что v = vi и x = xi.
Рассмотрим детерминированный сильносвязный полный остовный подграф G' = ( VG', XG', EG' ) графа G. Так как подграф является остовным, то обе вершины v и v'n принадлежат VG'. Так как граф G конечный, а его подграф G' - сильносвязный, то существует конечный маршрут f = ( f1, f2, …, fk ), ведущий из v'n в v. Пусть fi = ( wi, yi, w'i ). Тогда для всех i  { 1, … , k } из вершины wi в графе G выходит одна единственная дуга fi, помеченная стимулом yi. Предположим, что существует вторая такая дуга: ( wi, yi, w''i )
{ 1, … , k } из вершины wi в графе G выходит одна единственная дуга fi, помеченная стимулом yi. Предположим, что существует вторая такая дуга: ( wi, yi, w''i )  EG. Тогда эта дуга также принадлежит и подграфу G' ( ( wi, yi, w''i )
EG. Тогда эта дуга также принадлежит и подграфу G' ( ( wi, yi, w''i )  EG' ), так как подграф G' является полным остовным подграфом. А это противоречит тому, что подграф G' является детерминированным. Следовательно, наше предположение относительно существования второй дуги ( wi, yi, w''i )
EG' ), так как подграф G' является полным остовным подграфом. А это противоречит тому, что подграф G' является детерминированным. Следовательно, наше предположение относительно существования второй дуги ( wi, yi, w''i )  EG неверно и дуга ( wi, yi, w'i ) является единственной дугой в графе G, выходящей из wi и помеченной стимулом yi.
EG неверно и дуга ( wi, yi, w'i ) является единственной дугой в графе G, выходящей из wi и помеченной стимулом yi.
Докажем индукцией по пути f = ( f1, f2, …, fk ), что все вершины w'i являются завершенными для i  { 1, … , k }.
{ 1, … , k }.
База индукции . Вершина w1 = v'n  VGe является завершенной, по определению функционирования и функции αndfsm.
VGe является завершенной, по определению функционирования и функции αndfsm.
Предположение индукции . Пусть вершина w'i-1 = wi является завершенной.
Шаг индукции . Так как вершина wi является завершенной, стимул yi является допустимым в этой вершине и дуга ( wi, yi, w'i ) является единственной дугой, выходящей из wi и помеченной стимулом yi, то дуга ( wi, yi, w'i ) также является пройденной, то есть ( wi, yi, w'i )  e. Отсюда следует, что дуга ( wi, yi, w'i ) принадлежит детерминированному пройденному подграфу G''e, так как эта дуга является пройденной и детерминированной. На этом основании можно сделать вывод, что вершина w'i является завершенной, так как в противном случае мы нашли маршрут ( f1, f2, …, fi ) в детерминированном пройденном подграфе G''e, ведущий из v'n в одну из незавершенных пройденных вершин.
e. Отсюда следует, что дуга ( wi, yi, w'i ) принадлежит детерминированному пройденному подграфу G''e, так как эта дуга является пройденной и детерминированной. На этом основании можно сделать вывод, что вершина w'i является завершенной, так как в противном случае мы нашли маршрут ( f1, f2, …, fi ) в детерминированном пройденном подграфе G''e, ведущий из v'n в одну из незавершенных пройденных вершин.
Мы доказали, что все вершины w'i являются завершенными. Следовательно, и вершина w'k = v  VGe также является завершенной, что противоречит нашему предположению о том, что e не является обходом по стимулам графа G. Следовательно, это предположение не верно и функционирование e не является конечным.
VGe также является завершенной, что противоречит нашему предположению о том, что e не является обходом по стимулам графа G. Следовательно, это предположение не верно и функционирование e не является конечным.
2. Предположим, что функционирование e = ( e1, e2, …, en, … ) является бесконечным. Тогда для всех i ≥ 0 αndfsm( A, v'i, ( e1, …, ei ) ) ≠ τ.
Определим функцию βG на графе G, устанавливающую соответствие между маршрутом ( e1, …, ei ) в графе G и парой натуральных чисел (b1,b2), следующим образом:
- b1 равно числу дуг графа G, отсутствующих в маршруте ( e1, …, ei ), |EG \ { e1, …, ei }|;
- b2 равно
- 0, если i = 0, вершина v'i является незавершенной или в детерминированном пройденном подграфе нет маршрута, ведущего из вершины v'i и в какую-либо из незавершенных пройденных вершин;
- минимальной длине маршрута в детерминированном пройденном подграфе, начинающегося в вершине v'i и заканчивающегося в какой-либо из незавершенных пройденных вершин, в противном случае.
Определим на множестве пар натуральных чисел линейный порядок:
(b1,b2) < (b'1,b'2)  b1 < b'1
b1 < b'1  (b1 = b'1
(b1 = b'1  b2 < b'2)
b2 < b'2)
Отметим, что множество пар натуральных чисел с данным линейным порядком образуют фундированное множество, то есть множество, в котором отсутствует бесконечно убывающая последовательность элементов.
Согласно определению βG( () ) = (|EG|,0).
Покажем, что для любого префикса ( e1, …, ei ) функционирования e
βG( ( e1, …, ei, ei+1 ) ) < βG( ( e1, …, ei ) )
Для всех i ≥ 0 αndfsm( A, v'i, ( e1, …, ei ) ) ≠ τ. Следовательно, либо вершина v'i не является завершенной, либо в детерминированном пройденном подграфе существует маршрут, ведущий из вершины v'i в какую-либо из незавершенных пройденных вершин.
Рассмотрим первый случай. Если вершина v'i не является завершенной, то αndfsm возвращает минимальный стимул из π(v), который не является пройденным в вершине v'i. На этом основании можно сделать вывод, что ei+1 является дугой, не принадлежащей { e1, …, ei }. Поэтому первый компонент βG( ( e1, …, ei+1 ) ) на единицу меньше первого компонента βG( ( e1, …, ei ) ), откуда следует, что βG( ( e1, …, ei, ei+1 ) ) < βG( ( e1, …, ei ) ).
Рассмотрим второй случай. Если вершина v'i является завершенной и в детерминированном пройденном подграфе существует маршрут, ведущий из вершины v'i в какую-либо из незавершенных пройденных вершин, то αndfsm возвращает стимул, приписанный к дуге ej пройденного маршрута, которая обладает минимальным индексом среди всех дуг, являющихся первыми дугами в кратчайших маршрутах детерминированного пройденного подграфа, ведущих из текущей вершины в какую-либо из незавершенных пройденных вершин. При этом дуга ei+1 может либо совпасть c дугой ej, либо нет.
Если дуга ei+1 совпадает c дугой ej, то уменьшается на единицу второй компонент функции βG, так как кратчайший маршрут в детерминированном пройденном подграфе станет на одну дугу короче, или же в результате перехода будет достигнута незавершенная вершина. При этом первая компонента функции βG останется неизменной, поэтому βG( ( e1, …, ei, ei+1 ) ) будет меньше βG( ( e1, …, ei ) ).
Если дуга ei+1 не совпадает c дугой ej, то эта дуга не принадлежит { e1, …, ei }, так как в противном случае дуга ej не была бы частью детерминированного пройденного подграфа. Следовательно первый компонент βG( ( e1, …, ei+1 ) ) на единицу меньше первого компонента βG( ( e1, …, ei ) ), то есть βG( ( e1, …, ei, ei+1 ) ) < βG( ( e1, …, ei ) ).
Мы показали, что для всех i ≥ 0 βG( ( e1, …, ei, ei+1 ) ) < βG( ( e1, …, ei ) ). Следовательно функционирование e не может быть бесконечным, так как в противном случае последовательность βG( ( e1, …, ei ) ) образует бесконечно убывающую подпоследовательность в фундированном множестве.
Алгоритм движения ndfsm позволяет заменять стандартный алгоритм dfsm, в тех случаях когда отдельные сценарные функции имеют недетерминированную природу, а другие гарантировано обеспечивают детерминированное движение по графу.
Определение 21.
Асинхронным тестовым сценарием ndfsm относительно асинхронной модели требований A = ( V, X, Y, Z, E ) с множеством стабильных состояний VS  V и начальным состоянием v0
V и начальным состоянием v0  VS, называется стационарный автоматный тестовый сценарий, в котором в качестве алгоритма движения по графу сценария используется алгоритм обхода αndfsm.
VS, называется стационарный автоматный тестовый сценарий, в котором в качестве алгоритма движения по графу сценария используется алгоритм обхода αndfsm.
Параллельные воздействия на целевую систему
Асинхронные тестовые сценарии, рассмотренные ранее, не предоставляют разработчику тестов никакой автоматизации в осуществлении параллельных тестовых воздействий на целевую систему. Чтобы выполнять параллельные тестовые воздействия в стационарных автоматных тестовых сценариях необходимо вручную описывать правила их осуществления.
В данном разделе мы рассмотрим возможные варианты осуществления параллельных тестовых воздействий в автоматизированном режиме. В качестве таких вариантов были выделены следующие возможности:
- параллельная работа независимых тестовых сценариев;
- параллельное выполнение сценарных функций в рамках работы одного тестового сценария;
- организация параллельных воздействий на уровне сценарных функций.
Наиболее высокий уровень на котором можно организовать параллелизм - это уровень тестовых сценариев. Несколько тестовых сценариев можно запустить независимо друг от друга при условии, что каждый из них будет работать со своей собственной копией модельного состояния. Если отсутствие учета влияния параллельно работающих тестовых сценариев не может привести к ошибкам в оценке корректности поведения целевой системы, то тогда такой независимый запуск сценариев является корректным и может быть использован для того, чтобы удостовериться, что такие параллельные активности в целевой системе не приводят к аномальному поведения.
Следующий уровень параллелизма может быть достигнут при параллельном запуске нескольких сценарных функций в рамках одного тестового сценария. Одним из вариантов в рамках данного подхода является алгоритм повторного обхода графа сценария, предложенный в [28]. Идея этого алгоритма заключается в разбиении работы тестового сценария на две фазы. Первая фаза представляет собой обычную работу асинхронного тестового сценария dfsm, по результатам которой осуществляется построение графа тестового сценария. Во время второй фазы выполняется повторный обход графа сценария, во время которого в каждой вершине графа происходит параллельное выполнение всех пар сценарных функций с учетом дополнительных условий их допустимости.
Другим вариантом организации параллельной работы сценарных функций может быть комбинация нескольких тестовых сценариев, работающих с общим модельным состоянием. В этом случае работа теста также должна выполняться в двух режимах. В одном режиме работает только одна сценарная функция одного из сценариев, а в другом происходит параллельный запуск нескольких сценарных функций.
Общий недостаток рассмотренных выше подходов заключается в слишком большом удалении уровня параллелизма от целевой системы. Параллелизм на уровне тестовых сценариев и сценарных функций не может гарантировать параллельного выполнения функций целевой системы и, таким образом, не позволяет обеспечить даже минимального уровня тестирования одновременной работы компонентов целевой системы.
Возможность одновременной работы компонентов целевой системы и способы внешнего управления такой работой являются индивидуальными для каждой конкретной целевой системы. Поэтому для обеспечения эффективных параллельных воздействий на целевую систему предлагается использовать специальный управляющий механизм, зависящий от особенностей конкретной тестируемой системой.
Обращения к такому управляющему механизму можно осуществлять непосредственно из асинхронных сценарных функций. В результате разработчик тестового сценария получает возможность управлять не только набором модельных воздействий, предназначенным для одновременного выполнения, но и перебирать различные параметры такого выполнения.
Рассмотрим пример системы с асинхронным интерфейсом, в которой асинхронность проявляется как возможность блокировки вызовов отдельных интерфейсных функций вплоть до наступления некоторого события, например, вызова другой интерфейсной функции системы в параллельном потоке управления. Такая целевая система предполагает работу с общими данными из различных потоков управления. Поэтому проверка корректности синхронизации доступа к общим данным является необходимой составляющей качественного тестирования. Для осуществления такой проверки требуется организовать параллельное выполнение кода, осуществляющего доступ к общим данным, в нескольких потоках управления и обеспечить переключение этих потоков в процессе выполнения тестируемого кода.
В данном примере, управляющий механизм может быть построен на основе имеющейся информации о работе планировщика потоков операционной системы. В качестве указаний со стороны сценарных функций механизм может получать набор целевых функций, которые необходимо выполнять параллельно, а также итерируемые значения параметров, управляющих переключениями потоков.
Таким образом, предлагается отказаться от разработки универсального способа организации параллельных воздействий, так как нет оснований полагать, что такой метод может обеспечить требуемый уровень качества тестирования. Вместо этого предлагается разрабатывать специализированные механизмы организации параллельных воздействий, общие для определенных классов целевых систем, и обращаться к этим механизмам непосредственно из сценарных функций.
Такое решение оказывает минимальное влияние на архитектуру тестового набора. Оно влечет появление опционального компонента, ответственного за организацию параллельных воздействий. Через этот компонент некоторые асинхронные сценарные функции могут управлять генерацией тестовых воздействия, в то время как другие сценарные функции могут осуществлять тестовые воздействия самостоятельно.