Оценка качества тестирования
Мы рассмотрели, как работает тестовая система в масштабе одного взаимодействия с целевой системой и как организуется последовательность таких взаимодействий. При этом в тени осталась одна очень важная проблема, имеющая место в любом процессе тестирования - проблема оценка качества тестирования.
В подавляющем большинстве случаев проверить целевую систему на всех допустимых тестовых данных невозможно. Поэтому приходится ограничиваться некоторым конечным набором тестов. В такой ситуации неизбежно встает вопрос о качестве тестирования, проведенного посредством данного тестового набора.
Существует несколько подходов к решению этой задачи. Наиболее распространенный из них использует оценку качества на основе исходного кода целевой системы. Например, оценивается процент инструкций выполненных во время тестирования или процент покрытия возможных ветвлений потока управления.
Этот подход доказал свою важность и значимость. Однако, использование только оценки покрытия исходного кода применительно к функциональному тестированию часто оказывается недостаточным. Например, стопроцентное покрытие тестами исходного кода не гарантирует, что все требования к функциональности системы были надлежащим образом реализованы. Если какое-то требование было упущено и не нашло своего отражения в исходном коде, то тесты могут показывать идеальный процент покрытия, хотя в системе присутствует серьезный изъян.
С другой стороны, функциональное тестирование имеет своей целью проверить выполнение целевой системой требований, предъявляемых к ее функциональности. Поэтому измерение качества тестов, сформулированное в терминах этих требований, также является необходимым для получения адекватной оценки. Технология UniTesK предлагает именно такой подход, измерение качества тестирования в котором основывается на требованиях к функциональности системы.
Модель требований представляет собой абстрактный автомат A = ( V, X, Y, E ). Для оценки покрытия при тестировании конечных автоматов традиционно используются оценки числа покрытых состояний или переходов по сравнению с их общим числом. Но так как абстрактный автомат, как правило, является бесконечным, то такие методы оценки покрытия оказываются неприемлемыми. Для решения этой проблемы в технологии UniTesK используются метрики покрытия модели требований.
Метрики покрытия модели требований
Метрикой покрытия модели требований A =
( V, X, Y, E
) называется конечное множество подмножеств переходов модели требований M

2
E .
Элементами покрытия называются элементы метрики M, являющиеся подмножествами E.
Будем говорить, что тест { ( vi, xi, yi, v'i ) } покрыл элемент покрытия Cj  M, если тест содержит хотя бы одно взаимодействие ( vi, xi, yi, v'i ) входящее во множество Cj. Покрытием метрики M тестом { ( vi, xi, yi, v'i ) } будем называть набор элементов метрики M, покрытых данным тестом.
M, если тест содержит хотя бы одно взаимодействие ( vi, xi, yi, v'i ) входящее во множество Cj. Покрытием метрики M тестом { ( vi, xi, yi, v'i ) } будем называть набор элементов метрики M, покрытых данным тестом.
Таким образом, метрика покрытия определяет конечный набор элементов, в терминах которых осуществляется оценка качества тестирования. В технологии UniTesK некоторые метрики генерируются автоматически на основе структуры постусловий интерфейсных функций. В дополнение к этим метрикам, разработчик тестов может определять свои собственные метрики покрытия. Тестовая система автоматически оценивает качество тестирования в терминах всех доступных метрик и по результатам теста генерирует отчеты о покрытии элементов каждой метрики.
Метрика покрытия M называется управляемой, если для любых двух взаимодействий I1 = ( v1, x1, y1, v'1 ) и I2 = ( v2, x2, y2, v'2 ) выполнено следующее утверждение:
(v1 = v2) 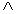 (x1 = x2)
(x1 = x2)  (
(  Ci
Ci  M (I1
M (I1  Ci)
Ci)  (I2
(I2  Ci) )
Ci) )
Для управляемых метрик характерно то, что принадлежность взаимодействия к тому или иному элементу покрытия зависит только от той части взаимодействия, которая управляется тестовой системой, то есть от пресостояния и стимула. Работая с управляемыми метриками, тестовая система может не только автоматически подсчитывать их покрытие, но и оптимизировать генерацию тестовых данных для достижения определенного покрытия по некоторой управляемой метрике.
Описание метрик покрытия
Метрики покрытия в технологии UniTesK описываются совместно с описанием предусловий и постусловий интерфейсных операций целевой системы. Это позволяет локализовать описание требований и выделение элементов покрытия на основе этих требований. Элементы покрытия, как правило, соответствуют ветвям функциональности в поведении интерфейсной операции или ситуациям, интересным с точки зрения тестирования, таким как граничные условия.
Определение метрик только для интерфейсных операций не позволяет описывать произвольные метрики покрытия модели требований. Но практический опыт показал, что имеющихся возможностей более чем достаточно для измерения качества тестирования приложений любых типов.
Определим способ описания метрик формально. Предположим, что в целевой системе выделено k интерфейсных операций: I = { Ii | i = 1, … , k } и требования к ее поведению были описаны в спецификации Spec = { SpecIi | i = 1, …, k }.
Тогда сюрьективная функция μ : VI x XI x YI x VI  R называется метрикой покрытия интерфейсной операции I с сигнатурой ( In, Out, Var ) 6, если множество R является конечным. Каждой метрике покрытия интерфейсной операции μ соответствует метрика покрытия модели требований MR[Spec], которую мы будем обозначать M[μ].
R называется метрикой покрытия интерфейсной операции I с сигнатурой ( In, Out, Var ) 6, если множество R является конечным. Каждой метрике покрытия интерфейсной операции μ соответствует метрика покрытия модели требований MR[Spec], которую мы будем обозначать M[μ].
M[μ] = { Cr  2E | r
2E | r  R }, где Cr = { ( v, x, y, v' )
R }, где Cr = { ( v, x, y, v' )  V x X x Y x V | μ( v, x, y, v' ) = r}.
V x X x Y x V | μ( v, x, y, v' ) = r}.
Лемма.
Метрика покрытия M[μ] является управляемой тогда и только тогда, когда третий и четвертый аргументы функции μ являются несущественными.
Кроме того, в технологии UniTesK поддерживается другой вариант описания метрик покрытия. В этом варианте каждый элемент покрытия описывается предикатом, определяющим принадлежность взаимодействия через определенную интерфейсную операцию ( v, x, y, v' ) к данному элементу покрытия. Такой способ описания позволяет задавать метрики покрытия модели требований, элементы которых могут пересекаться между собой. Но, как и в первом способе, существуют ограничения на описываемые метрики, связанные с привязкой каждой метрики только к одной интерфейсной операции.
Конечный набор предикатов μ' = { ci | i = 1, … , m; ci : VI x XI x YI x VI  Bool } называется расширенной метрикой покрытия интерфейсной операции I с сигнатурой ( In, Out, Var ). Каждой расширенной метрике покрытия интерфейсной операции μ' соответствует метрика покрытия модели требований MR[Spec], которую мы будем обозначать M[μ'].
Bool } называется расширенной метрикой покрытия интерфейсной операции I с сигнатурой ( In, Out, Var ). Каждой расширенной метрике покрытия интерфейсной операции μ' соответствует метрика покрытия модели требований MR[Spec], которую мы будем обозначать M[μ'].
M[μ'] = { Ci  2E | i = 1, … , m }, где Ci = { ( v, x, y, v' )
2E | i = 1, … , m }, где Ci = { ( v, x, y, v' )  V x X x Y x V | ci( v, x, y, v' ) }.
V x X x Y x V | ci( v, x, y, v' ) }.
Лемма.
Метрика покрытия M[μ'] является управляемой тогда и только тогда, когда третий и четвертый аргументы всех предикатов ci являются несущественными.
Метрики покрытия в унифицированной архитектуре теста
В процессе тестирования, при вызове интерфейсной операции, тестовая система вычисляет для каждой метрики, заданной для данной операции, все элементы покрытия, покрытые данным вызовом. Информация о покрытых элементах попадает в
трассу теста. По трассе одного или нескольких тестов генерируются отчеты о покрытии интерфейсных операций, согласно определенным для них метрикам покрытия.
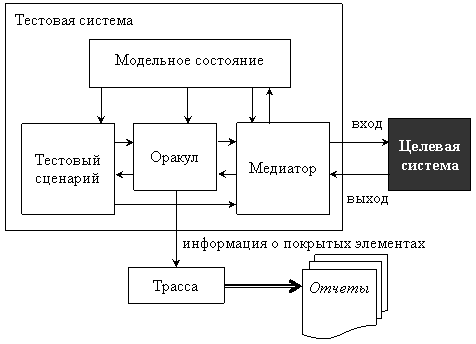
Рисунок 8. Универсальная архитектура теста с учетом оценки качества тестирования
Компонент тестовой системы, который отвечает за вычисление покрытых элементов в рамках одного вызова интерфейсной операции, - оракул. Он обладает всей информацией, необходимой для выполнения этого действия. Для известных ему пресостояния, стимула, реакции и постсостояния оракул вычисляет покрытые элементы и помещает результат вычисления в трассу. Для метрики покрытия, описанной функцией μ, оракул вычисляет значение этой функции, которое однозначно характеризует покрытый элемент. Для расширенной метрики покрытия оракул вычисляет значения всех предикатов ci и индексы предикатов, принявших положительное значение, помещаются в трассу в качестве описания покрытых элементов.
Помимо информации о покрытых элементах в трассу попадает информация о вызовах интерфейсных операций, значениях их параметров, вердиктах оракула, а также о других событиях, произошедших в процессе тестирования. По завершении процесса тестирования трасса используется для анализа результатов тестирования. На ее основе генерируются отчеты о покрытии, отчеты о найденных несоответствиях между поведением целевой системы и требованиями к нему, а также отчеты об ошибках, имевших место в тестовой системе.
Архитектура тестовой системы, дополненная работой с метриками покрытия, представлена на рисунке 8.
Управляемые метрики покрытия и оптимизация тестового набора
Помимо статической оценки качества тестирования управляемые метрики покрытия используются для оптимизации генерации тестовых данных непосредственно во время тестирования. Технология UniTesK предоставляет возможность не только складывать информацию о покрытии в трассу, но и использовать ее в процессе работы теста.
Предположим, что перед тестом стоит задача достичь определенного уровня покрытия по некоторому набору метрик. В этом случае тесту не имеет смысла подавать целевой системе стимулы, которые не приводят к улучшению покрытия. Чтобы оптимизировать таким образом тестовый набор, достаточно собирать в глобальном состоянии сценария информацию о покрытых элементах и отбрасывать в сценарных функциях те стимулы, которые не приводят к улучшению покрытия.
Унифицированная архитектура теста
В предыдущих разделах мы определили математические модели, используемые в технологии UniTesK. Также мы рассмотрели, как эти модели отражаются в унифицированной архитектуре теста. А теперь мы взглянем на унифицированную архитектуру в целом, соединив все разрозненные описания в единое целое.
Унифицированная архитектура теста в целом представлена на рисунке 9. Она определяет набор компонентов теста, составляющих ядро тестовой системы. Помимо тестовой системы, на диаграмме представлены:
- целевая система - программная система, которую необходимо протестировать,
- трасса - набор информации о ходе тестирования, собираемой тестовой системой во время работы теста,
- отчеты - набор отчетов о различных аспектах процесса тестирования, генерируемый инструментами семейства UniTesK, на основе трассы теста.
Тестовая система содержит четыре компонента.
Тестовый сценарий управляет всем процессом тестирования. Он интерактивно, в ходе взаимодействия с целевой системой, генерирует последовательность воздействий на целевую систему. Для этого автоматный механизм осуществляет обход графа, заданного в описании сценария. Прохождение по дуге этого графа сопровождается выполнением сценарного воздействия, приписанного данной дуге. Сценарное воздействие, которое является "компактным" тестовым сценарием, управляет последовательностью взаимодействий с целевой системой. По завершению работы сценарного воздействия автоматный механизм либо принимает решение о завершении тестирования, либо выбирает следующую дугу и инициирует следующее сценарное воздействие.
Все воздействия на целевую систему генерируемые тестовым сценарием осуществляется через оракул. Оракул
- проверяет допустимость данного воздействия в текущем модельном состоянии,
- выполняет это воздействие посредством обращения к медиатору,
- проверяет корректность поведения целевой системы в рамках данного взаимодействия,
- вычисляет покрытые элементы для всех заданных метрик покрытия и помещает эту информацию в трассу теста.
Медиатор получает от оракула указание осуществить тестовое воздействие, заданное стимулом x  X. Для решения этой задачи медиатор
X. Для решения этой задачи медиатор
- преобразует стимул x в вызов интерфейсной функции целевой системы со значениями входных параметров, соответствующих данному стимулу, и осуществляет этот вызов,
- получает ответную реакцию целевой системы,
- преобразует ее в модельное представление - некоторую реакцию y
 Y,
Y,
- синхронизирует модельное состояние с внутренним состоянием тестируемой системы после оказания тестового воздействия,
- возвращает модельное представление ответной реакции y
 Y оракулу.
Y оракулу.
Единственный пассивный компонент тестовой системы - это модельное состояние. Основная задача модельного состояния заключается в хранении текущих значений переменных состояния, определенных в спецификации целевой системы. Эти значения составляют модельное представление внутреннего состояния целевой системы. Поэтому только медиатор, который непосредственно работает с целевой системой, может изменять модельное состояние. Все остальные компоненты могут только читать модельное состояние.
3. Тестирование систем с асинхронным интерфейсом
Настоящая глава начинается с определение систем с асинхронным интерфейсом и выделения ограничений рассмотренных методов и моделей, которые не позволяют использовать их для проведения полноценного тестирования систем с асинхронным интерфейсом. Далее будут определены математические модели, которые позволяют корректным образом сформулировать основные задачи тестирования для систем с асинхронным интерфейсом, и рассмотрены алгоритмы, решающие эти задачи. На основе предложенных моделей и алгоритмов будет построена унифицированная архитектура асинхронной тестовой системы, определяющая архитектуру всех тестовых систем, предназначенных для тестирования систем с асинхронным интерфейсом рассматриваемым методом.
Системы с асинхронным интерфейсом
Основополагающим камнем в математических моделях технологии UniTesK являются понятия взаимодействия и модели поведения целевой системы. Именно в этих терминах описывается процесс тестирования и на их основе строятся все остальные модели.
Однако, у данных моделей есть несколько ограничений. Во-первых, в них предполагается, что любое взаимодействие между целевой системой и ее окружением может инициироваться только окружением. Во-вторых, предполагается, что все взаимодействия происходят строго последовательно, то есть следующее взаимодействие начинается только после завершения предыдущего.
Примером целевой системы, для которой эти предположения нарушаются, является подсистема, реализующая стек протоколов. Она получает пакеты от вышестоящего уровня, формирует из них пакеты нижележащего уровня и посылает по сети. С другой стороны, эта подсистема получает пакеты из сети, преобразует их и передает вышестоящему приложению.
Передача пакетов в сеть и приложению являются примерами взаимодействий, которые инициируются не окружением, а самой целевой системой. Конечно, эти взаимодействия можно моделировать как часть взаимодействий, инициированных окружением. То есть можно рассматривать пакет, отправленный в сеть, как часть реакции на просьбу послать сообщение от приложения или как часть реакции на пришедший пакет из сети.
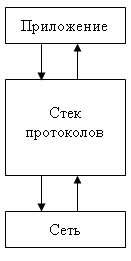
Рисунок 10. Стек протоколов
Но в этом случае особенно критичными становится второе ограничение. Рассмотрим взаимодействие, которое инициируется приложением вышестоящего уровня. Приложение просит стек протоколов послать сообщение. Завершением этого взаимодействия будем считать передачу в сеть всех пакетов, необходимых для посылки данного сообщения. Предположение о последовательности взаимодействий не позволяет тестовой системе инициировать следующее взаимодействие до завершения предыдущего. Таким образом, рассмотренная выше архитектура будет ограничена тестированием только тех ситуаций, в которых стек протоколов в каждый момент времени обрабатывает только один запрос о посылке сообщения.
Программные системы, для которых нарушаются вышеприведенные ограничения, наиболее часто встречаются среди драйверов устройств, телекоммуникационных приложений, подсистем, реализующих межпроцессное или межпотоковое взаимодействие, и других программ системного уровня. Такого рода программы характеризуются асинхронными взаимодействиями с окружением.
Программные системы, которые
- самостоятельно инициируют взаимодействия с окружением или
- могут одновременно участвовать в нескольких взаимодействиях с окружением
мы будем называть системами с асинхронным интерфейсом.
Технология UniTesK в рамках подхода классических программных контрактов может быть применима для тестирования систем с асинхронным интерфейсом, однако качество разработанных тестов будет ограничиваться тестированием только в последовательном, синхронном режиме. В следующих разделах настоящей главы мы рассмотрим решения, которые предлагает технология UniTesK для обеспечения полноценного тестирования систем с асинхронным интерфейсом.
Оценка корректности поведения тестируемой системы
Модель поведения
Основной задачей модели поведения целевой системы является адекватное описание поведения целевой системы с тем, чтобы тестовая система имела возможность оценить корректность этого поведения относительно требований, предъявляемых к нему.
Основным отличием систем с асинхронным интерфейсом являются
- взаимодействия, инициируемые целевой системой;
- возможность участия целевой системы в нескольких взаимодействиях одновременно.
Чтобы учесть взаимодействия, инициируемые целевой системой, мы расширим понятие интерфейса целевой системы.
Асинхронным интерфейсом целевой системы называется тройка ( X, Y, Z ), где
- X - множество стимулов,
- Y - множество реакций,
- Z - множество отложенных реакций.
Каждое из этих множеств может быть бесконечным.
Множество отложенных реакций Z предназначено для описания взаимодействий, инициируемых целевой системой.
Другое отличие в определении асинхронного интерфейса, по сравнению с синхронным, заключается в отсутствии множества состояний. Причина этого состоит в том, что при асинхронных взаимодействиях состояние целевой системы в общем случае является недоступным для внешнего наблюдения, так как оно может изменяться в любой момент ввиду участия в целевой системы в параллельных взаимодействиях.
Асинхронным воздействием на целевую систему, обладающую интерфейсом ( X, Y, Z ), называется пара ( x, y )  X x Y. Первый элемент воздействия x будем называть стимулом, а второй y - непосредственной реакцией.
X x Y. Первый элемент воздействия x будем называть стимулом, а второй y - непосредственной реакцией.
Асинхронной реакцией целевой системы, обладающей интерфейсом ( X, Y, Z ), называется элемент множества Z.
Асинхронные воздействия и асинхронные реакции будем называть асинхронными взаимодействиями с целевой системой.
Асинхронные взаимодействия с целевой системой разбиваются на два класса. Первый класс составляют взаимодействия, инициируемые тестовой системой. Их мы называем асинхронными воздействиями. Асинхронное воздействие состоит из стимула, моделирующего данные передаваемые от тестовой системе к целевой, и непосредственной реакции, содержащей данные передаваемые в обратном направлении в рамках того же взаимодействия.
Второй класс асинхронных взаимодействий содержит взаимодействия, инициируемые целевой системой. Такие взаимодействия мы называем асинхронными реакциями (или отложенными реакциями). Асинхронные реакции используются для моделирования данных передаваемых только в направлении от целевой системы.
Таким образом, моделировать взаимодействия с целевой системой предлагается следующим способом. Если взаимодействие инициируется окружением целевой системы, то для его описания используются асинхронные воздействия. При этом данные, передаваемые в направлении к целевой системе, описываются стимулом, а данные, передаваемые от целевой системы, описываются непосредственной реакцией.
Если взаимодействие инициируется целевой системой и данные в рамках этого взаимодействия передаются только в направлении от целевой системы, то такие взаимодействия моделируются асинхронными реакциями.
Если же взаимодействие инициируется целевой системой, но данные в рамках этого взаимодействия передаются и от целевой системы, и к ней, то при моделировании таких взаимодействий предлагается разбивать их на меньшие составляющие, которые описываются посредством асинхронных воздействий и асинхронных реакций. Например, такое взаимодействие можно разбить на асинхронную реакцию, инициируемую целевой системой, и на набор последующих асинхронных воздействий, включающих в себя данные, передаваемые к целевой системе.
| Вид |
Инициатор взаимодействия |
Направление передачи данных |
Способ моделирования |
| 1 |
Окружение целевой системы |
к целевой системе и от нее |
Асинхронное воздействие |
| 2 |
Целевая система |
только от целевой системы |
Асинхронная реакция |
| 3 |
Целевая система |
от целевой системы и к ней |
Асинхронная реакция и последующие асинхронные воздействия |
Таблица 1. Виды взаимодействий с целевой системой.
Суммарная информация по предлагаемым способам моделирования взаимодействий целевой системы с ее окружением представлена в таблице 1.
Определение 7.
Асинхронной моделью поведения целевой системы с интерфейсом ( X, Y, Z ) называется частично-упорядоченное мультимножество асинхронных взаимодействий ( P,  ).
).
Модель поведения состоит из, возможно, бесконечного набора асинхронных взаимодействий, имевших место в процессе тестирования. Частичный порядок, заданный на этом наборе, определяет, в каком порядке происходили взаимодействия. p1  p2 означает, что взаимодействие p1 произошло раньше, чем взаимодействие p2. Если взаимодействия несравнимы, то это значит, что их взаимный порядок - неизвестен.
p2 означает, что взаимодействие p1 произошло раньше, чем взаимодействие p2. Если взаимодействия несравнимы, то это значит, что их взаимный порядок - неизвестен.
Множество всех асинхронных моделей поведения целевой системы с интерфейсом ( X, Y, Z ) мы будем обозначать Ω( X, Y, Z ).
Модель требований
Автоматом с отложенными реакциями [
28] называется пятёрка
( V, X, Y, Z, E
), где
- V - множество состояний,
- X - множество стимулов,
- Y - множество непосредственных реакций,
- Z - множество отложенных реакций,
- E
 V x ( (X x Y)
V x ( (X x Y)  Z ) x V - множество переходов.
Z ) x V - множество переходов.
Множества V, X, Y, Z и E могут быть бесконечными.
Переходы автомата с отложенными реакциями делятся на два класса. В первый класс входят переходы ( v, ( x, y ), v' ), помеченные стимулом x и непосредственной реакцией y, а во второй - переходы ( v, z, v' ), помеченные отложенной реакцией z. Первый и последний элементы перехода ( v, p, v' ) мы будем называть пресостоянием и постсостоянием соответственно.
Последовательность переходов ( e1, e2, …, en ) автомата с отложенными реакциями A = ( V, X, Y, Z, E ) называется путем, если для каждого i = 1, …, n-1 постсостояние перехода ei совпадает с пресостоянием перехода ei+1. При этом мы будем говорить, что путь ведет из пресостояния перехода e1 в постсостояние перехода en.
Бесконечным путем мы будем называть бесконечную последовательность переходов, любой префикс которой является конечным путем.
Определение 8.
Асинхронной моделью требований к целевой системе с интерфейсом ( X, Y, Z ) называется автомат с отложенными реакциями, множества стимулов, непосредственных и отложенных реакций которого совпадают с X, Y и Z соответственно.
Будем говорить, что асинхронное взаимодействие p  (X x Y)
(X x Y)  Z является корректным относительно модели требований A = ( V, X, Y, Z, E ) в состоянии v
Z является корректным относительно модели требований A = ( V, X, Y, Z, E ) в состоянии v  V, если существует такое состояние v'
V, если существует такое состояние v'  V, что тройка ( v, p, v' ) принадлежит множеству переходов E.
V, что тройка ( v, p, v' ) принадлежит множеству переходов E.
Определение 9.
Будем говорить, что асинхронная модель поведения целевой системы ( P,  ) удовлетворяет асинхронной модели требований A = ( V, X, Y, Z, E ) с начальным состоянием v0
) удовлетворяет асинхронной модели требований A = ( V, X, Y, Z, E ) с начальным состоянием v0  V, если существует конечный или бесконечный путь ( e1, e2, …, en, … ) в автомате A такой, что:
V, если существует конечный или бесконечный путь ( e1, e2, …, en, … ) в автомате A такой, что:
- пресостояние перехода e1 совпадает с состоянием v0,
- существует взаимнооднозначное соответствие κ между мультимножеством P и мультимножеством переходов { ei }, такое что:
- для каждого элемента p
 P второй элемент перехода κ( p ) совпадает с p,
P второй элемент перехода κ( p ) совпадает с p,
- для любой пары p1, p2
 P из p1
P из p1  p2 следует, что индекс перехода κ( p1) в пути меньше индекса перехода κ( p2).
p2 следует, что индекс перехода κ( p1) в пути меньше индекса перехода κ( p2).
Другими словами, асинхронная модель поведения удовлетворяет модели требований с данным начальным состоянием, если взаимодействия из мультимножества P можно упорядочить, не вступая в противоречие с частичным порядком  , таким образом, чтобы в автомате с отложенными реакциями нашелся путь, помеченный данными взаимодействиями в данном порядке и начинающийся в данном начальном состоянии.
, таким образом, чтобы в автомате с отложенными реакциями нашелся путь, помеченный данными взаимодействиями в данном порядке и начинающийся в данном начальном состоянии.
Важно отметить, что асинхронная модель требований предполагают, что для любого набора взаимодействий, осуществлявшихся параллельно, существует эквивалентное с точки зрения конечного результата последовательное выполнение этих взаимодействий. Если данная гипотеза, называемая гипотезой простого параллелизма [20], не выполняется, то необходимо разбить взаимодействия на более мелкие, для которых гипотеза будет верна. Если никакое разбиение не позволяет добиться выполнения данной гипотезы, то рассматриваемый метод является неприменимым для тестирования такой системы. На настоящий момент автору неизвестен пример программной системы, для которой невозможно выбрать асинхронный интерфейс, удовлетворяющий гипотезе простого параллелизма.
Проверка наличия отношения "удовлетворяет" для асинхронных моделей значительно сложнее, по сравнению с синхронным случаем. Поэтому необходимо провести дополнительный анализ алгоритма этой проверки. Но прежде чем рассматривать этот алгоритм, мы остановимся на способах описания модели требований и модели поведения, так как способы задания моделей оказывают существенное влияния на алгоритмы работы с ними.
Описание асинхронной модели требований
Для описания асинхронных моделей требований используется немного модифицированный подход программных контрактов. Основные идеи этого способа состоят в следующем.
Для целевой системы проводится анализ ее интерфейса. В ходе анализа выявляются виды взаимодействий, в которых целевая система может принимать участие, и их параметры. Для каждого вида определяется, кто является инициатором взаимодействия данного вида, и какие данные передаются в ходе взаимодействия по направлению к целевой системе, а какие - от нее.
При этом накладывается ограничение на взаимодействия, инициируемые целевой системой. В процессе таких взаимодействий данные должны передаваться только от целевой системы. Если это ограничение не выполняется, то необходимо разбить проблемные взаимодействия на меньшие составляющие.
В результате мы получим набор взаимодействий, инициируемых окружением целевой системы, и набор взаимодействий, инициируемых целевой системой. Взаимодействия первого типа имеют данные, передаваемые к целевой системе, мы будем называть их входными, и данные, передаваемые от целевой системы, мы будем называть их выходными. Взаимодействия второго типа содержат только данные, передаваемые от целевой системы, которые мы также будем называть выходными.
Каждому виду взаимодействий ставится в соответствие интерфейсная операция. Для взаимодействий первого типа интерфейсная операция имеет набор входных параметров, описывающих входные данные, и набор выходных параметров, описывающих выходные данные. Такие интерфейсные операции мы будем называть интерфейсными операциями-стимулами. Для взаимодействий второго типа интерфейсная операция имеет только выходные параметры, описывающие выходные данные. Интерфейсные операции такого типа мы будем называть интерфейсными операциями-реакциями.
Для описания требований к поведению целевой системы в рамках асинхронных взаимодействий используется спецификации соответствующих интерфейсных операций. Предусловие операции определяет, какие значения входных параметров являются допустимыми для передачи целевой системе, а постусловие операции определяет какие выходные значения параметров являются корректными для данных значений входных параметров. Таким образом, постусловие описывает требования к поведению целевой системы в ходе взаимодействий данного вида.
Для описания зависимости поведения в рамках данного взаимодействия от предыдущих взаимодействий используется модельное состояние. Модельное состояние образуется набором переменных, хранящих все необходимые для этого данные об истории взаимодействий с целевой системой.
Предположим, что для целевой системы были выделены k видов взаимодействий, инициируемых окружением, и m видов взаимодействий, инициируемых целевой системой. Тогда асинхронной спецификацией целевой системы называется набор спецификаций интерфейсных операций, соответствующих каждому выделенному виду взаимодействий: { SpecSi | i = 1, …, k; k > 0 }  { SpecRj | j = 1, …, m; m ≥ 0 }.
{ SpecRj | j = 1, …, m; m ≥ 0 }.
Асинхронная модель требований MRA[Spec] = ( V, X, Y, Z, E ), которая описывается данной асинхронной спецификацией Spec = { SpecSi | i = 1, …, k; k > 0 }  { SpecRj | j = 1, …, m; m ≥ 0 } определяется согласно следующим правилам:
{ SpecRj | j = 1, …, m; m ≥ 0 } определяется согласно следующим правилам:
- если в спецификации присутствует хотя бы одна переменная состояния, то множество состояний V является декартовым произведением множеств допустимых значений всех переменных состояния
V = 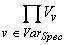 ,
,
где VarSpec является объединением переменных состояния всех интерфейсных
операций, принадлежащих спецификации
VarSpec = 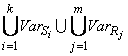 .
.
- если в спецификации не участвует ни одной переменной состояния, то множество состояний состоит из единственного элемента ε:
V = { ε }.
- множество стимулов X является дизъюнктивным объединением декартовых произведений множеств допустимых значений входных параметров всех интерфейсных операций-стимулов спецификации
X = 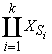 .
.
Мы будем считать, что каждый элемент дизъюнктивного объединения
помечается именем интерфейсного операций и таким образом эти элементы не
пересекаются между собой.
- множество непосредственных реакций Y является дизъюнктивным объединением декартовых произведений множеств допустимых значений выходных параметров всех интерфейсных операций-стимулов спецификации
Y = 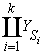 .
.
Мы будем считать, что каждый элемент дизъюнктивного объединения
помечается именем интерфейсного операций и таким образом эти элементы не
пересекаются между собой.
- множество отложенных реакций Z является дизъюнктивным объединением декартовых произведений множеств допустимых значений выходных параметров всех интерфейсных операций-реакций спецификации
Z = 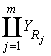 .
.
Мы будем считать, что каждый элемент дизъюнктивного объединения
помечается именем интерфейсной операции и таким образом эти элементы не
пересекаются между собой.
- множество переходов E состоит из всех переходов, удовлетворяющих обобщенным предусловию и постусловию спецификации
E = { ( v, ( x, y ), v' )  V x ( (X x Y)
V x ( (X x Y)  Z ) x V | preS( v, x )
Z ) x V | preS( v, x ) 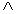 postS( v, x, y, v' ) }
postS( v, x, y, v' ) }
 { ( v, z, v' )
{ ( v, z, v' )  V x ( (X x Y)
V x ( (X x Y)  Z ) x V | preR( v )
Z ) x V | preR( v ) 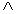 postR( v, z, v' ) },
postR( v, z, v' ) },
где предикаты preS = 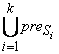 , postS =
, postS = 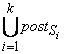 , preR =
, preR =  , postR =
, postR = 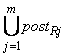 .
.
Описание асинхронных взаимодействий в модели поведения
Как и в синхронном случае, модель поведения целевой системы не может быть описана статическим образом. Только динамически, во время тестирования, тестовая система наблюдает за поведением целевой системы и строит модель этого поведения.
Чтобы модель поведения была согласована с моделью требований, необходимо чтобы она была построена на основе единого интерфейса целевой системы ( X, Y, Z ). Если модель требований задана спецификацией Spec, то таким образом интерфейс целевой системы ( X, Y, Z ) фиксирован согласно определению MRA[Spec]. Стимул задается интерфейсной операцией-стимулом и набором значений входных параметров этой операции, непосредственная реакция идентифицируется интерфейсной операцией-стимулом и набором значений выходных параметров этой операции, а отложенная реакция идентифицируется интерфейсной операцией-реакцией и набором значений выходных параметров этой операции.
В этом случае асинхронная модель поведения целевой системы определяется в терминах заданной спецификации. Асинхронная модель поведения состоит из набора асинхронных взаимодействий и частичного порядка над ним. Набор взаимодействий определяется посредством регистрации всех зафиксированных взаимодействий в специальном компоненте тестовой системы - регистраторе взаимодействий. А частичный порядок над этим набором задается посредством комбинации двух моделей: модели каналов и модели временных меток.
Асинхронные взаимодействия, инициированные тестовой системой, регистрируются после получения непосредственной реакции от целевой системы. Такие взаимодействия характеризуются:
- идентификатором интерфейсной операции-стимула,
- набором значений входных параметров этой операции,
- набором значений выходных параметров этой операции.
Асинхронные взаимодействия, инициированные целевой системой, регистрируются после их завершения. Такие взаимодействия характеризуются:
- идентификатором интерфейсной операции-реакции,
- набором значений выходных параметров этой операции.
Способы задания частичного порядка над мультимножеством асинхронных взаимодействий мы рассмотрим в следующих двух разделах.
Модель каналов
Модель каналов предназначена для задания частичного порядка на наборе асинхронных взаимодействий.
Определение 10.
Пусть D - конечное или бесконечное множество. Моделью каналов на множестве D мы будем называть конечное или бесконечное множество упорядоченных подмножеств множества D Ch = { ( Di, <i ) | i = 1, …, n, … }, такое что
- подмножества Di взаимно не пересекаются (
 i, j i ≠ j
i, j i ≠ j  Di
Di 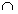 Dj = Ø),
Dj = Ø),
- объединение всех подмножеств дает множество D (
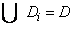 ).
).
Модель каналов задает частичный порядок на множестве D, определяемый следующим образом:
d1  Ch d2
Ch d2 
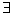 i: d1 <i d2.
i: d1 <i d2.
Множества Di модели каналов мы будем называть каналами.
Модель каналов во многих случаях является удобным механизмом для задания частичного порядка, так как она позволяет описывать наиболее естественным способом порядок взаимодействий, происходивших в одном "канале".
Например, если сетевой протокол, с помощью которого осуществляется взаимодействие, обеспечивает сохранение порядка сообщений, то все сообщения посылаемые через один "сокет" на другой "сокет" между собой строго упорядочены. Тем не менее, никакой информации о порядке доставки этих сообщений относительно сообщений, посылаемых по другим парам "сокетов", не известно.
В таких ситуациях, модель каналов позволяет отнести все упорядоченные сообщения к одному каналу и задать для этого канала соответствующий порядок. Чтобы сделать это, при регистрации каждого взаимодействия в тестовой системе предлагается указывать в качестве одной из характеристик взаимодействия - идентификатор канала, к которому относится данное взаимодействие. Порядок взаимодействий в рамках одного канала задается порядком регистрации взаимодействий. Считается, что взаимодействие, которое было зарегистрировано раньше другого, относящегося к тому же каналу, произошло раньше, чем второе.
Но одной модели каналов оказывается недостаточно для описания произвольного частичного порядка. Поэтому существует еще один механизм для определения частичного порядка на асинхронной модели поведения целевой системы.
Модель временных меток
Модель временных меток предназначена для возможности задания дополнительных ограничений на порядок взаимодействий в асинхронной модели поведения целевой системы.
Пусть ( TM,  TM ) - частично-упорядоченное множество временных меток. Тогда временным интервалом мы будем называть пару временных меток ( tm1, tm2 ), в которой вторая метка больше либо равна первой (т.е. tm1 = tm2
TM ) - частично-упорядоченное множество временных меток. Тогда временным интервалом мы будем называть пару временных меток ( tm1, tm2 ), в которой вторая метка больше либо равна первой (т.е. tm1 = tm2 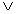 tm1
tm1  TM tm2).
TM tm2).
Множество всех временных интервалов будет обозначаться TI(TM). Определим на нем частичный порядок  TI следующим образом:
TI следующим образом:
( tm1, tm2 )  TI ( tm'1, tm'2 )
TI ( tm'1, tm'2 )  tm2
tm2  TM tm'1
TM tm'1
Определение 11.
Пусть D - конечное или бесконечное множество, а ( TM,  TM ) - множество временных меток. Тогда моделью временных меток на множестве D мы будем называть отображение τ : D
TM ) - множество временных меток. Тогда моделью временных меток на множестве D мы будем называть отображение τ : D  TI(TM).
TI(TM).
Модель временных меток задает на множестве D частичный порядок  τ :
τ :
d1  τ d2
τ d2  τ(d1)
τ(d1)  TI τ(d2).
TI τ(d2).
В качестве множества временных меток TM в технологии UniTesK используется множество (F x Nat)  { -∞, +∞ }, где F - конечное или бесконечное множество систем координат, Nat - множество натуральных чисел, а -∞ и +∞ - специально выделенные значения.
{ -∞, +∞ }, где F - конечное или бесконечное множество систем координат, Nat - множество натуральных чисел, а -∞ и +∞ - специально выделенные значения.
Для описания частичного порядка  TM применяются следующие правила:
TM применяются следующие правила:
 f
f  F
F  n
n  Nat -∞
Nat -∞  TM ( f, n ),
TM ( f, n ),
 f
f  F
F  n
n  Nat ( f, n )
Nat ( f, n )  TM +∞,
TM +∞,
 f
f  F
F  n1,n2
n1,n2  Nat n1 < n2
Nat n1 < n2  ( f, n1 )
( f, n1 )  TM ( f, n2 ),
TM ( f, n2 ),
 f1,f2
f1,f2  F
F  n1,n2
n1,n2  Nat ( f1, n1 )
Nat ( f1, n1 )  TM ( f2, n2 ), если эта зависимость была зафиксирована разработчиком теста и она не противоречит определению частичного порядка (иррефлексивность, антисимметричность и транзитивность).
TM ( f2, n2 ), если эта зависимость была зафиксирована разработчиком теста и она не противоречит определению частичного порядка (иррефлексивность, антисимметричность и транзитивность).
Для установки зависимостей последнего типа тестовая система предоставляет специальную функцию, с помощью которой в процессе тестирования можно зафиксировать зависимости между временными метками. Множество систем координат F также определяется динамически, в процессе тестирования.
Модель временных меток предоставляет удобный способ для описания частичного порядка на множестве взаимодействий при использовании в следующей интерпретации. Временная метка рассматривается как идентификатор некоторого момента времени. Каждый момент времени описывается натуральным числом в некоторой системе временных координат. В рамках одной системы координат все моменты времени упорядочены. А про моменты времени, принадлежащие различным системам координат, заранее ничего не известно. Но если какая-нибудь информация появляется, то она фиксируется согласно четвертому правилу.
Каждому взаимодействию ставится в соответствие временной интервал, первая временная метка, которого описывает момент начала взаимодействия, а вторая - момент его завершения. Таким образом, считается, что одно взаимодействие достоверно произошло раньше другого, если временная метка завершения первого взаимодействия меньше временной метки начала второго. В качестве концов интервала допускается использование специальных значений -∞ и +∞, предназначенных для описания открытых интервалов.
Способ выделения натуральных чисел, используемых для описания момента времени, может варьироваться. Это может быть текущее значение системного таймера или просто некоторое абстрактное число. Различные системы временных координат, например, могут соответствовать различным машинам в сети.
Определять модель временных меток предлагается следующим образом. Во-первых, в процессе тестирования фиксируется информация об отношении порядка между временными метками, принадлежащими различным системам координат. А во-вторых, при регистрации взаимодействий указывается временной интервал, соответствующий данному взаимодействию.
Описание асинхронной модели поведения
Суммируя информацию о построении асинхронной модели поведения целевой системы в процессе тестирования, можно сказать, что этот процесс состоит из решения двух задач:
- регистрации взаимодействий,
- фиксирования достоверно известной информации о порядке, в котором происходили эти взаимодействия.
Регистрация взаимодействий осуществляется в специальном компоненте тестовой системы - регистраторе взаимодействий. А для решения второй задачи предлагается при регистрации взаимодействий указывать идентификатор канала, к которому относится данное взаимодействие, и временной интервал, в котором оно происходило. Кроме того, требуется фиксировать известные ограничения на порядок временных меток, принадлежащих различным системам координат.
В результате этого тестовая система будет иметь набор асинхронных взаимодействий D, модель каналов Ch и модель временных меток τ. На основе этой информации будет построена асинхронная модель поведения ( P,  ), в которой
), в которой
- мультимножество взаимодействий P совпадает с D,
- частичный порядок π является транзитивным замыканием объединения частичных порядков
 Ch и
Ch и  τ.
τ.
Алгоритм проверки корректности поведения
Предположим, что нам даны конечная асинхронная модель поведения целевой системы
( P,
 )
) и асинхронная модель требований A =
( V, X, Y, Z, E
) с начальным состоянием v
0 
V. Как проверить, находятся ли эти модели в отношении "удовлетворяет" или нет?
Для этого необходимо проверить существование пути ( e1, e2, …, en ) в автомате A, начинающегося в состоянии v0 и помеченного взаимодействиями из P так, чтобы это не противоречило частичному порядку π.
Асинхронная модель требований A = ( V, X, Y, Z, E ) задается асинхронной спецификацией { SpecSi | i = 1, …, k; k > 0 }  { SpecRj | j = 1, …, m; m ≥ 0 }, которая определяет переходы автомата неявным образом. Это осложняет решение поставленной задачи, так как вычисление состояний, в которые можно попасть из данного состояния по переходам помеченным данным символом, сводится к решению системы уравнений.
{ SpecRj | j = 1, …, m; m ≥ 0 }, которая определяет переходы автомата неявным образом. Это осложняет решение поставленной задачи, так как вычисление состояний, в которые можно попасть из данного состояния по переходам помеченным данным символом, сводится к решению системы уравнений.
В данном разделе мы не будем рассматривать пути решения этой проблемы. Здесь мы будем считать, что нам задана вспомогательная функция γ : V x ( (X x Y)  Z )
Z )  2V , вычисляющая множество состояний, которые модель требований допускает в качестве постсостояния перехода с данным пресостоянием v и асинхронным взаимодействием p:
2V , вычисляющая множество состояний, которые модель требований допускает в качестве постсостояния перехода с данным пресостоянием v и асинхронным взаимодействием p:
γ( v, p ) = { v'  V | ( v, p, v' )
V | ( v, p, v' )  E }
E }
Но даже в этом случае для проверки корректности поведения требуется рассмотреть все возможные линеаризации асинхронной модели поведения и для каждой из них проверить существование соответствующего пути в автомате A.
Определение 12.
Линейный порядок < на частично-упорядоченном множестве ( P,  ) называется линеаризацией, если он сохраняет частичный порядок
) называется линеаризацией, если он сохраняет частичный порядок  , то есть
, то есть
 p1, p2
p1, p2  P p1
P p1  p2
p2  p1 < p2.
p1 < p2.
Для последующего рассмотрения введем вспомогательную функцию Г*, вычисляющую по состоянию в автомате и последовательности асинхронных взаимодействий, множество состояний автомата, достижимых из данного по последовательности дуг, помеченных данной последовательностью взаимодействий. Формальное определение функции Г* следующее:
Г* ( v0, ( p1, p2, …, pn ) ) = 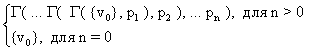 , где
, где
Г( V, p ) = 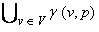 .
.
Лемма.
Для последовательности асинхронных взаимодействий ( p1, p2, …, pn ) существует путь ( e1, e2, …, en ) в автомате A, начинающийся в состоянии v0 и помеченный данными взаимодействиями, тогда и только тогда, когда Г* ( v0, ( p1, p2, …, pn ) ) ≠ Ø.
Доказательство.
Действительно, пусть существует путь v0 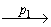 v1
v1 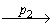 …
… 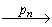 vn в автомате A, начинающийся в состоянии v0 и помеченный взаимодействиями ( p1, p2, …, pn ). Докажем индукцией по длине пути, что vn
vn в автомате A, начинающийся в состоянии v0 и помеченный взаимодействиями ( p1, p2, …, pn ). Докажем индукцией по длине пути, что vn  Г*( v0, ( p1, p2, …, pn ) ), а следовательно Г* ( v0, ( p1, p2, …, pn ) ) ≠ Ø.
Г*( v0, ( p1, p2, …, pn ) ), а следовательно Г* ( v0, ( p1, p2, …, pn ) ) ≠ Ø.
Базис индукции. (n = 1)
Итак, пусть v0 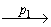 v1. Тогда v1
v1. Тогда v1  γ( v0, p1 )
γ( v0, p1 )  v1
v1  Г( {v0}, p1 ) = Г*( v0, ( p1 ) ).
Г( {v0}, p1 ) = Г*( v0, ( p1 ) ).
Шаг индукции.
Предположим, что мы доказали утверждение для путей длины n-1. Докажем его для n.
Пусть существует путь v0 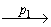 v1
v1 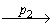 …
… 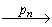 vn в автомате A, начинающийся в состоянии v0 и помеченный взаимодействиями ( p1, p2, …, pn ). Тогда по предположению индукции vn-1
vn в автомате A, начинающийся в состоянии v0 и помеченный взаимодействиями ( p1, p2, …, pn ). Тогда по предположению индукции vn-1  Г*( v0, ( p1, p2, …, pn-1 ) ). Но vn-1
Г*( v0, ( p1, p2, …, pn-1 ) ). Но vn-1 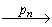 vn, то есть vn
vn, то есть vn  γ( vn-1, pn )
γ( vn-1, pn )  vn
vn  Г( Vn-1, pn ), где Vn-1 - любое множество, содержащее vn-1, в том числе Vn-1 = Г*( v0, ( p1, p2, …, pn-1 ) ). Следовательно vn
Г( Vn-1, pn ), где Vn-1 - любое множество, содержащее vn-1, в том числе Vn-1 = Г*( v0, ( p1, p2, …, pn-1 ) ). Следовательно vn  Г( Г*( v0, ( p1, p2, …, pn-1 ) ), pn ) = Г*( v0, ( p1, p2, …, pn ) ).
Г( Г*( v0, ( p1, p2, …, pn-1 ) ), pn ) = Г*( v0, ( p1, p2, …, pn ) ).
В обратную сторону.
Пусть Г*( v0, ( p1, p2, …, pn ) ) ≠ Ø. Докажем индукцией по n, что в автомате A существует путь v0 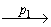 v1
v1 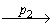 …
… 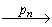 vn, начинающийся в состоянии v0 и помеченный взаимодействиями ( p1, p2, …, pn ).
vn, начинающийся в состоянии v0 и помеченный взаимодействиями ( p1, p2, …, pn ).
Базис индукции. (n = 1)
Пусть Г* ( v0, ( p1 ) ) ≠ Ø. Тогда существует v1  Г* ( v0, ( p1 ) ) = Г( {v0}, p1 ) = γ( v0, p1 ). То есть переход v0
Г* ( v0, ( p1 ) ) = Г( {v0}, p1 ) = γ( v0, p1 ). То есть переход v0 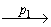 v1 принадлежит автомату A и является искомым путем.
v1 принадлежит автомату A и является искомым путем.
Шаг индукции.
Предположим, что мы доказали утверждение для n-1. Докажем его для n.
Пусть Г* ( v0, ( p1, p2, …, pn ) ) ≠ Ø.
Тогда  k
k  {1,…,n-1}
{1,…,n-1} 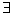 vk
vk  Г* ( v0, ( p1, p2, …, pk ) ): Г* ( vk, ( pk+1, pk+2, …, pn ) ) ≠ Ø.
Г* ( v0, ( p1, p2, …, pk ) ): Г* ( vk, ( pk+1, pk+2, …, pn ) ) ≠ Ø.
Предположим, что это не так.
То есть 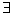 k
k  {1,…,n-1}
{1,…,n-1}  vk
vk  Г* ( v0, ( p1, p2, …, pk ) ) Г* ( vk, ( pk+1, pk+2, …, pn ) ) ≠ Ø.
Г* ( v0, ( p1, p2, …, pk ) ) Г* ( vk, ( pk+1, pk+2, …, pn ) ) ≠ Ø.
Тогда Г* ( v0, ( p1, p2, …, pn ) ) = Г( … Г( Г* ( v0, ( p1, p2, …, pk ) ), pk+1 ), … pn ) =
= 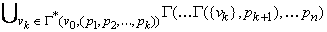 =
= 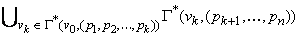 =
=
= 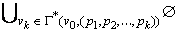 = Ø, что противоречит исходному предположению.
= Ø, что противоречит исходному предположению.
Данное утверждение верно и для k = 1. То есть найдется такое состояние v1  Г*( v0, ( p1 ) ), что Г*( v1, ( p2, p3, …, pn ) ) ≠ Ø. Следовательно, по предположению индукции в автомате A существует путь v1
Г*( v0, ( p1 ) ), что Г*( v1, ( p2, p3, …, pn ) ) ≠ Ø. Следовательно, по предположению индукции в автомате A существует путь v1 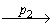 v2
v2 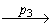 …
… 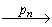 vn, начинающийся в состоянии v1 и помеченный взаимодействиями ( p2, p3, …, pn ).
vn, начинающийся в состоянии v1 и помеченный взаимодействиями ( p2, p3, …, pn ).
Так как v1  Г* ( v0, ( p1 ) ) = Г( {v0}, p1 ) = γ( v0, p1 ), то переход v0
Г* ( v0, ( p1 ) ) = Г( {v0}, p1 ) = γ( v0, p1 ), то переход v0 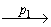 v1 также принадлежит автомату A. Следовательно в автомате A существует путь v0
v1 также принадлежит автомату A. Следовательно в автомате A существует путь v0  v1
v1  …
…  vn, начинающийся в состоянии v0 и помеченный взаимодействиями ( p1, p2, …, pn ).
vn, начинающийся в состоянии v0 и помеченный взаимодействиями ( p1, p2, …, pn ).
Как следует из леммы, проверка существования пути в автомате сводится к последовательному применению функции Г, вычислительная сложность которого сильно зависит от числа состояний, допускаемых моделью требований в качестве постсостояния перехода с заданными пресостоянием и асинхронным взаимодействием. В дальнейших оценках мы будем считать, что асинхронная модель требований допускает не более одного такого состояния, то есть модель является детерминированной.
Асинхронная модель требований A = ( V, X, Y, Z, E ) называется детерминированной, если для каждого состояния v  V и асинхронного взаимодействия p
V и асинхронного взаимодействия p  (X x Y)
(X x Y)  Z существует не более одного перехода ( u, x, u' )
Z существует не более одного перехода ( u, x, u' )  E, такого что u = v и x = p. Другими словами, в детерминированных моделях
E, такого что u = v и x = p. Другими словами, в детерминированных моделях  v, p | γ( v, p ) | ≤ 1.
v, p | γ( v, p ) | ≤ 1.
Для детерминированных моделей проверка существования пути, начинающегося в заданном состоянии v0 и помеченного заданной последовательностью взаимодействий ( p1, p2, …, pn ), в худшем случае сводится к n-кратному вычислению функции γ. Таким образом, сложность этой проверки оценивается сверху n-кратной сложностью вычисления функции γ.
Для оценки корректности асинхронной модели поведения такую проверку необходимо выполнить для каждой возможной линеаризации мультимножества асинхронных взаимодействий. А в худшем случае число линеаризаций составляет n!, где n - мощность множества P. То есть общая оценка сложности составляет n · n!.
Заметим, что многие линеаризации имеют общее начало. Этим свойством можно воспользоваться, чтобы не дублировать проверку существования путей, соответствующих общему началу линеаризаций.
Определим для множества P дерево возможных линеаризаций, как дерево, в котором
- из корня выходит n дуг, из вершин первого уровня - n-1 дуга, …, из вершин n-го уровня - 1 дуга и из вершин n+1-го уровня - ни одной дуги.
- каждая дуга помечена элементом из P,
- дуги, выходящие из вершины, путь к которой из корня дерева помечен последовательностью ( p1, p2, …, pk ), помечены элементами P, которые составляют множество Р \ { p1, p2, …, pk }.
Пример дерева возможных линеаризаций для P = { 1, 2, 3 } представлен на рисунке 11.
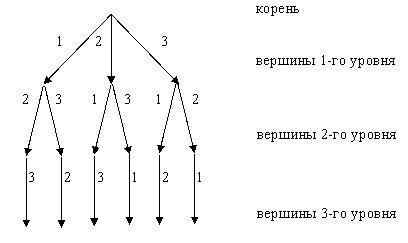
Рисунок 11. Дерево возможных линеаризаций для Р = { 1, 2, 3 }.
Заметим, что пути, ведущие из корня в листья, помечены последовательностями элементов из P, каждая из которых является линеаризацией множества P, а все вместе они образуют множество всех возможных линеаризаций.
Припишем к каждой вершине дерева возможных линеаризаций подмножество P, составленное из элементов { p1, p2, …, pk }, которыми помечен путь из корня дерева к данной вершине.
Деревом возможных линеаризаций частично-упорядоченного множества ( P,  ) мы будем называть дерево, полученное из дерева возможных линеаризаций множества P удалением всех поддеревьев, корню которых приписано множество не являющееся идеалом множества ( P,
) мы будем называть дерево, полученное из дерева возможных линеаризаций множества P удалением всех поддеревьев, корню которых приписано множество не являющееся идеалом множества ( P,  ). Дуга, ведущая в корень удаляемого поддерева, также удаляется.
). Дуга, ведущая в корень удаляемого поддерева, также удаляется.
Идеалами частично-упорядоченного множества ( P,  ) называются такие подмножества P, для которых выполнено условие: y
) называются такие подмножества P, для которых выполнено условие: y  I
I 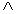 x
x  y
y  x
x  I.
I.
Лемма.
Пути из корня в листья дерева возможных линеаризаций частично-упорядоченного множества ( P,  ) помечены последовательностями элементов из P, составляющими множество всех возможных линеаризаций ( P,
) помечены последовательностями элементов из P, составляющими множество всех возможных линеаризаций ( P,  ).
).
Доказательство.
Покажем, что любой путь из корня в лист помечен последовательностью являющейся линеаризаций. Действительно, по построению дерева, любая такая последовательность является упорядочиванием всех элементов P. Покажем, что определяемый ею линейный порядок сохраняет исходный частичный порядок  .
.
Предположим, что это не так. То есть 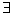 p1, p2
p1, p2  P: p1
P: p1  p2
p2 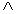 p2 < p1.
p2 < p1.
Из того, что p2 < p1 следует, что дуга, помеченная p2, встречается в пути раньше, чем дуга, помеченная p1. Следовательно, к вершине, в которую ведет дуга, помеченная p2, приписано множество, содержащее p2 и не содержащее p1. Такое множество не является идеалом, то есть рассматриваемые дуги не могут принадлежать дереву возможных линеаризаций. Противоречие показывает, что наше предположение не верно и любая последовательность на пути из корня в лист является линеаризаций.
Докажем, что для любой линеаризации ( P,  ) найдется путь в дереве возможных линеаризаций, помеченный последовательностью соответствующей данной линеаризации.
) найдется путь в дереве возможных линеаризаций, помеченный последовательностью соответствующей данной линеаризации.
Для этого мы рассмотрим путь в дереве возможных линеаризаций множества P, помеченный соответствующей последовательностью элементов ( p1, p2, …, pn ), и покажем, что этот путь будет присутствовать в дереве возможных линеаризаций частично-упорядоченного множества ( P,  ).
).
Предположим, что это не так и одна из вершин этого пути была удалена из дерева. Это могло произойти только в случае, когда данная вершина принадлежит поддереву, к корню которого приписано множество, не являющееся идеалом ( P,  ). Так как рассматриваемый путь ведет из корня в лист дерева, то корень любого поддерева, содержащего вершину из данного пути, также принадлежит этому пути. Следовательно, к одной из вершин рассматриваемого пути приписано множество, не являющееся идеалом ( P,
). Так как рассматриваемый путь ведет из корня в лист дерева, то корень любого поддерева, содержащего вершину из данного пути, также принадлежит этому пути. Следовательно, к одной из вершин рассматриваемого пути приписано множество, не являющееся идеалом ( P,  ).
).
Это множество состоит из элементов, приписанных к пути из корня дерева в эту вершину. Так как такой путь в дереве единственен, то он совпадает с началом пути ( p1, p2, …, pn ). Следовательно, 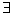 k: { p1, p2, …, pk } - не является идеалом ( P,
k: { p1, p2, …, pk } - не является идеалом ( P,  ). То есть существуют такие i и j, что pi
). То есть существуют такие i и j, что pi  { p1, p2, …, pk }
{ p1, p2, …, pk } 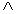 pj
pj  pi
pi 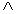 pj
pj 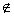 { p1, p2, …, pk }.
{ p1, p2, …, pk }.
Отсюда, i ≤ k < j 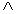 pj
pj  pi. Следовательно, последовательность ( p1, p2, …, pn ) не является линеаризацией, что противоречит нашему предположению.
pi. Следовательно, последовательность ( p1, p2, …, pn ) не является линеаризацией, что противоречит нашему предположению.
Если не дублировать проверку существования путей, соответствующих общему началу линеаризаций, то число необходимых вычислений функции γ будет совпадать с числом дуг в дереве возможных линеаризаций. Число дуг в дереве для множества размерностью n составляет:
n + n·(n-1) + … + n·(n-1)· … ·1 = 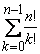 =
= 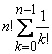 ≤
≤ 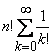 ≤ e·n!, где e - число Эйлера.
≤ e·n!, где e - число Эйлера.
Основной сложностью в реализации этого алгоритма является организация перебора возможных линеаризаций асинхронной модели поведения ( P,  ). Наиболее простой подход, основанный на переборе всех перестановок в лексикографическом порядке, требует O(n·n!) операций, так как для проверки того, является ли очередная перестановка линеаризацией, в этом случае требуется ∼n операций.
). Наиболее простой подход, основанный на переборе всех перестановок в лексикографическом порядке, требует O(n·n!) операций, так как для проверки того, является ли очередная перестановка линеаризацией, в этом случае требуется ∼n операций.
С другой стороны, существуют другие алгоритмы перебора перестановок, которые позволяют сократить затраты на проверку того, является ли очередная перестановка линеаризацией или нет. Но применение нетривиального перебора линеаризаций должно обеспечивать не только сложность O(n!), но и избегать перебора k! заведомо неподходящих перестановок, в тех случаях, когда известно, что (n-k)-ый элемент в какой-то перестановке нарушает условия линеаризации.
Алгоритм перебора линеаризаций, удовлетворяющий всем этим требованиям, был построен на основе алгоритма перебора перестановок 1.11, описанного в [29]. Этот алгоритм обеспечивает перебор перестановок таким образом, что каждая последующая перестановка отличается от предыдущей транспозицией одной пары элементов. В результате, проверка соответствия очередной перестановки условиям линеаризации требует в большинстве случаев константного времени. И в то же время, данный алгоритм позволяет избежать перебора k! заведомо неподходящих перестановок.
Алгоритм проверки корректности поведения, представленный ниже, основан на обходе дерева возможных линеаризаций в глубину. В нем используется следующая вспомогательная функция int B (int m , int i ), сложность вычисления которой ограничена константой:
int B(int m, int i)
{ if ((m%2 == 0) && (m > 2))
{if ( i < m-1 )
return i;
else
return m-2; }
else
return m-1; }
Сам алгоритм представлен далее.
Алгоритм проверки корректности поведения.
Входные данные.
Асинхронная модель поведения ( P,  ) задана:
) задана:
- массивом асинхронных взаимодействий P ( |P| = n );
- двухмерным массивом частичного порядка order[n,n]
- order[i,j] = 1, если P[i]
 P[j];
P[j];
- order[i,j] = 0, в противном случае.
Асинхронная модель требований A = ( V, X, Y, Z, E ) задана функцией возможных постсостояний γ : V x ( (X x Y)  Z )
Z )  2V .
2V .
Начальное состояние v0  V.
V.
Данные алгоритма.
bound : Nat[n] := { n, n-1, …, 2, 1 }
массив счетчиков числа точек ветвления дерева возможных линеаризаций.
perm : Nat[n] := { 0, 1, …, n-1 }
массив, хранящий текущую перестановку взаимодействий.
current : Nat := 0
индекс текущего элемента перестановки.
path : (V-set)[n+1] := { {v0}, Ø, …, Ø }
массив множеств состояний текущего пути в модели требований. Для детерминированных моделей требований этот массив может быть заменен на массив состояний V, так как все его элементы будут множествами с размерностью не более 1.
processed : Nat := 0
индекс наибольшего элемента пути, содержащего актуальное множество состояний модели требований.
order_failed : Bool := false
флаг, содержащий истинное значение только в том случае, когда текущая перестановка не является линеаризацией частичного порядка  .
.
current2 : Nat := 0
вспомогательная переменная для хранения индекса второго взаимодействий, участвовавшего в последней транспозиции.
tmp : Nat := 0
вспомогательная переменная.
j : Nat := 0
вспомогательная переменная.
Алгоритм.
- Алгоритм вычисляет является ли текущая перестановка perm линеаризацией частичного порядка
 , записывает результат в переменную order_failed и переходит к шагу 2, если текущая перестановка не противоречит частичному порядку
, записывает результат в переменную order_failed и переходит к шагу 2, если текущая перестановка не противоречит частичному порядку  , или к шагу 3 - в противном случае. При этом предполагается, что упорядочение P[perm[0]], …, P[perm[current]] не противоречит частичному порядку
, или к шагу 3 - в противном случае. При этом предполагается, что упорядочение P[perm[0]], …, P[perm[current]] не противоречит частичному порядку  и поэтому достаточно проверить элементы перестановки, начиная с current.
и поэтому достаточно проверить элементы перестановки, начиная с current.
for(;current<n-1;current++)
{for(j=current+1;j<n;j++)
{if (order[perm[j],perm[current]])
{order_failed = true;
goto 3; } } }
order_failed = false;
- Алгоритм строит пути в модели требований, соответствующие последовательности взаимодействий в текущей перестановке, заполняя массив path. При этом предполагается, что начальные отрезки пути path[0], …, path[processed] уже построены ранее. Если на одном из шагов множество состояний модели требований оказывается пустым, то алгоритм переходит к шагу problem, установив значение переменной current равное индексу элемента перестановки для которого было получено пустое множество. Если же path[n] ≠ Ø, то алгоритм завершает свою работу с положительным вердиктом. Найдена линеаризация ( P[perm[0]], P[perm[1]],…, P[perm[n-1]] ), для которой множество Г*( v0, ( P[perm[0]], P[perm[1]], …, P[perm[n-1]] ) ) = path[n] не пусто.
for(;processed<n;processed++)
{path[processed+1] = Ø;
foreach v : V in path[processed]
path[processed+1] = path[processed+1]
 γ( v, P[perm[processed]] );
if (path[processed+1] == Ø)
{current = processed;
for(j=current+1;j<n;j++)
bound[j] = n-j;
goto 3; } }
КОНЕЦ (асинхронная модель поведения является корректной
относительно данной асинхронной модели требований)
γ( v, P[perm[processed]] );
if (path[processed+1] == Ø)
{current = processed;
for(j=current+1;j<n;j++)
bound[j] = n-j;
goto 3; } }
КОНЕЦ (асинхронная модель поведения является корректной
относительно данной асинхронной модели требований)
- Если индекс текущего элемента перестановки больше либо равен n-2 или , то алгоритм переходит к шагу 9.
if ((current ≥ n-2) || (bound[current] == 1))
goto 9;
- Если индекс текущего элемента перестановки является нечетным при обратной нумерации элементов перестановки [n-1
 0, …, 0
0, …, 0  n-1], то алгоритм переходит к шагу 7.
n-1], то алгоритм переходит к шагу 7.
if ((n-current) % 2 == 0)
goto 7;
- Алгоритм осуществляет циклический сдвиг хвоста перестановки на единицу
perm[current+2]  perm[current+1]
…
perm[n-1]
perm[current+1]
…
perm[n-1]  perm[n-2]
perm[current+1]
perm[n-2]
perm[current+1]  perm[n-1]
tmp = perm[current+1];
for(j=current+1;j<n-1;j++)
perm[j] = perm[j+1];
perm[n-1] = tmp;
perm[n-1]
tmp = perm[current+1];
for(j=current+1;j<n-1;j++)
perm[j] = perm[j+1];
perm[n-1] = tmp;
- Если предыдущая перестановка не противоречила частичному порядку
 , то алгоритм вычисляет не противоречит ли новая перестановка этому порядку, записывает результат в переменную order_failed и переходит к шагу 9.
, то алгоритм вычисляет не противоречит ли новая перестановка этому порядку, записывает результат в переменную order_failed и переходит к шагу 9.
if (!order_failed)
{for(j=current+1;j<n-1;j++)
{if (order[perm[n-1],perm[j]])
{order_failed = true;
break; } } }
goto 9;
- Алгоритм осуществляет транспозицию элементов перестановки с индексами current+1 и current+2.
tmp = perm[current+1];
perm[current+1] = perm[current+2];
perm[current+2] = tmp;
- Если предыдущая перестановка не противоречила частичному порядку
 , то алгоритм вычисляет не противоречит ли новая перестановка этому порядку и записывает результат в переменную order_failed.
, то алгоритм вычисляет не противоречит ли новая перестановка этому порядку и записывает результат в переменную order_failed.
if (!order_failed)
{if (order[perm[current+2],perm[current+1]])
order_failed = true; }
- Если текущий счетчик числа точек ветвления равен 1, то алгоритм переходит к шагу 14.
if (bound[current] == 1)
goto 14;
- Алгоритм осуществляет транспозицию элементов перестановки с индексами current и n-B(n-current,n-current-bound[current]+1), сохраняя индекс второго элемента в переменной current2.
current2 = n-B(n-current,n-current-bound[current]+1);
tmp = perm[current];
perm[current] = perm[current2];
perm[current2] = tmp;
- Алгоритм уменьшает текущий счетчик числа точек ветвления на единицу.
bound[current]--;
- Если предыдущая перестановка противоречила частичному порядку
 ;, то алгоритм переходит к шагу 1.
;, то алгоритм переходит к шагу 1.
if (order_failed)
goto 1;
- В противном случае алгоритм вычисляет, не противоречит ли новая перестановка частичному порядку
 , записывает результат в переменную order_failed и переходит к шагу 2, если текущая перестановка не противоречит частичному порядку
, записывает результат в переменную order_failed и переходит к шагу 2, если текущая перестановка не противоречит частичному порядку  , или к шагу 3 - в противном случае. В последнем случае алгоритм устанавливает значение переменной current равное наименьшему индексу элемента перестановки, для которого нарушается условие линеаризации.
, или к шагу 3 - в противном случае. В последнем случае алгоритм устанавливает значение переменной current равное наименьшему индексу элемента перестановки, для которого нарушается условие линеаризации.
for(j=current+1;j<=current2;j++)
{if (order[perm[j],perm[current]])
{order_failed = true;
goto 3; } }
for(j=current+1;j<current2;j++)
{if (order[perm[current2],perm[j]])
{order_failed = true;
current = j;
goto 3; } }
goto 2;
- Если индекс текущего элемента перестановки равен 0, то алгоритм завершает свою работу с отрицательным вердиктом.
if (current == 0)
КОНЕЦ (асинхронная модель поведения является
не корректной относительно данной асинхронной
модели требований)
- В противном случае алгоритм переинициализирует текущий счетчик числа точек ветвления и уменьшает индекс текущего элемента перестановки на единицу.
bound[current] = n-current;
current--;
- Если индекс текущего элемента перестановки оказался меньше индекса наибольшего элемента пути, содержащего актуальное множество состояний модели требований, то значение последнего устанавливается равным значению первого.
if (current < processed)
processed = current;
- Алгоритм переходит к шагу 9.
goto 9;
Доказательство корректности данного алгоритма представлено в [30].
Частичный порядок  модели поведения рассматривается в алгоритме в виде двухмерной матрицы n x n, содержащей значение 1 для пар принадлежащих частичному порядку и 0 - в противном случае. Для построения этой матрицы на основе моделей каналов и временных меток можно использовать алгоритм построения транзитивного замыкания Уоршала, который требует O(n3 ) операций [29]. Существуют также алгоритмы построения транзитивного замыкания с лучшей оценкой (например, O(nlog 7·log n)), однако они имеют преимущества только при очень больших значениях n.
модели поведения рассматривается в алгоритме в виде двухмерной матрицы n x n, содержащей значение 1 для пар принадлежащих частичному порядку и 0 - в противном случае. Для построения этой матрицы на основе моделей каналов и временных меток можно использовать алгоритм построения транзитивного замыкания Уоршала, который требует O(n3 ) операций [29]. Существуют также алгоритмы построения транзитивного замыкания с лучшей оценкой (например, O(nlog 7·log n)), однако они имеют преимущества только при очень больших значениях n.
Обратим внимание на тот факт, что оценка сложности алгоритма O(n!) получена для класса детерминированных моделей поведения, для недетерминированных моделей сложность становится еще больше. Но даже при использовании детерминированных моделей требования применимость алгоритма сильно ограничена: при числе взаимодействий, превышающем несколько десятков время работы становится неприемлемо большим. Поэтому при применении рассматриваемого метода необходимо учитывать имеющиеся ограничения на размерность модели поведения, участвующей в задаче оценки корректности.
Требования к полноте набора асинхронных реакций
Асинхронная модель требований позволяет оценить являются ли корректными взаимодействия с целевой системой, произошедшие в процессе тестирования. В то же время, для асинхронных систем существуют требования другого вида, которые также необходимо проверять. Это требования к полноте набора асинхронных реакций.
Например, рассмотрим ситуацию, когда в ответ на некоторое воздействие целевая система должна выдать две асинхронных реакции, но выдает только одну. В этом случае, асинхронная модель поведения всегда будет удовлетворять модели требований, так как все взаимодействия по отдельности являются корректными. В то же время, набор всех взаимодействий с точки зрения пользователя является некорректным, так как в нем отсутствует часть необходимых асинхронных реакций.
Такого рода несоответствие между формальной оценкой корректности поведения и ожиданиями пользователя происходит по двум причинам:
- из-за отсутствия в асинхронных моделях требований ограничений на момент, когда должна появиться ожидаемая асинхронная реакция;
- из-за отсутствия в асинхронных моделях поведения явного подтверждения того факта, что временная граница получения реакции была пройдена.
В результате этого, при отсутствии одной из ожидаемых асинхронных реакций оценка корректности дает положительный вердикт, так как считается, что данная реакция еще может быть получена позднее.
Для выявления такого рода некорректностей можно предложить следующий подход. К множеству асинхронных реакций асинхронного интерфейса ( X, Y, Z ) добавляется вспомогательная асинхронная реакция done, семантика которой заключается в отражении того факта, что время, отведенное на получение асинхронных реакций, вышло. Соответственно, в асинхронную спецификацию добавляется спецификация псевдо интерфейсной операции Specdone, описывающая корректные переходы модели требований, помеченные реакцией done. Эти переходы предлагается интерпретировать следующим образом. Если из данного состояния модели требований v  V существует переход, помеченный асинхронной реакцией z
V существует переход, помеченный асинхронной реакцией z  Z, то
Z, то
- если из этого состояния существует переход, помеченный реакцией done, то мы будем говорить, что асинхронная реакция z является опциональной в состоянии v, то есть целевая система может выдать данную реакцию, а может и не выдать.
- если из этого состояния не существует перехода, помеченного реакцией done, то мы будем говорить, что асинхронная реакция z является обязательной в состоянии v, то есть целевая система обязана выдать данную реакцию.
Для использования псевдо реакции done тестовая система должна при завершении тестирования выждать время, необходимое для получения всех асинхронных реакций, и добавить в построенную асинхронную модель поведения псевдо реакцию done таким образом, чтобы согласно частичному порядку эта псевдо реакция была больше всех остальных взаимодействий. При таком подходе удается разрешить рассмотренную выше проблему с проверкой неполноты набора асинхронных реакций.
Заметим, что это возможно только тогда, когда время получения всех асинхронных реакций ограничено, так как в противном случае появление псевдо реакции done в асинхронной модели поведения становится невозможным.
Данное ограничение может быть ослаблено, до требования ограниченности времени получения всех обязательных асинхронных реакций, где под обязательными реакциями понимаются реакции, которые являются обязательными хотя бы в одном состоянии модели требований.
Для описания более детальных ограничений, таких как требования вида "асинхронная реакция должна появиться не позже, чем" и " асинхронная реакция должна появиться не раньше, чем" необходимо отражение выделенных моментов времени как в модели требований, так и в модели поведения. Для решения этой задачи можно предложить два подхода.
Первый подход предполагает введение псевдо асинхронных реакций, предназначенных для симулирования наступления временных границ (нижний или верхней) для каждой конкретной асинхронной реакции. В модели требований такие псевдо реакции должны использоваться для описания соответствующих ограничений на момент появления реакции, а в модели поведения они должны отражать соответствующие моменты времени.
Второй подход основывается на использовании модели временных меток. Для этого к каждому асинхронному взаимодействию приписывается временной интервал, то есть в асинхронном интерфейсе целевой системы множества Y и Z заменяются на Y x TI(TM) и Z x TI(TM) соответственно. В этом случае, в спецификациях интерфейсных операций временные метки учитываются при описании требований ко времени получения реакций, посредством сохранения в модельном состоянии информации о времени осуществления соответствующих асинхронных воздействий. Во втором подходе также может потребоваться использование множества псевдо асинхронных реакций { done } x TI(TM) для отражения момента завершения сбора асинхронных реакций.
Следует также отметить, что работа с временными свойствами обладает целым рядом проблем, связанных со сложностью отслеживания временных характеристик работы целевой системы. Поэтому такая работа должна проводиться с учетом возможных неточностей в измерении. Для этого основным инструментом работы со временем сделан временной интервал, описывающий не единственный момент во времени, а целый интервал, ограниченный минимальной и максимальной временными метками.
Рассмотренные методы организации проверки дополнительных требований к полноте набора асинхронных реакций и времени их появления построены на использовании ранее определенных моделей поведения и требований. Изменения касались только технологии использования этих моделей. Поэтому для реализации дополнительных проверок никаких изменений в моделях поведения и требований и алгоритмах работы с ними не требуется.
Модели требований и поведения в унифицированной архитектуре асинхронного теста
Компонент тестовой системы, ответственный за взаимодействие с целевой системой и построение модели ее поведения, мы, как и ранее, будем называть медиатором. Компонент, решающий задачу оценки корректности поведения тестируемой системы в ходе работы теста, мы будем называть оракулом. Рассмотрим более детально их внутреннее устройство и способ взаимосвязи.
Отличия в архитектуре тестовой системы для асинхронных систем диктуются основными особенностями этих систем:
- наличием взаимодействий, инициируемых целевой системой;
- возможностью одновременного участия целевой системы в нескольких взаимодействиях.
При тестировании асинхронных систем их поведение уже не может рассматриваться как набор отдельных, не связанных между собой взаимодействий. Между этими взаимодействиями существуют зависимости, которые необходимо учитывать и при построении модели поведения, и при оценке ее корректности.
Отсюда появляется необходимость в компоненте, в котором будет собираться информация обо всех взаимодействиях с тестируемой системой и зависимостях между ними. Этот компонент называется регистратором взаимодействий. Информация, собираемая в нем, представляет собой модель поведения целевой системы в процессе работы теста. В дальнейшем она будет использоваться для оценки корректности поведения.
Информация о взаимодействиях попадает в регистратор взаимодействий двумя путями. Взаимодействия, инициируемые тестовой системой, регистрируются медиаторами воздействий. Помимо регистрации взаимодействий эти медиаторы ответственны за осуществление воздействия на тестируемую систему. Работа медиатора воздействия строится по следующему алгоритму. Получив указание подать стимул x  X, медиатор преобразует его в соответствующее воздействие на целевую систему и осуществляет его. Затем медиатор воздействия получает ответную реакцию целевой системы, преобразуют ее в модельное представление y
X, медиатор преобразует его в соответствующее воздействие на целевую систему и осуществляет его. Затем медиатор воздействия получает ответную реакцию целевой системы, преобразуют ее в модельное представление y  Y и регистрирует взаимодействие ( x, y )
Y и регистрирует взаимодействие ( x, y )  X x Y в регистраторе взаимодействий.
X x Y в регистраторе взаимодействий.
Взаимодействия, инициируемые целевой системой, регистрируются кетчерами, задачей которых является получении информации обо всех таких взаимодействиях, преобразование каждого взаимодействия в модельное представление z  Z и регистрация его в регистраторе взаимодействий.
Z и регистрация его в регистраторе взаимодействий.
Для передачи тестовой системе известной информации о последовательности, в которой происходили взаимодействия, используются модель каналов и модель временных меток. Модель каналов строится следующим образом. При регистрации каждого взаимодействия указывается идентификатор канала, к которому оно относится. При этом считается, что все взаимодействия, зарегистрированные с одинаковым идентификатором канала, образуют один канал. Линейный порядок в рамках этого канала определяется последовательностью регистрации взаимодействий: если из двух взаимодействий, зарегистрированных с одним идентификатором канала, одно было зарегистрировано раньше другого, то первое меньше второго в линейном порядке соответствующего канала.
Модель временных меток определяется похожим способом. При регистрации каждого взаимодействия ему приписывается временной интервал. Кроме того, в процессе работы теста имеющаяся информация о взаимном порядке временных меток, принадлежащих различным системам координат, должна быть передана регистратору взаимодействий. Таким образом, в регистраторе взаимодействий будет собрано все необходимое для определения модели временных меток.
У медиатора, использовавшегося для тестирования синхронных систем, была еще одна важная функция - синхронизация модельного состояния с состоянием реализации. При тестировании с открытым состоянием синхронизация осуществлялась посредством чтения внутреннего состояния целевой системы и преобразования его в модельное представление. При тестировании с закрытым состоянием синхронизация проводилась путем вычисления модельного состояния, удовлетворяющего модели требований, с учетом дополнительных знаний медиатора о деталях поведения тестируемой реализации.
Тестирование асинхронных систем, как правило, можно проводить только с закрытым состоянием, так как из-за асинхронности поведения не представляется возможным прочитать состояние целевой системы, в котором она находилась после определенного взаимодействия. Поэтому при тестировании асинхронных систем модельное состояние не рассматривается как часть модели поведения целевой системы. Оно используется только в модели требований для определения корректности поведения.
В алгоритме оценки корректности поведения функция γ описывает множество допустимых модельных состояний после данного взаимодействия при заданном начальном состоянии системы. Модель требований может допускать большое количество таких состояний, абстрагируясь от деталей реализации описываемых требований. Анализ всех этих состояний может требовать большого количества ресурсов. В то же время, при тестировании конкретной целевой системы может быть известно о деталях поведения данной реализации, на основе которых можно ограничить множество допустимых модельных состояний только теми состояниями, которые будут соответствовать корректному поведению данной реализации. Так как такое ограничение является реализационнозависимым, то оно описывается в медиаторе, а именно в специальном компоненте медиатора, называемом медиатором состояния. Подробнее, назначение медиатора состояния будет рассмотрено при обсуждении работы оракула.
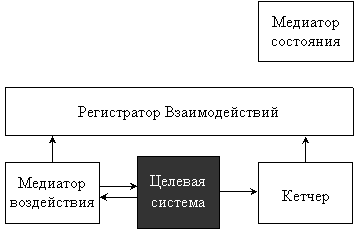
Рисунок 12. Медиатор в универсальной архитектуре асинхронного теста
Устройство медиатора, предназначенного для тестирования асинхронных систем, представлено на рисунке 12. Как и ранее, стрелками здесь обозначены направления передачи данных между компонентами тестовой системы.
Оракул решает задачу оценки корректности поведения тестируемой системы в ходе работы теста. Алгоритм решения этой задачи был представлен в предыдущем разделе. Он учитывает в своей работе все имевшие место взаимодействия с тестируемой системой и связи между ними. Поэтому компонент оракула, реализующий этот алгоритм, мы будем называть гипероракулом. Гипероракул получает от регистратора взаимодействий информацию обо всех взаимодействиях, зарегистрированных в процессе работы теста, и дальше действует согласно алгоритму оценки корректности поведения.
Алгоритм оценки корректности поведения предполагает, что модель требований задана посредством функции γ : V x ( (X x Y)  Z )
Z )  2V , однако в действительности модель поведения описывается асинхронной спецификацией { SpecSi | i = 1, …, k; k > 0 }
2V , однако в действительности модель поведения описывается асинхронной спецификацией { SpecSi | i = 1, …, k; k > 0 }  { SpecRj | j = 1, …, m; m ≥ 0 }. Поэтому необходимо рассмотреть каким образом гипероракул организует вычисление функции γ.
{ SpecRj | j = 1, …, m; m ≥ 0 }. Поэтому необходимо рассмотреть каким образом гипероракул организует вычисление функции γ.
Вычисление функции γ на основе асинхронной спецификации является задачей эквивалентной решению системы уравнений произвольной сложности. И так как автоматически решить эту задачу не представляется возможным, то тестовая система полагается в этом случае на подсказку пользователя. В качестве такой подсказки предлагается использовать функцию γ' : V x ( (X x Y)  Z )
Z )  2V , которая вычисляет конечное множество состояний, включающее в себя все потенциальные элементы γ( v, p ):
2V , которая вычисляет конечное множество состояний, включающее в себя все потенциальные элементы γ( v, p ):
 v
v  V
V  p
p  ( (X x Y)
( (X x Y)  Z ) |γ'( v, p )| < ∞
Z ) |γ'( v, p )| < ∞  γ( v, p ))
γ( v, p ))  γ'( v, p )
γ'( v, p )
Обладая такой подсказкой, тестовая система получает возможность рассмотреть конечное множество потенциальных решений и вычислить искомое множество γ( v, p ), отсеяв элементы γ'( v, p ), не удовлетворяющие заданной асинхронной спецификации.
Заметим, что определение функции γ' очень близко к описанию ограничения на множество допустимых модельных состояний, осуществляемое в медиаторе состояния. Действительно, в медиаторе состояния в целях оптимизации предполагается ограничить множество допустимых состояний, что соответствует определению дополнительной функции γ'' : V x ( (X x Y)  Z )
Z )  2V , учитывающей детали поведения тестируемой реализации и вычисляющей подмножество множества γ( v, p ):
2V , учитывающей детали поведения тестируемой реализации и вычисляющей подмножество множества γ( v, p ):
 v
v  V
V  p
p  ( (X x Y)
( (X x Y)  Z ) γ''( v, p )
Z ) γ''( v, p )  γ( v, p )
γ( v, p )
Предполагается, что подмножество γ''( v, p ) включает в себя не все допустимые модельные состояния, а только те, которые являются корректными, учитывая детали поведения тестируемой реализации. Другими словами, использование функции γ'' позволяет уточнять абстрактную модель требований дополнительными требованиями для конкретной реализации.
В унифицированной архитектуре асинхронного теста предлагается совместить определения уточнения требований и подсказки путем описания в медиаторе состояния функции γ* : V x ( (X x Y)  Z )
Z )  2V , результатом которой является конечное множество состояний. Это множество может быть шире множества допустимых состояний, вычисленных γ'' с учетом дополнительных требований. Но только за счет состояний, не удовлетворяющих исходной модели требований.
2V , результатом которой является конечное множество состояний. Это множество может быть шире множества допустимых состояний, вычисленных γ'' с учетом дополнительных требований. Но только за счет состояний, не удовлетворяющих исходной модели требований.
 v
v  V
V  p
p  ( (X x Y)
( (X x Y)  Z )
Z )
γ''( v, p )  γ*( v, p )
γ*( v, p )  γ'( v, p )
γ'( v, p )  γ*( v, p )
γ*( v, p )  γ( v, p ) = γ''( v, p )
γ( v, p ) = γ''( v, p )
В простейшем случае, при отсутствии уточнения требований, функция γ* совпадает с функцией подсказки γ'.
Далее мы будем считать, что размерность множества γ*( v, p ) не превышает 1. Это требование является ограничением на область применимости архитектуры. Заметим, что данное ограничение выполняется для всех детерминированных моделей требований и, кроме того, оно выполняется для недетерминированных моделей требований, если требования к тестируемой реализации могут быть уточнены до достижения детерминированности.
Итак, гипероракул вычисляет вместо функции γ ее модификацию γ''( v, p ), и это вычисление происходит следующим образом:
- Гипероракул устанавливает модельное состояние равным v.
- Гипероракул вызывает оракул воздействия для взаимодействия p.
- Оракул воздействия вычисляет предусловие взаимодействия p: preS
 R (v,p).
R (v,p).
- Если нарушено предусловие интерфейсной операции-стимула (p
 X x Y), то тестовая система завершает свою работу 7.
X x Y), то тестовая система завершает свою работу 7.
- Если нарушено предусловие интерфейсной операции-реакции (p
 Z), то оракул воздействия возвращает отрицательный вердикт и результатом вычисления γ'' является пустое множество.
Z), то оракул воздействия возвращает отрицательный вердикт и результатом вычисления γ'' является пустое множество.
- Оракул воздействия сохраняет все необходимые части текущего модельного состояния v и вызывает медиатор состояния для взаимодействия p.
- Медиатор состояния читает текущее модельное состояние v и вычисляет γ*( v, p ).
- Если γ*( v, p ) пусто, то медиатор состояния возвращает отрицательный вердикт и результатом вычисления γ'' является пустое множество.
- В противном случае, множество γ*( v, p ) состоит из одного элемента v'. Тогда медиатор состояния записывает v' в модельное состояние и возвращает управление оракулу воздействия с положительным вердиктом.
- Оракул воздействия вычисляет постусловие взаимодействия p для сохраненного состояния v и текущего модельного состояния v': postS
 R( v, p, v' ).
R( v, p, v' ).
- Если постусловие нарушено, то оракул воздействия возвращает отрицательный вердикт и результатом вычисления γ'' является пустое множество
- В противном случае оракул воздействия возвращает положительный вердикт и результатом вычисления γ'' является множество { v' }, где v' - текущее значение модельного состояния.
Диаграмма последовательности взаимодействия, описывающая успешное вычисление функции γ'' представлена на рисунке 13.
Такая архитектура вычисления функции γ'' позволяет без изменений использовать оракулы воздействий для тестирования как синхронных, так и асинхронных систем.
Схема работы асинхронного теста по оценке корректности поведения целевой системы представлена на рисунке 14. Как и ранее, стрелками здесь обозначены направления передачи данных между компонентами тестовой системы.
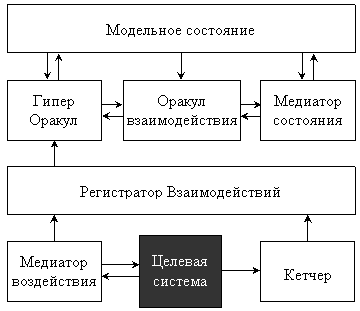
Рисунок 14. Схема работы асинхронного теста по оценке корректности поведения целевой системы