2004 г
Назад Оглавление Вперёд
5. Элементы
теории
перевода
До сих
пор мы
рассматривали
процесс
синтаксического
анализа
только как
процесс
анализа
допустимости
входной
цепочки.
Однако, в
компиляторе
синтаксический
анализ
служит
основой
еще одного
важного
шага -
построения
дерева
синтаксического
анализа. В
примерах 4.3 и 4.8
предыдущей
главы в
процессе
синтаксического
анализа в
качестве
выхода
выдавалась
последовательность
примененных
правил,
на основе
которой и
может быть
построено
дерево.
Построение
дерева
синтаксического
анализа
является
простейшим
частным
случаем
перевода -
процесса
преобразования
некоторой
входной
цепочки в
некоторую
выходную.
Определение. Пусть T -
входной
алфавит, а  - выходной
алфавит.
Переводом
(или
трансляцией)
с языка L1
- выходной
алфавит.
Переводом
(или
трансляцией)
с языка L1  T*
на язык L2
T*
на язык L2 
 *
называется
отображение
*
называется
отображение
 : L1
: L1  L2. Если y =
L2. Если y =  (x), то
цепочка y
называется
выходом для
цепочки
x.
(x), то
цепочка y
называется
выходом для
цепочки
x.
Мы рассмотрим
несколько
формализмов
для
определения
переводов:
преобразователи
с магазинной
памятью,
схемы
синтаксически
управляемого
перевода и
атрибутные
грамматики.
5.1 Преобразователи
с магазинной
памятью
Рассмотрим
важный
класс
абстрактных
устройств,
называемых
преобразователями
с магазинной
памятью. Эти
преобразователи
получаются
из автоматов
с магазинной
памятью,
если к ним
добавить
выход и
позволить
на каждом
шаге
выдавать
выходную
цепочку.
Преобразователем
с магазинной
памятью
(МП-преобразователем)
называется
восьмерка
P = (Q, T, 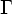 ,
,  , D, q0, Z0, F), где все
символы
имеют тот
же смысл,
что и в
определении
МП-автомата,
за исключением
того, что
, D, q0, Z0, F), где все
символы
имеют тот
же смысл,
что и в
определении
МП-автомата,
за исключением
того, что  -
конечный
выходной
алфавит, а D -
отображение
множества QЧ(T
-
конечный
выходной
алфавит, а D -
отображение
множества QЧ(T {e})Ч
{e})Ч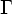 в множество
конечных
подмножеств
множества
Q Ч
в множество
конечных
подмножеств
множества
Q Ч 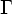 *Ч
*Ч  *.
*.
Определим
конфигурацию
преобразователя
P как
четверку
(q, x, u, y), где q  Q -
состояние,
x
Q -
состояние,
x  T* - цепочка
на входной
ленте, u
T* - цепочка
на входной
ленте, u 
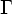 * -
содержимое
магазина, y
* -
содержимое
магазина, y 
 * -
цепочка на
выходной
ленте,
выданная
вплоть до
настоящего
момента.
* -
цепочка на
выходной
ленте,
выданная
вплоть до
настоящего
момента.
Если
множество
D(q, a, Z) содержит
элемент (r, u, z),
то будем
писать
(q, ax, Zw, y)  (r, x, uw, yz) для
любых x
(r, x, uw, yz) для
любых x  T*, w
T*, w 
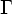 * и y
* и y 
 *.
Рефлексивно-транзитивное
замыкание
отношения
*.
Рефлексивно-транзитивное
замыкание
отношения
 будем
обозначать
будем
обозначать
 *.
*.
Цепочку y
назовем
выходом
для x, если
(q0, x, Z0, e)  *(q, e, u, y) для
некоторых q
*(q, e, u, y) для
некоторых q  F
и u
F
и u 
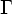 *. Переводом
(или
трансляцией),
определяемым
МП-преобразователем
P (обозначается
*. Переводом
(или
трансляцией),
определяемым
МП-преобразователем
P (обозначается
 (P)), назовем
множество
(P)), назовем
множество

Будем
говорить,
что
МП-преобразователь
P является
детерминированным
(ДМП-преобразователем),
если
выполняются
следующие
условия:
- для всех
q
 Q, a
Q, a  T
T {e} и Z
{e} и Z 
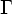 множество
D(q, a, Z) содержит
не более
одного элемента,
множество
D(q, a, Z) содержит
не более
одного элемента,
- если D(q, e, Z)
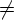
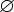 ,
то D(q, a, Z) =
,
то D(q, a, Z) = 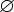 для
всех a
для
всех a  T.
T.
Пример 5.1. Рассмотрим
перевод  ,
отображающий
каждую
цепочку
x
,
отображающий
каждую
цепочку
x  {a, b}*$, в которой
число
вхождений
символа a
равно числу
вхождений
символа b, в
цепочку y = (ab)n,
где n - число
вхождений
a или b в
цепочку x.
Например,
{a, b}*$, в которой
число
вхождений
символа a
равно числу
вхождений
символа b, в
цепочку y = (ab)n,
где n - число
вхождений
a или b в
цепочку x.
Например,
 (abbaab$) = ababab.
(abbaab$) = ababab.
Этот перевод
может быть
реализован
ДМП-преобразователем
P = ({q0, qf}, {a, b, $}, {Z, a, b}, {a, b}, D, q0, Z, {qf}) c
функцией
переходов:
D(q0, X, Z) = {(q0, XZ, e)}, X  {a, b},
{a, b},
D(q0, $, Z) = {(qf, Z, e)},
D(q0, X, X) = {(q0, XX, e)}, X  {a, b},
{a, b},
D(q0, X, Y ) = {(q0, e, ab)}, X  {a, b}, Y
{a, b}, Y  {a, b}, X
{a, b}, X Y .
Y .
5.2 Синтаксически
управляемый
перевод
Другим
формализмом,
используемым
для
определения
переводов,
является
схема
синтаксически
управляемого
перевода.
Фактически,
такая
схема
представляет
собой
КС-грамматику,
в которой
к каждому
правилу
добавлен
элемент
перевода.
Всякий
раз, когда
правило
участвует
в выводе
входной
цепочки,
с помощью
элемента
перевода
вычисляется
часть
выходной
цепочки,
соответствующая
части
входной
цепочки,
порожденной
этим
правилом.
5.2.1 Схемы
синтаксически
управляемого
перевода
Определение. Cхемой
синтаксически
управляемого
перевода (или
трансляции,
сокращенно:
СУ-схемой)
называется
пятерка
Tr = (N, T,  , R, S), где
, R, S), где
- N - конечное
множество
нетерминальных
символов;
- T - конечный
входной
алфавит;
 - конечный
выходной
алфавит;
- конечный
выходной
алфавит;
- R - конечное
множество
правил перевода
вида
 где u
где u  (N
(N T)*, v
T)*, v  (N
(N
 )* и
вхождения
нетерминалов
в цепочку
v образуют
перестановку
вхождений
нетерминалов
в цепочку u,
так что каждому
вхождению
нетерминала
B в цепочку
u соответствует
некоторое
вхождение
этого же
нетерминала
в цепочку
v; если нетерминал
B встречается
более одного
раза, для
указания
соответствия
используются
верхние
целочисленные
индексы;
)* и
вхождения
нетерминалов
в цепочку
v образуют
перестановку
вхождений
нетерминалов
в цепочку u,
так что каждому
вхождению
нетерминала
B в цепочку
u соответствует
некоторое
вхождение
этого же
нетерминала
в цепочку
v; если нетерминал
B встречается
более одного
раза, для
указания
соответствия
используются
верхние
целочисленные
индексы;
- S - начальный
символ, выделенный
нетерминал
из N.
Определим
выводимую
пару в схеме
Tr следующим
образом:
- (S, S) - выводимая
пара, в которой
символы
S соответствуют
друг другу;
- если (xAy, x'Ay') - выводимая
пара, в цепочках
которой
вхождения
A соответствуют
друг другу,
и A
 u, v - правило
из R, то (xuy, x'vy') -
выводимая
пара. Для
обозначения
такого вывода
одной пары
из другой
будем пользоваться
обозначением
u, v - правило
из R, то (xuy, x'vy') -
выводимая
пара. Для
обозначения
такого вывода
одной пары
из другой
будем пользоваться
обозначением
 : (xAy, x'Ay')
: (xAy, x'Ay')  (xuy, x'vy'). Рефлексивно-транзитивное
замыкание
отношение
(xuy, x'vy'). Рефлексивно-транзитивное
замыкание
отношение
 обозначим
обозначим
 *.
*.
Переводом  (Tr),
определяемым
СУ-схемой Tr,
назовем
множество
пар
(Tr),
определяемым
СУ-схемой Tr,
назовем
множество
пар

Если через P
обозначить
множество
входных
правил
вывода
всех правил
перевода,
то G = (N, T, P, S) будет
входной
грамматикой
для Tr.
СУ-схема Tr = (N, T,  , R, S)
называется
простой,
если для
каждого
правила A
, R, S)
называется
простой,
если для
каждого
правила A  u, v из R
соответствующие
друг другу
вхождения
нетерминалов
встречаются
в u и v в одном
и том же
порядке.
u, v из R
соответствующие
друг другу
вхождения
нетерминалов
встречаются
в u и v в одном
и том же
порядке.
Перевод,
определяемый
простой
СУ-схемой,
называется
простым
синтаксически
управляемым
переводом
(простым
СУ-переводом).
Пример 5.2. Перевод
арифметических
выражений
в ПОЛИЗ
(польскую
инверсную
запись) можно
осуществить
простой
СУ-схемой с
правилами
| E  E + T, | ET+ |
| E  T, | T |
| T  T * F, | TF+ |
| T  F, | F |
| F  id, | id |
| F  (E), | E |
|
Найдем
выход схемы
для входа
id*(id+id). Нетрудно
видеть, что
существует
последовательность
шагов вывода
(E, E)  (T, T)
(T, T)  (T *F, TF*)
(T *F, TF*)  (F *F, FF*)
(F *F, FF*)  (id*F, id F*)
(id*F, id F*)  (id* (E), id E*)
(id* (E), id E*)  (id * (E + T), id E T + *)
(id * (E + T), id E T + *)  (id * (T + T), id T T + *)
(id * (T + T), id T T + *)  (id * (F + T), id F T + *)
(id * (F + T), id F T + *)  (id * (id + T), id id T + *)
(id * (id + T), id id T + *)  (id * (id + F), id id F + * )
(id * (id + F), id id F + * )  (id * (id + id), id id id + *),
(id * (id + id), id id id + *),
переводящая
эту цепочку
в цепочку
id id id + *.
Рассмотрим
связь
между
переводами,
определяемыми
СУ-схемами и
осуществляемыми
МП-преобразователями [2].
Теорема 5.1. Пусть P -
МП-преобразователь.
Существует
такая
простая
СУ-схема Tr,
что  (Tr) =
(Tr) =  (P).
(P).
Теорема 5.2. Пусть Tr -
простая
СУ-схема.
Существует
такой
МП-преобразователь
P, что  (P) =
(P) =  (Tr).
(Tr).
Таким
образом,
класс
переводов,
определяемых
магазинными
преобразователями,
совпадает
с классом
простых
СУ-переводов.
Рассмотрим
теперь
связь
между
СУ-переводами
и детерминированными
МП-преобразователями,
выполняющими
нисходящий
или
восходящий
разбор [2].
Теорема 5.3. Пусть Tr = (N, T,  , R, S)
- простая
СУ-схема,
входной
грамматикой
которой
служит
LL(1)-грамматика.
Тогда
перевод
{x$, y)|(x, y)
, R, S)
- простая
СУ-схема,
входной
грамматикой
которой
служит
LL(1)-грамматика.
Тогда
перевод
{x$, y)|(x, y) 
 (Tr)} можно
осуществить
детерминированным
МП-преобразователем.
(Tr)} можно
осуществить
детерминированным
МП-преобразователем.
Существуют
простые
СУ-схемы,
имеющие в
качестве
входных
грамматик
LR(1)-грамматики
и не
реализуемые
ни на каком
ДМП-преобразователе.
Пример 5.3. Рассмотрим
простую
СУ-схему с
правилами
Входная
грамматика
является
LR(1)-грамматикой,
но не
существует
ДМП-преобразователя,
определяющего
перевод
{(x$, y)|(x, y) 
 (Tr)}.
(Tr)}.
Назовем
СУ-схему Tr = (N, T,  , R, S)
постфиксной,
если каждое
правило
из R имеет
вид A
, R, S)
постфиксной,
если каждое
правило
из R имеет
вид A  u, v, где
v
u, v, где
v  N*
N* *. Иными
словами,
каждый
элемент
перевода
представляет
собой
цепочку из
нетерминалов,
за которыми
следует
цепочка
выходных
символов.
*. Иными
словами,
каждый
элемент
перевода
представляет
собой
цепочку из
нетерминалов,
за которыми
следует
цепочка
выходных
символов.
Теорема 5.4. Пусть Tr -
простая
постфиксная
СУ-схема,
входная
грамматика
для которой
является
LR(1). Тогда
перевод
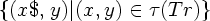
можно
осуществить
детерминированным
МП-преобразователем.
5.2.2 Обобщенные
схемы
синтаксически
управляемого
перевода
Расширим
определение
СУ-схемы, с
тем чтобы
выполнять
более
широкий
класс
переводов.
Во-первых,
позволим
иметь в
каждой
вершине
дерева
разбора
несколько
переводов.
Как и в
обычной
СУ-схеме,
каждый
перевод
зависит
от прямых
потомков
соответствующей
вершины
дерева.
Во-вторых,
позволим
элементам
перевода
быть
произвольными
цепочками
выходных
символов и
символов,
представляющих
переводы в
потомках.
Таким
образом,
символы
перевода
могут
повторяться
или вообще
отсутствовать.
Определение. Обобщенной
схемой
синтаксически
управляемого
перевода (или
трансляции,
сокращенно:
OСУ-схемой)
называется
шестерка
Tr = (N, T,  ,
, 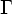 , R, S), где все
символы
имеют тот
же смысл,
что и для
СУ-схемы, за
исключением
того, что
, R, S), где все
символы
имеют тот
же смысл,
что и для
СУ-схемы, за
исключением
того, что
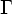 - конечное
множество
символов
перевода
вида Ai, где
A
- конечное
множество
символов
перевода
вида Ai, где
A  N и i - целое
число;
N и i - целое
число;
- R - конечное
множество
правил перевода
вида
A  u, A1 = v1, ..., Am = vm,
u, A1 = v1, ..., Am = vm,
удовлетворяющих
следующим
условиям:
- Aj

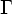 для 1
для 1  j
j  m,
m,
- каждый символ,
входящий
в v1, ..., vm, либо
принадлежит
 , либо является
Bk
, либо является
Bk 
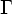 , где B входит
в u,
, где B входит
в u,
- если u имеет
более одного
вхождения
символа
B, то каждый
символ Bk
во всех v
соотнесен
(верхним
индексом)
с конкретным
вхождением
B.
A  u называют
входным
правилом
вывода, Ai -
переводом
нетерминала
A, Ai = vi - элементом
перевода,
связанным
с этим
правилом
перевода.
Если в
ОСУ-схеме
нет двух
правил
перевода с
одинаковым
входным
правилом
вывода, то
ее называют
семантически
однозначной.
u называют
входным
правилом
вывода, Ai -
переводом
нетерминала
A, Ai = vi - элементом
перевода,
связанным
с этим
правилом
перевода.
Если в
ОСУ-схеме
нет двух
правил
перевода с
одинаковым
входным
правилом
вывода, то
ее называют
семантически
однозначной.
Выход
ОСУ-схемы
определим
снизу
вверх. С
каждой
внутренней
вершиной
n дерева
разбора
(во входной
грамматике),
помеченной A,
свяжем одну
цепочку для
каждого Ai.
Эта цепочка
называется
значением
(или
переводом)
символа Ai
в вершине
n. Каждое
значение
вычисляется
подстановкой
значений
символов
перевода
данного
элемента
перевода Ai = vi,
определенных
в прямых
потомках
вершины n.
Переводом  (Tr),
определяемым
ОСУ-схемой
Tr, назовем
множество
{(x, y) | x имеет
дерево
разбора во
входной
грамматике
для Tr и y -
значение
выделенного
символа
перевода
Sk в корне
этого
дерева}.
(Tr),
определяемым
ОСУ-схемой
Tr, назовем
множество
{(x, y) | x имеет
дерево
разбора во
входной
грамматике
для Tr и y -
значение
выделенного
символа
перевода
Sk в корне
этого
дерева}.
Пример 5.4. Рассмотрим
формальное
дифференцирование
выражений,
включающих
константы 0 и
1, переменную
x, функции sin
и cos , а также
операции
* и +. Такие
выражения
порождает
грамматика
| E  E + T | T |
| T  T * F | F |
| F  (E) | sin (E) | cos (E) | x | 0 | 1 |
|
Свяжем
с каждым
из E, T и F два
перевода,
обозначенных
индексом 1
и 2. Индекс 1
указывает
на то, что
выражение не
дифференцировано,
2 - что
выражение
продифференцировано.
Формальная
производная
- это E2. Законы
дифференцирования
таковы:
d(f(x) + g(x)) = df(x) + dg(x) |
d(f(x) * g(x)) = f(x) * dg(x) + g(x) * df(x) |
d sin (f(x)) = cos (f(x)) * df(x) |
d cos (f(x)) = - sin (f(x))df(x) |
dx = 1 |
d0 = 0 |
d1 = 0 |
|
Эти законы
можно
реализовать
следующей
ОСУ-схемой:
E  E + T | E1 = E1 + T1 |
| E2 = E2 + T2 |
|
E  T | E1 = T1 |
| E2 = T2 |
|
T  T * F | T1 = T1 * F1 |
| T2 = T1 * F2 + T2 * F1 |
|
T  F | T1 = F1 |
| T2 = F2 |
|
F  (E) | F1 = (E1) |
| F2 = (E2) |
|
F  sin (E) | F1 = sin (E1) |
| F2 = cos (E1) * (E2) |
|
F  cos (E) | F1 = cos (E1) |
| F2 = - sin (E1) * (E2) |
|
F  x | F1 = x |
| F2 = 1 |
|
F  0 | F1 = 0 |
| F2 = 0 |
|
F  1 | F1 = 1 |
| F2 = 0 |
|
Дерево
вывода для
sin(cos (x))+x приведено
на рис. 5.1.
5.3 Атрибутные
грамматики
Среди всех
формальных
методов
описания
языков
программирования
атрибутные
грамматики
(введенные
Кнутом [6])
получили,
по-видимому,
наибольшую
известность
и распространение.
Причиной
этого
является
то, что
формализм
атрибутных
грамматик
основывается
на дереве
разбора
программы в
КС-грамматике,
что
сближает
его с хорошо
разработанной
теорией и
практикой
построения
трансляторов.
5.3.1 Определение
атрибутных
грамматик
Атрибутной
грамматикой
называется
четверка
AG = (G, AS, AI, R), где
- G = (N, T, P, S) - приведенная
КС-грамматика;
- AS - конечное
множество
синтезируемых
атрибутов;
- AI - конечное
множество
наследуемых
атрибутов,
AS
 AI =
AI = 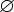 ;
;
- R - конечное
множество
семантических
правил.
Атрибутная
грамматика AG
сопоставляет
каждому
символу X из N  T
множество AS(X)
синтезируемых
атрибутов и
множество AI(X)
наследуемых
атрибутов.
Множество
всех
синтезируемых
атрибутов
всех
символов из N
T
множество AS(X)
синтезируемых
атрибутов и
множество AI(X)
наследуемых
атрибутов.
Множество
всех
синтезируемых
атрибутов
всех
символов из N  T
обозначается
AS, наследуемых
- AI. Атрибуты
разных
символов
являются
различными
атрибутами.
Будем
обозначать
атрибут a
символа X как
a(X). Значения
атрибутов
могут быть
произвольных
типов,
например,
представлять
собой
числа,
строки,
адреса
памяти и
т.д.
T
обозначается
AS, наследуемых
- AI. Атрибуты
разных
символов
являются
различными
атрибутами.
Будем
обозначать
атрибут a
символа X как
a(X). Значения
атрибутов
могут быть
произвольных
типов,
например,
представлять
собой
числа,
строки,
адреса
памяти и
т.д.
Пусть
правило p
из P имеет
вид X0  X1X2...Xn.
Атрибутная
грамматика AG
сопоставляет
каждому
правилу p из
P конечное
множество R(p)
семантических
правил
вида
X1X2...Xn.
Атрибутная
грамматика AG
сопоставляет
каждому
правилу p из
P конечное
множество R(p)
семантических
правил
вида

где 0  j, k, ..., m
j, k, ..., m  n,
причем
1
n,
причем
1  i
i  n, если
a(Xi)
n, если
a(Xi)  AI(Xi) (т.е. a(Xi) -
наследуемый
атрибут),
и i = 0, если
a(Xi)
AI(Xi) (т.е. a(Xi) -
наследуемый
атрибут),
и i = 0, если
a(Xi)  AS(Xi) (т.е. a(Xi) -
синтезируемый
атрибут).
AS(Xi) (т.е. a(Xi) -
синтезируемый
атрибут).
Таким
образом,
семантическое
правило
определяет
значение
атрибута
a символа Xi
на основе
значений
атрибутов b, c, ...,
d символов Xj, Xk, ..., Xm
соответственно.
В частном
случае
длина n
правой
части
правила
может
быть равна
нулю, тогда
будем
говорить,
что атрибут
a символа Xi
«получает
в качестве
значения
константу».
В дальнейшем
будем
считать, что
атрибутная
грамматика
не содержит
семантических
правил для
вычисления
атрибутов
терминальных
символов.
Предполагается,
что
атрибуты
терминальных
символов
- либо
предопределенные
константы,
либо
доступны
как
результат
работы
лексического
анализатора.
Пример 5.5. Рассмотрим
атрибутную
грамматику,
позволяющую
вычислить
значение
вещественного
числа,
представленного
в десятичной
записи.
Здесь N = {Num, Int, Frac}, T = {digit, .},
S = Num, а правила
вывода и
семантические
правила
определяются
следующим
образом
(верхние
индексы
используются
для ссылки
на разные
вхождения
одного и
того же
нетерминала):
Num  Int . Frac | v(Num) = v(Int) + v(Frac) |
| p(Frac) = 1 |
|
Int  e | v(Int) = 0 |
| p(Int) = 0 |
|
Int 1  digit Int 2 | v(Int1) = v(digit) * 10p(Int2) + v(Int2) |
| p(Int1) = p(Int2) + 1 |
|
Frac  e | v(Frac) = 0 |
|
Frac 1  digit Frac 2 | v(Frac1) = v(digit) * 10-p(Frac1) + v(Frac2) |
| p(Frac2) = p(Frac1) + 1 |
|
Для этой
грамматики
| AS(Num) = {v}, | AI(Num) = 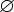 , , |
| AS(Int) = {v, p}, | AI(Int) = 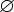 , , |
| AS(Frac) = {v}, | AI(Frac) = {p}. |
| |
Пусть дана
атрибутная
грамматика
AG и цепочка,
принадлежащая
языку,
определяемому
соответствующей
G = (N, T, P, S). Сопоставим
этой
цепочке
«значение»
следующим
образом.
Построим
дерево
разбора
T этой
цепочки в
грамматике
G. Каждый
внутренний
узел этого
дерева
помечается
нетерминалом
X0, соответствующим
применению
p-го правила
грамматики;
таким
образом,
у этого
узла будет n
непосредственных
потомков
(рис. 5.2).
Пусть
теперь X
- метка
некоторого
узла дерева
и пусть a -
атрибут
символа
X. Если a -
синтезируемый
атрибут,
то X = X0 для
некоторого
p  P; если же a -
наследуемый
атрибут,
то X = Xj для
некоторых
p
P; если же a -
наследуемый
атрибут,
то X = Xj для
некоторых
p  P и 1
P и 1  j
j  n. В обоих
случаях
дерево «в
районе»
этого узла
имеет вид,
приведенный
на рис. 5.2. По
определению,
атрибут
a имеет в
этом узле
значение
v, если в
соответствующем
семантическом
правиле
n. В обоих
случаях
дерево «в
районе»
этого узла
имеет вид,
приведенный
на рис. 5.2. По
определению,
атрибут
a имеет в
этом узле
значение
v, если в
соответствующем
семантическом
правиле
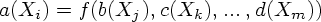
все
атрибуты
b, c, ..., d уже
определены
и имеют в
узлах с
метками X
j, X
k, ..., X
m
значения v
j, v
k, ..., v
m
соответственно,
а v = f(v
1, v
2, ..., v
m). Процесс
вычисления
атрибутов
на дереве
продолжается
до тех
пор, пока
нельзя
будет
вычислить
больше ни
одного
атрибута.
Вычисленные
в результате
атрибуты
корня
дерева
представляют
собой
«значение»,
соответствующее
данному
дереву
вывода.
Заметим, что
значение
синтезируемого
атрибута
символа
в узле
синтаксического
дерева
вычисляется
по атрибутам
символов в
потомках
этого узла;
значение
наследуемого
атрибута
вычисляется
по атрибутам
«родителя'
и «соседей».
Атрибуты,
сопоставленные
вхождениям
символов
в дерево
разбора,
будем
называть
вхождениями
атрибутов
в дерево
разбора, а
дерево с
сопоставленными
каждой
вершине
атрибутами
- атрибутированным
деревом
разбора.
Пример 5.6. Атрибутированное
дерево для
грамматики из
предыдущего
примера и
цепочки w = 12.34
показано
на рис. 5.3.
Будем
говорить,
что
семантические
правила
заданы
корректно,
если они
позволяют
вычислить
все
атрибуты
произвольного
узла в
любом
дереве
вывода.
Между
вхождениями
атрибутов
в дерево
разбора
существуют
зависимости,
определяемые
семантическими
правилами,
соответствующими
примененным
синтаксическим
правилам.
Эти
зависимости
могут быть
представлены
в виде
ориентированного
графа
следующим
образом.
Пусть T -
дерево
разбора.
Сопоставим
этому
дереву
ориентированный
граф D(T),
узлами
которого
являются
пары (n, a), где
n - узел
дерева T, a -
атрибут
символа,
служащего
меткой
узла n. Граф
содержит
дугу из (n1, a1)
в (n2, a2) тогда
и только
тогда,
когда
семантическое
правило,
вычисляющее
атрибут a2,
непосредственно
использует
значение
атрибута
a1. Таким
образом,
узлами
графа D(T)
являются
атрибуты,
которые
нужно
вычислить,
а дуги
определяют
зависимости,
подразумевающие,
какие
атрибуты
вычисляются
раньше,
а какие
позже.
Пример 5.7. Граф
зависимостей
атрибутов
для дерева
разбора из
предыдущего
примера
показан на
рис. 5.4.
Можно
показать,
что
семантические
правила
являются
корректными
тогда и
только
тогда,
когда для
любого
дерева
вывода T
соответствующий
граф D(T) не
содержит
циклов (т.е.
является
ориентированным
ациклическим
графом).
5.3.2 Классы
атрибутных
грамматик
и их
реализация
В общем виде
реализация
вычислителей
для
атрибутных
грамматик
вызывает
значительные
трудности.
Это связано
с тем, что
множество
значений
атрибутов,
связанных
с данным
деревом,
приходится
вычислять в
соответствии
с зависимостями
атрибутов,
которые
образуют
ориентированный
ациклический
граф. На
практике
стараются
осуществлять
процесс
вычисления
атрибутов,
привязывая
его к тому
или иному
способу
обхода
дерева.
Рассматривают
многовизитные,
многопроходные
и другие
атрибутные
вычислители.
Это, как
правило,
ведет к
ограничению
допустимых
зависимостей
между
атрибутами,
поддерживаемых
вычислителем.
Простейшими
подклассами
атрибутных
грамматик,
вычисления
всех
атрибутов
для которых
может быть
осуществлено
одновременно
с синтаксическим
анализом,
являются
S-атрибутные
и L-атрибутные
грамматики.
Определение. Атрибутная
грамматика
называется
S-атрибутной,
если она
содержит
только
синтезируемые
атрибуты.
Нетрудно
видеть,
что для
S-атрибутной
грамматики
на любом
дереве
разбора все
атрибуты
могут быть
вычислены
за один
обход
дерева
снизу
вверх.
Таким
образом,
вычисление
атрибутов
можно
делать
параллельно
с восходящим
синтаксическим
анализом,
например,
LR(1)-анализом.
Пример 5.8. Рассмотрим
S-атрибутную
грамматику
для перевода
арифметических
выражений в
ПОЛИЗ. Здесь
атрибут
v имеет
строковый
тип,
|| - обозначает
операцию
конкатенации.
Правила
вывода и
семантические
правила
определяются
следующим
образом
E 1  E 2 + T | v(E1) = v(E2) || v(T) ||' + ' |
|
E  T | v(E) = v(T) |
|
T  T * F | v(T1) = v(T2) || v(F) ||'*' |
|
T  F | v(T) = v(F) |
|
F  id | v(F) = v(id) |
|
F  (E) | v(F) = v(E) |
|
Определение. Атрибутная
грамматика
называется
L-атрибутной,
если любой
наследуемый
атрибут
любого
символа Xj
из правой
части
каждого
правила X0  X1X2...Xn
грамматики
зависит
только
от
X1X2...Xn
грамматики
зависит
только
от
- атрибутов
символов
X1, X2, ..., Xj-1, находящихся
в правиле
слева от
Xj, и
- наследуемых
атрибутов
символа
X0.
Заметим,
что каждая
S-атрибутная
грамматика
является
L-атрибутной.
Все
атрибуты
на любом
дереве для
L-атрибутной
грамматики
могут быть
вычислены
за один
обход
дерева
сверху-вниз
слева-направо.
Таким
образом,
вычисление
атрибутов
можно
осуществлять
параллельно
с нисходящим
синтаксическим
анализом,
например,
LL(1)-анализом
или
рекурсивным
спуском.
В случае
рекурсивного
спуска в
каждой
функции,
соответствующей
нетерминалу,
надо
определить
формальные
параметры,
передаваемые
по значению,
для
наследуемых
атрибутов, и
формальные
параметры,
передаваемые
по ссылке,
для
синтезируемых
атрибутов.
В качестве
примера
рассмотрим
реализацию
атрибутной
грамматики
из примера
5.5 (нетрудно
видеть, что
грамматика
является
L-атрибутной).
void int_part(float * V0, int * P0)
{if (Map[InSym]==Digit)
{ int I=InSym;
float V2;
int P2;
InSym=getInSym();
int_part(&V2,&P2);
*V0=I*exp(P2*ln(10))+V2;
*P0=P2+1;
}
else {*V0=0;
*P0=0;
}
}
void fract_part(float * V0, int P0)
{if (Map[InSym]==Digit)
{ int I=InSym;
float V2;
int P2=P0+1;
InSym=getInSym();
fract_part(&V2,P2);
*V0=I*exp(-P0*ln(10))+V2;
}
else {*V0=0;
}
}
void number()
{ float V1,V3,V0;
int P;
int_part(&V1,&P);
if (InSym!='.') error();
fract_part(&V3,1);
V0=V1+V3;
}
|
5.3.3 Язык
описания
атрибутных
грамматик
Формализм
атрибутных
грамматик
оказался
очень
удобным
средством
для
описания
семантики
языков
программирования.
Вместе с тем
выяснилось,
что
реализация
вычислителей
для
атрибутных
грамматик
общего вида
сталкивается
с большими
трудностями.
В связи с
этим было
сделано
множество
попыток
рассматривать
те или иные
классы
атрибутных
грамматик,
обладающих
«хорошими»
свойствами.
К числу
таких
свойств
относятся
прежде
всего
простота
алгоритма
проверки
атрибутной
грамматики
на зацикленность
и простота
алгоритма
вычисления
атрибутов
для
атрибутных
грамматик
данного
класса.
Атрибутные
грамматики
использовались
для
описания
семантики
языков
программирования
и было
создано
несколько
систем
автоматизации
разработки
трансляторов,
основанных
на формализме
атрибутных
грамматик.
Опыт их
использования
показал, что
«чистый»
атрибутный
формализм
может быть
успешно
применен
для
описания
семантики
языка,
но его
использование
вызывает
трудности
при
создании
транслятора.
Эти
трудности
связаны
как с самим
формализмом,
так и с
некоторыми
технологическими
проблемами.
К трудностям
первого
рода можно
отнести
несоответствие
чисто
функциональной
природы
атрибутного
вычислителя
и связанной
с ней
неупорядоченностью
процесса
вычисления
атрибутов
(что в
значительной
степени
является
преимуществом
этого
формализма)
и упорядоченностью
элементов
программы.
Это
несоответствие
ведет к
тому, что
приходится
идти на
искусственные
приемы
для их
сочетания.
Технологические
трудности
связаны с
эффективностью
трансляторов,
полученных
с помощью
атрибутных
систем. Как
правило,
качество
таких
трансляторов
довольно
низко из-за
больших
расходов
памяти,
неэффективности
искусственных
приемов,
о которых
было
сказано
выше.
Учитывая
это, мы
будем
вести
дальнейшее
изложение
на языке,
сочетающем
особенности
атрибутного
формализма
и обычного
языка
программирования,
в котором
предполагается
наличие
операторов,
а значит, и
возможность
управления
порядком
исполнения
операторов.
Этот
порядок
может быть
привязан
к обходу
атрибутированного
дерева
разбора
сверху
вниз слева
направо. Что
касается
грамматики
входного
языка, то
мы не будем
предполагать
принадлежность
ее определенному
классу
(например, LL(1)
или LR(1)). Будем
считать,
что дерево
разбора
входной
программы
уже
построено
как
результат
синтаксического
анализа и
атрибутные
вычисления
осуществляются
в результате
обхода
этого
дерева.
Таким
образом,
входная
грамматика
атрибутного
вычислителя
может
быть даже
неоднозначной,
что не
влияет на
процесс
атрибутных
вычислений.
При записи
синтаксиса
мы будем
использовать
расширенную
БНФ. Элемент
правой
части
синтаксического
правила,
заключенный
в скобки
[ ], может
отсутствовать.
Элемент
правой
части
синтаксического
правила,
заключенный
в скобки ( ),
означает
возможность
повторения
один или
более раз.
Элемент
правой
части
синтаксического
правила,
заключенный
в скобки [()],
означает
возможность
повторения
ноль или
более раз.
В скобках [ ]
или [()] может
указываться
разделитель
конструкций.
Ниже дан
синтаксис
языка
описания
атрибутных
грамматик.
Приведен
только
синтаксис
конструкций,
собственно
описывающих
атрибутные
вычисления.
Синтаксис
обычных
выражений и
операторов
не приводится
- он
основывается
на Си.
Атрибутная грамматика ::= 'ALPHABET'
( ОписаниеНетерминала ) ( Правило )
ОписаниеНетерминала ::= ИмяНетерминала
'::' [( ОписаниеАтрибутов / ';')] '.'
ОписаниеАтрибутов ::= Тип ( ИмяАтрибута / ',')
Правило ::= 'RULE' Синтаксис 'SEMANTICS' Семантика '.'
Синтаксис ::= ИмяНетерминала '::=' ПраваяЧасть
ПраваяЧасть ::= [( ЭлементПравойЧасти )]
ЭлементПравойЧасти ::= ИмяНетерминала
| Терминал
| '(' Нетерминал [ '/' Терминал ] ')'
| '[' Нетерминал ']'
| '[(' Нетерминал [ '/' Терминал ] ')]'
Семантика ::= [(ЛокальноеОбъявление / ';')]
[( СемантическоеДействие / ';')]
СемантическоеДействие ::= Присваивание
| [ Метка ] Оператор
Присваивание ::= Переменная ':=' Выражение
Переменная ::= ЛокальнаяПеременная
| Атрибут
Атрибут ::= ЛокальныйАтрибут
| ГлобальныйАтрибут
ЛокальныйАтрибут ::= ИмяАтрибута '<' Номер '>'
ГлобальныйАтрибут ::= ИмяАтрибута '<' Нетерминал '>'
Метка ::= Целое ':'
| Целое 'Е' ':'
| Целое 'А' ':'
Оператор ::= Условный
| ОператорПроцедуры
| ЦиклПоМножеству
| ПростойЦикл
| ЦиклСУсловиемОкончания
|
Описание
атрибутной
грамматики
состоит из
раздела
описания
атрибутов
и раздела
правил.
Раздел
описания
атрибутов
определяет
состав
атрибутов
для каждого
символа
грамматики
и тип
каждого
атрибута.
Правила
состоят из
синтаксической
и семантической
части. В
синтаксической
части
используется
расширенная
БНФ.
Семантическая
часть
правила
состоит из
локальных
объявлений
и семантических
действий.
В качестве
семантических
действий
допускаются
как
атрибутные
присваивания,
так и
составные
операторы.
Метка в
семантической
части
правила
привязывает
выполнение
оператора
к обходу
дерева
разбора
сверху-вниз
слева
направо.
Конструкция
i : оператор
означает,
что
оператор
должен быть
выполнен
сразу
после
обхода i-й
компоненты
правой
части.
Конструкция
i E : оператор
означает,
что
оператор
должен быть
выполнен,
только если
порождение
i-й компоненты
правой
части
пусто.
Конструкция
i A : оператор
означает,
что
оператор
должен быть
выполнен
после
разбора
каждого
повторения
i-й компоненты
правой
части
(имеется
в виду
конструкция
повторения).
Каждое
правило
может
иметь
локальные
определения
(типов и
переменных).
В формулах
используются
как
атрибуты
символов
данного
правила
(локальные
атрибуты)
и в этом
случае
соответствующие
символы
указываются
номерами в
правиле (0 -
для символа
левой
части, 1 - для
первого
символа
правой
части, 2 - для
второго
символа
правой
части и
т.д.), так и
атрибуты
символов
предков
левой
части
правила
(глобальные
атрибуты).
В этом
случае
соответствующий
символ
указывается
именем
нетерминала.
Таким
образом,
на дереве
образуются
области
видимости
атрибутов:
атрибут
символа
имеет
область
видимости,
состоящую
из правила,
в которое
символ
входит в
правую
часть,
плюс все
поддерево,
корнем
которого
является
символ, за
исключением
поддеревьев
- потомков
того же
символа
в этом
поддереве.
Значение
терминального
символа
доступно
через
атрибут VAL
соответствующего
типа.
Пример 5.9. Атрибутная
грамматика
из примера 5.5
записывается
следующим
образом:
ALPHABET
Num :: float V.
Int :: float V;
int P.
Frac :: float V;
int P.
digit :: int VAL.
RULE
Num ::= Int '.' Frac
SEMANTICS
V<0>=V<1>+V<3>; P<3>=1.
RULE
Int ::= e
SEMANTICS
V<0>=0; P<0>=0.
RULE
Int ::= digit Int
SEMANTICS
V<0>=VAL<1>*10**P<2>+V<2>; P<0>=P<2>+1.
RULE
Frac ::= e
SEMANTICS
V<0>=0.
RULE
Frac ::= digit Frac
SEMANTICS
V<0>=VAL<1>*10**(-P<0>)+V<2>; P<2>=P<0>+1.
|
Назад Оглавление Вперёд