2004 г
Назад Оглавление Вперёд
2. Языки и их
представление
2.1 Алфавиты,
цепочки и
языки
Алфавит, или
словарь - это
конечное
множество
символов. Для
обозначения
символов
мы будем
пользоваться
цифрами,
латинскими
буквами и
специальными
литерами
типа #, $.
Пусть V -
алфавит.
Цепочка в
алфавите V -
это любая
строка
конечной
длины,
составленная
из символов
алфавита V .
Синонимом
цепочки
являются
предложение,
строка
и слово.
Пустая
цепочка
(обозначается
e) - это цепочка,
в которую
не входит
ни один
символ.
Конкатенацией
цепочек x и y
называется
цепочка xy.
Заметим, что
xe = ex = x для любой
цепочки x.
Пусть x, y, z -
произвольные
цепочки в
некотором
алфавите.
Цепочка y
называется
подцепочкой
цепочки xyz.
Цепочки x и y
называются,
соответственно,
префиксом и
суффиксом
цепочки xy.
Заметим,
что любой
префикс или
суффикс
цепочки
является
подцепочкой
этой цепочки.
Кроме того,
пустая
цепочка
является
префиксом,
суффиксом и
подцепочкой
для любой
цепочки.
Пример 2.1. Для цепочки
abbba префиксом
является
любая цепочка
из множества
L1 = {e, a, ab, abb, abbb, abbba}, суффиксом
является
любая
цепочка из
множества L2 = {e, a, ba, bba, bbba, abbba},
подцепочкой
является
любая цепочка
из множества
L1  L2.
L2.
Длиной
цепочки w
(обозначается
|w|) называется
число
символов в
ней. Например,
|abababa| = 7, а |e| = 0.
Язык в
алфавите
V - это
некоторое
множество
цепочек в
алфавите
V .
Пример 2.2. Пусть дан
алфавит V = {a, b}. Вот
некоторые
языки в
алфавите V :
Два последних
языка
содержат
бесконечное
число цепочек.
Введем
обозначение V *
для множества
всех цепочек
в алфавите
V , включая
пустую
цепочку.
Каждый язык
в алфавите
V является
подмножеством
V *. Для
обозначения
множества
всех цепочек
в алфавите
V , кроме
пустой
цепочки,
будем
использовать
V +.
Пример 2.3. Пусть V = {0, 1}.
Тогда V * = {e, 0, 1, 00, 01, 10, 11, 000, ...},
V + = {0, 1, 00, 01, 10, 11, 000, ...}.
Введем
некоторые
операции
над языками.
Пусть L1 и L2
- языки в
алфавите V .
Конкатенацией
языков L1 и L2
называется
язык L1L2 = {xy|x  L1, y
L1, y  L2}.
L2}.
Пусть L
- язык в
алфавите V .
Итерацией
языка L
называется
язык L*,
определяемый
следующим
образом:
- L0 = {e};
- Ln = LLn-1, n
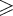 1;
1;
- L* =
 n=0
n=0 Ln.
Ln.
Пример 2.4. Пусть L1 = {aa, bb} и
L2 = {e, a, bb}. Тогда
L1L2 = {aa, bb, aaa, bba, aabb, bbbb}, и
L1* = {e, aa, bb, aaaa, aabb, bbaa, bbbb, aaaaaa, ...}.
Большинство
языков,
представляющих
интерес,
содержат
бесконечное
число
цепочек.
При этом
возникают
три важных
вопроса.
Во-первых, как
представить
язык (т.е.
специфицировать
входящие
в него
цепочки)?
Если язык
содержит
только
конечное
множество
цепочек,
ответ прост.
Можно просто
перечислить
его цепочки.
Если язык
бесконечен,
необходимо
найти
для него
конечное
представление.
Это конечное
представление,
в свою
очередь,
будет
строкой
символов над
некоторым
алфавитом
вместе с
некоторой
интерпретацией,
связывающей
это
представление
с языком.
Во-вторых,
для любого
ли языка
существует
конечное
представление?
Можно
предположить,
что ответ
отрицателен.
Мы увидим, что
множество
всех
цепочек над
алфавитом
счетно. Язык
- это любое
подмножество
цепочек.
Из теории
множеств
известно, что
множество
всех
подмножеств
счетного
множества
несчетно.
Хотя мы и
не дали
строгого
определения
того, что
является
конечным
представлением,
интуитивно
ясно, что
любое
разумное
определение
конечного
представления
ведет только
к счетному
множеству
конечных
представлений,
поскольку
нужно иметь
возможность
записать
такое
конечное
представление
в виде
строки
символов
конечной
длины.
Поэтому
языков
значительно
больше, чем
конечных
представлений.
В-третьих,
можно
спросить,
какова
структура
тех классов
языков, для
которых
существует
конечное
представление?
2.2 Представление
языков
Процедура -
это конечная
последовательность
инструкций,
которые
могут быть
механически
выполнены.
Примером
может
служить
машинная
программа.
Процедура,
которая
всегда
заканчивается,
называется
алгоритмом.
Один из
способов
представления
языка - дать
алгоритм,
определяющий,
принадлежит
ли цепочка
языку. Более
общий способ
состоит в том,
чтобы дать
процедуру,
которая
останавливается
с ответом
«да» для
цепочек,
принадлежащих
языку, и либо
останавливается
с ответом
«нет», либо
вообще не
останавливается
для
цепочек, не
принадлежащих
языку.
Говорят,
что такая
процедура
или алгоритм
распознает
язык.
Такой метод
представляет
язык с точки
зрения
распознавания.
Язык можно
также
представить
методом
порождения.
А именно,
можно дать
процедуру,
которая
систематически
порождает в
определенном
порядке
цепочки
языка.
Если мы
можем
распознать
цепочки
языка над
алфавитом
V либо с
помощью
процедуры,
либо с
помощью
алгоритма,
то мы можем и
генерировать
язык,
поскольку
мы можем
систематически
генерировать
все цепочки
из V *, проверять
каждую
цепочку на
принадлежность
языку и
выдавать
список
только
цепочек
языка.
Но если
процедура
не всегда
заканчивается
при проверке
цепочки, мы
не сдвинемся
дальше
первой
цепочки,
на которой
процедура не
заканчивается.
Эту проблему
можно обойти,
организовав
проверку
таким
образом,
чтобы
процедура
никогда не
продолжала
проверять
одну цепочку
бесконечно.
Для этого
введем
следующую
конструкцию.
Предположим,
что V имеет p
символов.
Мы можем
рассматривать
цепочки из
V * как числа,
представленные
в базисе p,
плюс пустая
цепочка
e. Можно
занумеровать
цепочки в
порядке
возрастания
длины и в
«числовом»
порядке для
цепочек
одинаковой
длины. Такая
нумерация
для цепочек
языка {a, b, c}*
приведена
на рис. 2.1, а.
Пусть P -
процедура
для проверки
принадлежности
цепочки
языку L.
Предположим,
что P может
быть
представлена
дискретными
шагами,
так что
имеет смысл
говорить
об i-ом шаге
процедуры
для любой
данной
цепочки.
Прежде
чем дать
процедуру
перечисления
цепочек
языка L, дадим
процедуру
нумерации пар
положительных
чисел.
Все
упорядоченные
пары
положительных
чисел (x, y) можно
отобразить
на множество
положительных
чисел
следующей
формулой:

Пары целых
положительных
чисел можно
упорядочить в
соответствии
со значением
z (рис. 2.1, б).
Теперь
можно дать
процедуру
перечисления
цепочек L.
Нумеруем
упорядоченные
пары целых
положительных
чисел -
(1,1), (2,1), (1,2), (3,1), (2,2), ... . При
нумерации
пары (i, j)
генерируем
i-ю цепочку из
V * и применяем
к цепочке
первые
j шагов
процедуры P.
Как только мы
определили,
что
сгенерированная
цепочка
принадлежит
L, добавляем
цепочку
к списку
элементов L.
Если цепочка i
принадлежит
L, это будет
определено P
за j шагов для
некоторого
конечного
j. При
перечислении
(i, j) будет
сгенерирована
цепочку с
номером
i. Легко
видеть,
что эта
процедура
перечисляет
все цепочки
L.
Если мы
имеем
процедуру
генерации
цепочек
языка, то мы
всегда можем
построить
процедуру
распознавания
предложений
языка, но
не всегда
алгоритм. Для
определения
того,
принадлежит
ли x языку
L, просто
нумеруем
предложения
L и сравниваем
x с каждым
предложением.
Если
сгенерировано
x, процедура
останавливается,
распознав,
что x
принадлежит
L. Конечно,
если x не
принадлежит
L, процедура
никогда не
закончится.
Язык,
предложения
которого
могут быть
сгенерированы
процедурой,
называется
рекурсивно
перечислимым.
Язык
рекурсивно
перечислим,
если имеется
процедура,
распознающая
предложения
языка.
Говорят,
что язык
рекурсивен,
если
существует
алгоритм для
распознавания
языка. Класс
рекурсивных
языков
является
собственным
подмножеством
класса
рекурсивно
перечислимых
языков.
Мало того,
существуют
языки, не
являющиеся
даже
рекурсивно
перечислимыми.
2.3 Грамматики
2.3.1 Формальное
определение
грамматики
Для нас
наибольший
интерес
представляет
одна из
систем
генерации
языков -
грамматики.
Понятие
грамматики
изначально
было
формализовано
лингвистами
при изучении
естественных
языков.
Предполагалось,
что это
может помочь
при их
автоматической
трансляции.
Однако,
наилучшие
результаты
в этом
направлении
достигнуты
при
описании не
естественных
языков,
а языков
программирования.
Примером
может
служить
способ
описания
синтаксиса
языков
программирования
при помощи
БНФ - формы
Бэкуса-Наура.
Определение. Грамматика
- это
четверка
G = (N, T, P, S), где
- N - алфавит
нетерминальных
символов;
- T - алфавит
терминальных
символов,
N
 T =
T = 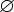 ;
;
- P - конечное
множество
правил вида


 , где
, где 
 (N
(N  T)*N(N
T)*N(N  T)*,
T)*, 
 (N
(N  T)*;
T)*;
- S
 N - начальный
символ (или
аксиома) грамматики.
N - начальный
символ (или
аксиома) грамматики.
Мы будем
использовать
большие
латинские
буквы для
обозначения
нетерминальных
символов,
малые
латинские
буквы из
начала
алфавита для
обозначения
терминальных
символов,
малые
латинские
буквы
из конца
алфавита для
обозначения
цепочек из
T* и, наконец,
малые
греческие
буквы для
обозначения
цепочек из
(N  T)*.
T)*.
Будем
использовать
также
сокращенную
запись A 
 1|
1| 2|...|
2|...| n для
обозначения
группы
правил A
n для
обозначения
группы
правил A 
 1, A
1, A 
 2, ..., A
2, ..., A 
 n.
n.
Определим
на множестве
(N  T)* бинарное
отношение
выводимости
T)* бинарное
отношение
выводимости
 следующим
образом:
если
следующим
образом:
если 

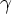
 P, то
P, то 




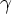
 для всех
для всех  ,
, 
 (N
(N  T)*.
Если
T)*.
Если  1
1 
 2, то
говорят, что
цепочка
2, то
говорят, что
цепочка  2
непосредственно
выводима
из
2
непосредственно
выводима
из  1.
1.
Мы будем
использовать
также
рефлексивно-транзитивное
и транзитивное
замыкания
отношения  ,
а также его
степень k
,
а также его
степень k 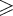 0
(обозначаемые
соответственно
0
(обозначаемые
соответственно
 *,
*,  + и
+ и  k). Если
k). Если  1
1  *
* 2 (
2 ( 1
1  +
+ 2,
2,  1
1  k
k 2),
то говорят,
что цепочка
2),
то говорят,
что цепочка
 2 выводима
(нетривиально
выводима,
выводима
за k шагов)
из
2 выводима
(нетривиально
выводима,
выводима
за k шагов)
из  1.
1.
Если 
 k
k (k
(k 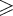 0), то
существует
последовательность
шагов
0), то
существует
последовательность
шагов

где

=
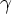 0
0 и

=
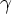 k
k.
Последовательность
цепочек
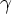 0
0,
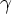 1
1,
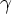 2
2, ...,
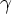 k
k в этом
случае
называют
выводом

из

.
Сентенциальной
формой
грамматики
G называется
цепочка,
выводимая
из ее
начального
символа.
Языком,
порождаемым
грамматикой G
(обозначается
L(G)), называется
множество
всех ее
терминальных
сентенциальных
форм, т.е.

Грамматики G1
и G2 называются
эквивалентными,
если они
порождают
один и тот
же язык, т.е.
L(G1) = L(G2).
Пример 2.5. Грамматика
G = ({S, B, C}, {a, b, c}, P, S), где
P = {S  aSBC, S
aSBC, S  aBC, CB
aBC, CB  BC, aB
BC, aB  ab, bB
ab, bB  bb, bC
bb, bC  bc, cC
bc, cC  cc},
порождает
язык L(G) = {anbncn|n > 0}.
cc},
порождает
язык L(G) = {anbncn|n > 0}.
Действительно,
применяем n- 1
раз правило
1 и получаем
an-1S(BC)n-1, затем
один раз
правило 2 и
получаем an(BC)n,
затем n(n- 1)/2 раз
правило 3 и
получаем
anBnCn.
Затем
используем
правило 4 и
получаем
anbBn-1Cn. Затем
применяем n- 1
раз правило
5 и получаем
anbnCn. Затем
применяем
правило 6 и n - 1
раз правило
7 и получаем
anbncn. Можно
показать,
что язык
L(G) состоит
из цепочек
только
такого вида.
Пример 2.6. Рассмотрим
грамматику
G = ({S}, {0, 1}, {S  0S1, S
0S1, S  01}, S). Легко
видеть, что
цепочка
000111
01}, S). Легко
видеть, что
цепочка
000111  L(G), так как
существует
вывод
L(G), так как
существует
вывод

Нетрудно
показать, что
грамматика
порождает
язык L(G) = {0
n1
n|n > 0}.
Пример 2.7. Рассмотрим
грамматику
G = ({S, A}, {0, 1}, {S  0S,
S
0S,
S  0A, A
0A, A  1A, A
1A, A  1}, S). Нетрудно
показать, что
грамматика
порождает
язык L(G) = {0n1m|n, m > 0}.
1}, S). Нетрудно
показать, что
грамматика
порождает
язык L(G) = {0n1m|n, m > 0}.
2.3.2 Типы
грамматик и
их свойства
Рассмотрим
классификацию
грамматик
(предложенную
Н.Хомским),
основанную
на виде их
правил.
Определение. Пусть дана
грамматика
G = (N, T, P, S). Тогда
Легко
видеть, что
грамматика
в примере 2.5 -
неукорачивающая,
в примере 2.6 -
контекстно-свободная,
в примере 2.7 -
праволинейная.
Язык,
порождаемый
грамматикой
типа i,
называют
языком типа i.
Язык типа 0
называют
также
языком без
ограничений,
язык типа 1 -
контекстно-зависимым
(КЗ), язык
типа 2 -
контекстно-свободным
(КС), язык
типа 3 -
праволинейным.
Теорема 2.1. Каждый
контекстно-свободный
язык
может быть
порожден
неукорачивающей
контекстно-свободной
грамматикой.
Доказательство. Пусть L -
контекстно-свободный
язык. Тогда
существует
контекстно-свободная
грамматика G = (N, T, P, S),
порождающая
L.
Построим
новую
грамматику
G' = (N', T, P', S') следующим
образом:
1. Если в P есть
правило
вида A 
 0B1
0B1 1...Bk
1...Bk k, где
k
k, где
k 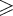 0, Bi
0, Bi  +e для 1
+e для 1  i
i  k, и ни
из одной
цепочки
k, и ни
из одной
цепочки  j (0
j (0  j
j  k) не
выводится e,
то включить в
P' все правила
(кроме A
k) не
выводится e,
то включить в
P' все правила
(кроме A  e) вида
e) вида

где X
i - это
либо B
i, либо
e.
2. Если S  +e, то
включить в P'
правила S'
+e, то
включить в P'
правила S' S, S'
S, S' e и
положить N' = N
e и
положить N' = N  {S'}.
В противном
случае
положить
N' = N и S' = S.
{S'}.
В противном
случае
положить
N' = N и S' = S.
Порождает ли
грамматика
пустую
цепочку
можноо
установить
следующим
простым
алгоритмом:
Шаг 1. Строим
множество
N_0 = N | N  e
e
Шаг 2. Строим
множество
N_i = N | N 

 Ni - 1*
Ni - 1*
Шаг 3. Если N_i =
N_i-1, перейти к
шагу 4, иначе
шаг 2.
Шаг 4. Если S
 Ni, значитS
Ni, значитS  e.
e.
Легко
видеть, что G' -
неукорачивающая
грамматика.
Можно
показать по
индукции,
что L(G') = L(G).
__
Пусть Ki -
класс всех
языков типа i.
Доказано, что
справедливо
следующее
(строгое)
включение:
K3  K2
K2  K1
K1  K0.
K0.
Заметим, что
если язык
порождается
некоторой
грамматикой,
это не
означает,
что он не
может быть
порожден
грамматикой
с более
сильными
ограничениями
на правила.
Приводимый
ниже пример
иллюстрирует
этот факт.
Пример 2.8. Рассмотрим
грамматику
G = ({S, A, B}, {0, 1}, {S  AB,
A
AB,
A  0A, A
0A, A  0, B
0, B  1B, B
1B, B  1}, S). Эта
грамматика
является
контекстно-свободной.
Легко
показать, что
L(G) = {0n1m|n, m > 0}. Однако,
в примере 2.7
приведена
праволинейная
грамматика,
порождающая
тот же язык.
1}, S). Эта
грамматика
является
контекстно-свободной.
Легко
показать, что
L(G) = {0n1m|n, m > 0}. Однако,
в примере 2.7
приведена
праволинейная
грамматика,
порождающая
тот же язык.
Покажем что
существует
алгоритм,
позволяющий
для
произвольного
КЗ-языка L в
алфавите T, и
произвольной
цепочки w  T*
определить,
принадлежит
ли w языку L.
T*
определить,
принадлежит
ли w языку L.
Теорема 2.2. Каждый
контекстно-зависимый
язык
является
рекурсивным
языком.
Доказательство. Пусть L -
контекстно-зависимый
язык. Тогда
существует
некоторая
неукорачивающая
грамматика G = (N, T, P, S),
порождающая
L.
Пусть w  T* и |w| = n.
Если n = 0, т.е. w = e, то
принадлежность
w
T* и |w| = n.
Если n = 0, т.е. w = e, то
принадлежность
w  L проверяется
тривиальным
образом. Так
что будем
предполагать,
что n > 0.
L проверяется
тривиальным
образом. Так
что будем
предполагать,
что n > 0.
Определим
множество Tm
как множество
строк u  (N
(N  T)+
длины не
более n таких,
что вывод
S
T)+
длины не
более n таких,
что вывод
S  *u имеет
не более m
шагов. Ясно,
что T0 = {S}.
*u имеет
не более m
шагов. Ясно,
что T0 = {S}.
Легко
показать,
что Tm можно
получить из Tm-1
просматривая,
какие строки
с длиной,
меньшей
или равной
n можно
вывести из
строк из Tm-1
применением
одного
правила,
т.е.

Если S  *u и
|u|
*u и
|u| n, то u
n, то u  Tm для
некоторого
m. Если из S не
выводится
u или |u| > n, то u не
принадлежит
Tm ни для
какого m.
Tm для
некоторого
m. Если из S не
выводится
u или |u| > n, то u не
принадлежит
Tm ни для
какого m.
Очевидно,
что Tm  Tm-1 для
всех m
Tm-1 для
всех m 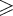 1.
Поскольку
Tm зависит
только от Tm-1,
если Tm = Tm-1, то Tm = Tm+1 = Tm+2 = ...
. Процедура
будет
вычислять
T1, T2, T3, . . . пока для
некоторого m
не окажется
Tm = Tm-1. Если w не
принадлежит
Tm, то не
принадлежит
и L(G), поскольку
для j > m
выполнено
Tj = Tm. Если w
1.
Поскольку
Tm зависит
только от Tm-1,
если Tm = Tm-1, то Tm = Tm+1 = Tm+2 = ...
. Процедура
будет
вычислять
T1, T2, T3, . . . пока для
некоторого m
не окажется
Tm = Tm-1. Если w не
принадлежит
Tm, то не
принадлежит
и L(G), поскольку
для j > m
выполнено
Tj = Tm. Если w  Tm, то
S
Tm, то
S  *w.
*w.
Покажем, что
существует
такое m, что Tm = Tm-1.
Поскольку
для каждого i 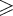 1
справедливо
Ti
1
справедливо
Ti  Ti-1, то если Ti
Ti-1, то если Ti Ti-1,
то число
элементов в
Ti по крайней
мере на 1
больше, чем
в Ti-1. Пусть
|N
Ti-1,
то число
элементов в
Ti по крайней
мере на 1
больше, чем
в Ti-1. Пусть
|N  T| = k. Тогда
число строк
в (N
T| = k. Тогда
число строк
в (N  T)+ длины
меньшей
или равной
n равно k + k2 + ... + kn
T)+ длины
меньшей
или равной
n равно k + k2 + ... + kn  nkn.
Только
эти строки
могут быть
в любом Ti.
Значит, Tm = Tm-1 для
некоторого
m
nkn.
Только
эти строки
могут быть
в любом Ti.
Значит, Tm = Tm-1 для
некоторого
m  nkn. Таким
образом,
процедура,
вычисляющая
Ti для всех
i
nkn. Таким
образом,
процедура,
вычисляющая
Ti для всех
i 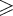 1 до тех
пор, пока
не будут
найдены
два равных
множества,
гарантированно
заканчивается,
значит, это
алгоритм. __
1 до тех
пор, пока
не будут
найдены
два равных
множества,
гарантированно
заканчивается,
значит, это
алгоритм. __
Назад Оглавление Вперёд