Общие сведения о блочных шифрах
Характерной особенностью блочных криптоалгоритмов является тот
факт, что в ходе своей работы они производят преобразование блока входной
информации фиксированной длины и получают результирующий блок того
же объема, но недоступный для прочтения сторонним лицам, не владеющим
ключом. Таким образом, схему работы блочного шифра можно описать функциями
Z=EnCrypt(X,Key)
и X=DeCrypt(Z,Key)
Ключ Key является параметром блочного
криптоалгоритма и представляет
собой некоторый блок двоичной информации фиксированного размера. Исходный
(X) и зашифрованный
(Z) блоки данных также имеют фиксированную разрядность,
равную между собой, но необязательно равную длине ключа.
Блочные шифры являются основой, на которой реализованы практически
все криптосистемы. Методика создания цепочек из зашифрованных блочными
алгоритмами байт позволяет шифровать ими пакеты информации неограниченной
длины. Такое свойство блочных шифров, как быстрота работы, используется
асимметричными криптоалгоритмами, медлительными по своей природе. Отсутствие
статистической корреляции между битами выходного потока блочного шифра
используется для вычисления контрольных сумм пакетов данных и в хешировании
паролей.
Следующие разработки всемирно признаны стойкими алгоритмами и публикаций
о универсальных методах их взлома в средствах массовой информации на
момент создания материала не встречалось.
| Название алгоритма | Автор | Размер блока | Длина ключа |
|---|
| IDEA |
Xuejia Lia and James Massey |
64 бита | 128 бит |
| CAST128 |
|
64 бита | 128 бит |
| BlowFish |
Bruce Schneier |
64 бита | 128 – 448 бит |
| ГОСТ |
НИИ *** |
64 бита | 256 бит |
| TwoFish |
Bruce Schneier |
128 бит | 128 – 256 бит |
| MARS |
Корпорация IBM |
128 бит | 128 – 1048 бит |
Криптоалгоритм именуется идеально стойким,
если прочесть
зашифрованный блок данных можно только перебрав все возможные ключи,
до тех пор, пока сообщение не окажется осмысленным. Так как по теории
вероятности искомый ключ будет найден с вероятностью 1/2 после перебора
половины всех ключей, то на взлом идеально стойкого криптоалгоритма
с ключом длины N потребуется в среднем
2N-1 проверок. Таким
образом, в общем случае стойкость блочного шифра зависит только от
длины ключа и возрастает экспоненциально с ее ростом. Даже предположив,
что перебор ключей производится на специально созданной многопроцессорной
системе, в которой благодаря диагональному параллелизму на проверку
1 ключа уходит только 1 такт, то на взлом 128 битного ключа современной
технике потребуется не менее
1021 лет. Естественно,
все сказанное относится только к идеально стойким шифрам, которыми,
например, с большой долей уверенности являются приведенные в таблице
выше алгоритмы.
Кроме этого условия к идеально стойким криптоалгоритмам применяется
еще одно очень важное требование, которому они должны обязательно соответствовать.
При известных исходном и зашифрованном значениях блока ключ, которым
произведено это преобразование, можно узнать также только полным перебором.
Ситуации, в которых постороннему наблюдателю известна часть исходного
текста встречаются повсеместно. Это могут быть стандартные надписи
в электронных бланках, фиксированные заголовки форматов файлов, довольно
часто встречающиеся в тексте длинные слова или последовательности байт.
В свете этой проблемы описанное выше требование не является ничем чрезмерным
и также строго выполняется стойкими криптоалгоритмами, как и первое.
Таким образом, на функцию стойкого блочного шифра
Z=EnCrypt(X,Key)
накладываются следующие условия:
- Функция EnCrypt должна быть обратимой.
- Не должно существовать иных методов прочтения сообщения
X по
известному блоку Z, кроме как полным перебором
ключей Key.
- Не должно существовать иных методов определения каким ключом
Key было произведено преобразование известного
сообщения X в сообщение
Z, кроме как полным перебором ключей.
Давайте рассмотрим методы, с помощью которых разработчики блочных
криптоалгоритмов добиваются одновременного выполнения этих трех условий
с очень большой долей достоверности.
Все действия, производимые над данными блочным криптоалгоритмом,
основаны на том факте, что преобразуемый блок может быть представлен
в виде целого неотрицательного числа из диапазона, соответствующего
его разрядности. Так, например, 32-битный блок данных можно интерпретировать
как число из диапазона 0..4'294'967'295. Кроме того, блок, разрядность
которого обычно является "степенью двойки", можно трактовать как несколько
независимых неотрицательных чисел из меньшего диапазона (рассмотренный
выше 32-битный блок можно также представить в виде 2 независимых чисел
из диапазона 0..65535 или в виде 4 независимых чисел из диапазона 0..255).
Над этими числами блочным криптоалгоритмом и производятся по определенной
схеме следующие действия (слева даны условные обозначения этих операций
на графических схемах алгоритмов) :
|
Биективные математические функции |
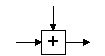 |
Сложение |
X'=X+V |
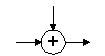 |
Исключающее ИЛИ |
X'=X XOR V |
| |
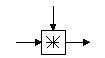
Умножение по модулю 2N+1 |
X'=(X*V) mod (2N+1) |
 |
Умножение по модулю 2N |
X'=(X*V) mod (2N) |
|
Битовые сдвиги |
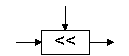 |
Арифметический сдвиг влево |
X'=X SHL V |
 |
Арифметический сдвиг вправо |
X'=X SHR V |
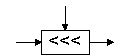 |
Циклический сдвиг влево |
X'=X ROL V |
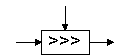 |
Циклический сдвиг вправо |
X'=X ROR V |
|
Табличные подстановки |
 |
S-box (англ. substitute) |
X'=Table[X,V] |
В качестве параметра V для любого из этих преобразований может
использоваться:
- фиксированное число
(например, X'=X+125)
- число, получаемое из ключа
(например, X'=X+F(Key))
- число, получаемое из независимой части блока
(например, X2'=X2+F(X1))
Последний вариант используется в схеме, названной по имени ее создателя
сетью Фейштеля
(нем. Feistel).
Последовательность выполняемых над блоком операций, комбинации
перечисленных выше вариантов V и сами
функции F и составляют "ноу-хау"
каждого конкретного блочного криптоалгоритма. Размер блоков и длина
ключа современных (1999 год) алгоритмов были нами
рассмотрены ранее. Один-два раза в год исследовательские центры
мира публикуют очередной блочный шифр, который под яростной атакой
криптоаналитиков либо приобретает за несколько лет статус стойкого
криптоалгоритма, либо (что происходит неизмеримо чаще) бесславно уходит
в историю криптографии.
Характерным признаком блочных алгоритмов является многократное
и косвенное использование материала ключа. Это диктуется в первую очередь
требованием невозможности обратного декодирования в отношении ключа
при известных исходном и зашифрованном текстах. Для решения этой задачи
в приведенных выше преобразованиях чаще всего используется не само
значение ключа или его части, а некоторая, иногда необратимая (небиективная)
функция от материала ключа. Более того, в подобных преобразованиях
один и тот же блок или элемент ключа используется многократно. Это
позволяет при выполнении условия обратимости функции относительно величины
X сделать функцию необратимой относительно
ключа Key.
Поскольку операция зашифровки или расшифровки отдельного блока
в процессе кодирования пакета информации выполняется многократно (иногда
до сотен тысяч раз), а значение ключа и, следовательно,
функций Vi(Key)
остается неизменным, то иногда становится целесообразно заранее однократно
вычислить данные значения и хранить их в оперативной памяти совместно
с ключом. Поскольку эти значения зависят только от ключа, то оин
в криптографии называются материалом ключа.
Необходимо отметить, что данная операция никоим
образом не изменяет ни длину ключа, ни криптостойкость алгоритма в
целом. Здесь происходит лишь оптимизация скорости вычислений путем
кеширования (англ.
caching) промежуточных результатов.
Описанные действия
встречаются практически во многих блочных криптоалгоритмах и носят
название расширение ключа
(англ. key scheduling)
Назад | Содержание
| Вперед