2008 г.

Базы данных. Вводный курс

Сергей Кузнецов

7.2. Функциональные зависимости

Наиболее важные с практической точки зрения нормальные формы отношений основываются на фундаментальном в теории реляционных баз данных понятии функциональной зависимости. Для дальнейшего изложения нам потребуется несколько определений и утверждений (по ходу изложения мы будем пояснять их и иллюстрировать).

7.2.1. Общие определения

Пусть задана переменная отношения R, и X и Y являются произвольными подмножествами заголовка R («составными» атрибутами).

В значении переменной отношения R атрибут Y функционально зависит от атрибута X в том и только в том случае, если каждому значению X соответствует в точности одно значение Y. В этом случае говорят также, что атрибут X функционально определяет атрибут Y (X является детерминантом (определителем) для Y, а Y является зависимым от X). Будем обозначать это как R.XR.Y.

Для примера будем использовать отношение СЛУЖАЩИЕ_ПРОЕКТЫ {СЛУ_НОМ, СЛУ_ИМЯ, СЛУ_ЗАРП, ПРО_НОМ, ПРОЕКТ_РУК} (рис. 7.1). Очевидно, что если СЛУ_НОМ является первичным ключом отношения СЛУЖАЩИЕ, то для этого отношения справедлива функциональная зависимость (Functional Dependency – FD) СЛУ_НОМСЛУ_ИМЯ.

На самом деле, для тела отношения СЛУЖАЩИЕ_ПРОЕКТЫ в том виде, в котором оно показано на рис. 7.1, выполняются еще и следующие FD (1):

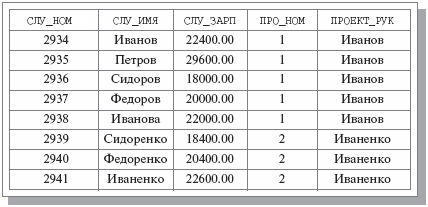
Рис. 7.1. Пример возможного тела отношения СЛУЖАЩИЕ_ПРОЕКТЫ

СЛУ_НОМСЛУ_ИМЯ
СЛУ_НОМСЛУ_ЗАРП
СЛУ_НОМПРО_НОМ
СЛУ_НОМПРОЕКТ_РУК
{СЛУ_НОМ, СЛУ_ИМЯ}СЛУ_ЗАРП
{СЛУ_НОМ, СЛУ_ИМЯ}ПРО_НОМ
{СЛУ_НОМ, СЛУ_ИМЯ}{СЛУ_ЗАРП, ПРО_НОМ}
…
ПРО_НОМПРОЕКТ_РУК и т.д.

Поскольку имена всех служащих различны, то выполняются и такие FD (2):

СЛУ_ИМЯСЛУ_НОМ
СЛУ_ИМЯСЛУ_ЗАРП
СЛУ_ИМЯПРО_НОМ и т.д.

Более того, для примера на рис. 7.1 выполняется и FD (3):

СЛУ_ЗАРППРО_НОМ

Однако заметим, что природа FD группы (1) отличается от природы FD групп (2) и (3). Логично предположить, что идентификационные номера служащих должны быть всегда различны, а у каждого проекта имеется только один руководитель. Поэтому FD группы (1) должны быть верны для любого допустимого значения переменной отношения СЛУЖАЩИЕ_ПРОЕКТЫ и могут рассматриваться как инварианты, или ограничения целостности этой переменной отношения.

FD группы (2) базируются на менее естественном предположении о том, что имена всех служащих различны. Это соответствует действительности для примера из рис. 7.1, но возможно, что с течением времени FD группы (2) не будут выполняться для какого-либо значения переменной отношения СЛУЖАЩИЕ_ПРОЕКТЫ.

Наконец, FD группы (3) основана на совсем неестественном предположении, что никакие двое служащих, участвующие в разных проектах, не получают одинаковую зарплату. Опять же, данное предположение верно для примера из рис. 7.1, но, скорее всего, это случайное совпадение.

В дальнейшем нас будут интересовать только те функциональные зависимости, которые должны выполняться для всех возможных значений переменных отношений.

Заметим, что если атрибут A отношения R является возможным ключом, то для любого атрибута B этого отношения всегда выполняется FD AB (в группе (1) к этим FD относятся все FD, детерминантом которых является СЛУ_НОМ). Обратите внимание, что наличие в отношении СЛУЖАЩИЕ_ПРОЕКТЫ FD ПРО_НОМПРОЕКТ_РУК приводит к некоторой избыточности этого отношения. Имя руководителя проекта является характеристикой проекта, а не служащего, но в нашем случае содержится в теле отношения столько раз, сколько служащих работает над проектом.

Итак, мы будем иметь дело с FD, которые выполняются для всех возможных состояний тела соответствующего отношения и могут рассматриваться как ограничения целостности. Как показывает (неполный) список (1), таких зависимостей может быть очень много. Поскольку они трактуются как ограничения целостности, за их соблюдением должна следить СУБД. Поэтому важно уметь сократить набор FD до минимума, поддержка которого гарантирует выполнение всех зависимостей. Мы займемся этим в следующих подразделах.

FD AB называется тривиальной, если AB (т. е. множество атрибутов A включает множество B или совпадает с множеством B).

Очевидно, что любая тривиальная FD всегда выполняется. Например, в отношении СЛУЖАЩИЕ_ПРОЕКТЫ всегда выполняется FD {СЛУ_ЗАРП, ПРО_НОМ}СЛУ_ЗАРП. Частным случаем тривиальной FD является AA.

Поскольку тривиальные FD выполняются всегда, их нельзя трактовать как ограничения целостности, и поэтому они не представляют интереса с практической точки зрения. Однако в теоретических рассуждениях их наличие необходимо учитывать.

7.2.2. Замыкание множества функциональных зависимостей. Аксиомы Армстронга. Замыкание множества атрибутов

Замыканием множества FD S является множество FD S⁺, включающее все FD, логически выводимые из FD множества S.

Для начала приведем два примера FD, из которых следуют (или выводятся) другие FD. Будем снова пользоваться отношением СЛУЖАЩИЕ_ПРОЕКТЫ. Для этого отношения выполняется, например, FD СЛУ_НОМ{СЛУ_ЗАРП, ОТД_НОМ}. Из этой FD выводятся FD СЛУ_НОМСЛУ_ЗАРП и СЛУ_НОМОТД_НОМ.

В отношении СЛУЖАЩИЕ_ПРОЕКТЫ имеется также пара FD СЛУ_НОМОТД_НОМ и ОТД_НОМПРОЕКТ_РУК. Из них выводится FD СЛУ_НОМПРОЕКТ_РУК. Заметим, что FD вида СЛУ_НОМПРОЕКТ_РУК называются транзитивными, поскольку ПРОЕКТ_РУК зависит от СЛУ_НОМ «транзитивно», через ПРО_НОМ.

FD AC называется транзитивной, если существует такой атрибут B, что имеются функциональные зависимости AB и BC и отсутствует функциональная зависимость CA.

Подход к решению проблемы поиска замыкания S⁺ множества FD S впервые предложил Вильям Армстронг²⁸⁾. Им был предложен набор правил вывода новых FD из существующих (эти правила обычно называют аксиомами Армстронга, хотя справедливость правил доказывается на основе определения FD). Обычно принято формулировать эти правила вывода в следующей форме. Пусть A, B и C являются (в общем случае, составными) атрибутами отношения R. Множества A, B и C могут иметь непустое пересечение. Для краткости будем обозначать через AB A UNION B. Тогда:

если BA, то AB (рефлексивность);
если AB, то ACBC (пополнение);
если AB и BC, то AC (транзитивность).

Истинность первой аксиомы Армстронга следует из того, что при BA FD AB является тривиальной.

Справедливость второй аксиомы докажем от противного. Предположим, что FD ACBC не соблюдается. Это означает, что в некотором допустимом теле отношения найдутся два кортежа t₁ и t₂, такие, что t₁ {AC} = t₂ {AC} (a), но t₁ {BC} t₂ {BC} (b) (здесь t {A} обозначает проекцию кортежа t на множество атрибутов A). По аксиоме рефлексивности из равенства (a) следует, что t₁ {A} = t₂ {A}. Поскольку имеется FD AB, должно соблюдаться равенство t₁ {B} = t₂ {B}. Тогда из неравенства (b) следует, что t₁ {C} t₂ {C}, что противоречит наличию тривиальной FD ACC. Следовательно, предположение об отсутствии FD ACBC не является верным, и справедливость второй аксиомы доказана.

Аналогично докажем истинность третьей аксиомы Армстронга. Предположим, что FD AC не соблюдается. Это означает, что в некотором допустимом теле отношения найдутся два кортежа t₁ и t₂, такие, что t₁ {A} = t₂ {A}, но t₁ {C} t₂ {C}. Но из наличия FD AB следует, что t₁ {B} = t₂ {B}, а потому из наличия FD BC следует, что t₁ {C} = t₂ {C}. Следовательно, предположение об отсутствии FD AC не является верным, и справедливость третьей аксиомы доказана.

Можно доказать, что система правил вывода Армстронга полна и совершенна (sound and complete) в том смысле, что для данного множества FD S любая FD, потенциально выводимая из S, может быть выведена на основе аксиом Армстронга, и применение этих аксиом не может привести к выводу лишней FD. Тем не менее Дейт по практическим соображениям предложил расширить базовый набор правил вывода еще пятью правилами:

AA (самодетерминированность) – прямо следует из правила (1);
если ABC, то AB и AC (декомпозиция) – из правила (1) следует, что BCB; по правилу (3) AB; аналогично, из BCС и правила (3) следует AC;
если AB и AC, то ABC (объединение) – из правила (2) следует, что AAB и ABBC; из правила (3) следует, что ABC;
если AB и CD, то ACBD (композиция) – из правила (2) следует, что AСBС и BCBD; из правила (3) следует, что ACBD;
если ABC и BD, то ABCD (накопление) – из правила (2) следует, что BСBCD; из правила (3) следует, что ABCD.

Пусть заданы отношение R, множество Z атрибутов этого отношения (подмножество заголовка R, или составной атрибут R) и некоторое множество FD S, выполняемых для R. Тогда замыканием Z над S называется наибольшее множество Z⁺ таких атрибутов Y отношения R, что FD ZY входит в S⁺.

Алгоритм вычисления Z⁺ очень прост. Один из его вариантов показан на рис. 7.2.

Рис. 7.2. Алгоритм построения замыкания атрибутов над заданным множеством FD

Докажем корректность алгоритма по индукции. На нулевом шаге Z[0] = Z, FD ZZ[I], очевидно, принадлежит S⁺ (тривиальная FD «выводится» из любого множества FD). Пусть для некоторого K выполняется FD ZZ[K], и пусть мы нашли в S такую FD AB, что AZ[K]. Тогда можно представить Z[K] в виде AC, и, следовательно, выполняется FD ZAC. Но по правилу (8) мы имеем FD ZACB, т.е. FD Z(Z[K] UNION B) входит во множество S⁺, что переводит нас на следующий шаг индукции.

Пусть для примера имеется отношение с заголовком {A, B, C, D, E, F} и заданным множеством FD S = {AD, ABE, BFE, CDF, EC}. Пусть требуется найти {AE}⁺ над S. На первом проходе тела цикла DO Z[1] равно AE. В теле цикла FOR EACH будут найдены FD AD и EC, и в конце цикла Z[1] станет равным ACDE. На втором проходе тела цикла DO при Z[2], равном ACDE, в теле цикла FOR EACH будет найдена FD CDF, и в конце цикла Z[2] станет равным ACDEF. Следующий проход тела цикла DO не изменит Z[3], и Z⁺ ({AE}⁺) будет равно ACDEF.

Алгоритм построения замыкания множества атрибутов Z над заданным множеством FD S помогает легко установить, входит ли заданная FD ZB в замыкание S⁺. Очевидно, что необходимым и достаточным условием для этого является BZ⁺, т. е. вхождение составного атрибута B в замыкание Z²⁹⁾.

Суперключом отношения R называется любое подмножество K заголовка R, включающее, по меньшей мере, хотя бы один возможный ключ R.

Одно из следствий этого определения состоит в том, что подмножество K заголовка отношения R является суперключом тогда и только тогда, когда для любого атрибута A (возможно, составного) заголовка отношения R выполняется FD KA. В терминах замыкания множества атрибутов K является суперключом тогда и только тогда, когда K⁺ совпадает с заголовком R.

28 К сожалению, классическая статья Армстронга – W.W. Armstrong. "Dependency Structures of Data Base Relationships", Proc. IFIP Congress, Stockholm, Sweden, 1974 – так и не переведена на русский язык (на самом деле, ее нелегко найти и в оригинале). Поэтому я не могу рекомендовать ее для дополнительного чтения, хотя обязан сослаться.

29 Мы используем здесь знаки операций проверки включения множеств, что не совсем корректно, поскольку если, например, множество B состоит из одного элемента, то для его обозначения используется имя соответствующего атрибута, и в этом случае правильнее было бы использовать знак «» (проверка вхождения элемента во множество).

Назад Содержание Вперёд