Методы бикластеризации для анализа интернет-данных

Дмитрий Игнатов,
кафедра анализа данных и искусственного интеллекта ГУ-ВШЭ

Назад Содержание Вперёд

3. Программные средства бикластеризации

Разработано довольно большое количество программных систем, которые можно отнести к программам бикластеризации. Как правило, такие системы служат нуждам какой-либо конкретной области, и методы бикластеризации являются одним из инструментов, доступных аналитику наряду с традиционными методами анализа данных (например, кластеризацией). В этой части работы мы не будем детально описывать каждую из рассматриваемых систем, и приведенный их перечень будет далеко не полным.

Суть в том, что для каждой области применения мы укажем хотя бы одно из такое средство и кратко опишем его возможности. Основными областями применения в нашем рассмотрении являются биоинформатика (генетические данные), Data Mining, Формальный Анализ Понятий, социальные сети, графовая и спектральная кластеризация.

3.1. Система бикластеризации генетических данных BicAT

Опишем систему BicAT, разработанную швейцарскими учеными, которые специализируются в области биоинформатики и анализа генетических данных. Отметим также, что данное программное обеспечение свободно распространяется.

В системе BicAT реализованы следующие методы бикластеризации:

• алгоритм Ченга и Черча (CC), в котором используется величина среднеквадратичного остатка [25];
• алгоритм итеративной сигнатуры (the Iterative Signature Algorithm, ISA), в котором ищутся подматрицы, представляющие собой неподвижные точки [43];
• алгоритм, сохраняющий порядок на подматрицах (the Order-Preserving Submatrix Algorithm, OPSM) и обнаруживающий большие подматрицы, для которых линейный порядок, заданный на столбцах, выполняется на всех строках [16];
• алгоритм xMotifs — итеративный метод, отыскивающий бикластеры с квази-постоянными значениями выражений [58];
• Bimax — точный алгоритм бикластеризации, основанный на стратегии "разделяй и властвуй", которая приспособлена для нахождения всех максимальных биклик в соответствующем графовом представлении матрицы [60].

Дополнительно реализованы две стандартных процедуры кластеризации, а именно, иерархическая кластеризация и метод K-средних.

Кратко опишем основные функции и возможности системы бикластеризации BicAT.

Матрица исходных данных отображается в главном окне системы в виде так называемой тепловой карты (меньшим значениям степени проявления генов соответствует зеленый цвет, большим — красный). К средствам предобработки данных, реализованным в системе, можно отнести нормализацию, дискретизацию и логарифмирование входных значений. Подобные процедуры необходимы для адекватной работы методов; например, метод Bimax принимает в качестве входных данных только двоичные матрицы, а следовательно, бинарная дискретизация значений необходима.

Результаты работы каждого метода отображаются в виде древесной структуры в левой области главного окна системы. Там же отображаются узлы дерева, соответствующие исходным наборам данных и результатам предобработки. Для каждого из методов бикластеризации можно задать специфические параметры, например, число кластеров для метода CC или ограничения на размер бикластера для метода Bimax.

В системе реализованы средства поиска бикластеров по имени гена и/или признака, а также механизм фильтрации результатов бикластеризации по размеру бикластеров (сверху и снизу) и степени их перекрытия. Помимо таких, очевидно, необходимых средств постобработки, в системе реализован метод парного анализа генов (Gene Pair Analysis), позволяющий исследовать совстречаемость пар генов.

В системе приняты соглашения об именовании наборов данных и результатов анализа, существует возможность их экспорта в текстовый формат.

3.2. Программные средства сообщества ФАП

Среди программных средств в области ФАП отметим только три наиболее часто используемые исследователями программы, находящиеся в свободном доступе: Concept Explorer [2], ToscanaJ [39] и Galicia [80]. Кратко опишем их назначение и возможности.

Все они пригодны для построения решеток понятий и отображения их диаграмм. Отличительными особенностями ConceptExplorer являются удобный интерфейс, наличие нескольких способов рисования диаграммы решетки, а также поиск базиса импликаций и ассоциативных правил. Помимо этого, ConExp поддерживает исследование признаков — интерактивную процедуру приобретения знаний.

Программа ToscanaJ позволяет строить вложенные диаграммы решеток понятий, шкалировать признаки в смысле ФАП, устанавливать связь с базами данных и предоставляет некоторые возможности, учитывающие динамику решеток.

Программа Galicia не отличается удобным интерфейсом, но предоставляет массу возможностей, а именно, позволяет шкалировать признаки,строить решетки-айсберги, находить базис импликаций, множество генераторов для данного понятия и отображать трехмерную диаграмму решетки понятий.

3.3. Система Coron для Data Mining

Система анализа данных Coron [74] предназначена для поиска частых множеств признаков и ассоциативных правил. Следует особо отметить, что данный продукт является результатом диссертационной работы Ласло Затмари.

Программа обладает неплохим графическим интерфейсом, собственным форматом данных, возможностью работы с базами данных. Для поиска частых множеств признаков используются наиболее эффективные алгоритмы сообщества FIM, а также алгоритмы, разработанные самим автором [75]. Поиск ассоциативных правил также использует эффективные алгоритмы, опирающиеся на достижения ФАП и оказавшиеся полезными для компактного представления правил и построения их базисов. Еще одним достоинством продукта является свободный доступ и кроссплатформенность (в смысле технологии Java).

3.4. Другие системы бикластеризации

Стоит отдельно упомянуть системы бикластеризации на графах и спектральной кластеризации. Система CLUTO [71,87] — библиотека алгоритмов для кластеризации как данных небольшой размерности, так и многомерных, а также анализа свойств различных кластеров. Авторы рекомендуют использовать CLUTO для кластеризации данных во многих областях, таких как информационный поиск, базы данных транзакций, Интернет и биология. В программе реализована кластеризация на графах, различные меры сходства, поддерживается поиск клик графа и частых множеств признаков, реализованы удобные средства визуализации gCluto [62].Отличительная особенность программы заключается в возможности анализа больших массивов, содержащих сотни тысяч объектов и десятки тысяч признаков.

Две других системы предназначенные для графовой кластеризации — это Chaco [41] и METIS [11]. Укажем, что Metis отличается высокой скоростью вычислений для больших массивов данных, а в Chaco реализована спектральная кластеризация на графах. Не будем подробно их описывать, но укажем на то, что поиск клик и их различных ослаблений в двудольном графе (в том числе и взвешенном) сводится к постановкам задач бикластерзации. А это означает, что такие системы можно рассматривать как системы бикластеризации.

4. Прикладные задачи

4.1. Приложения в биологии: анализ генетических данных

Как уже было указано в разделе 1.1, задача бикластеризации в последние годы приобрела большую популярность в связи с растущей потребностью в анализе генетических данных. Почти каждая работа в этой области, описывающая новый алгоритм бикластеризации, содержит раздел посвященный экспериментам на реальных данных.

Приведем несколько примеров. Ченг и Черч в работе [25] применяют бикластеризацию к двум матрицам генной экспрессии, а именно, к данным, описывающим клетки дрожжей (Yeast Saccharomyces Cerevisiae) для 2884 генов и 17 условий, и к данным о B-клетках человека (B-cells) для 4026 генов и 96 условий. Танг и др. [78] применяют алгоритм ITWC к данным генной экспрессии с 4132 генами и 48 примерами пациентов множественного склероза, а Бен-Дор и др. [16] используют данные о раке груди для 3226 генов при 22 различных экспериментальных условиях.

Напомним, что основная задача такого анализа — выявление групп генов, проявляющих сходное поведение только при определенных условиях. В дальнейшем специалист генетик на основании проведенного анализа выдвигает гипотезу о том, является ли данная группа генов причиной исследуемой болезни.

Помимо данных генной экспрессии, в качестве приложений в биологии можно привести пример из работы Лиу и Ванга [53], которые анализировали активность лекарственных препаратов на матрице из 10000 строк и 30 столбцов, в которой каждой строке соответствовало химическое вещество, а столбцы представляли его признаки.

В сообществе рассматриваются и другие массивы генетических данных, в основном относящихся к раковым заболеваниям, таким как лимфома.

4.2. Информационный поиск (Information Retrieval): бикластеризация документов

В задачах информационного поиска и анализа текстов (text mining) бикластеризация применяется для обнаружения кластеров документов, обладающих сходными свойствами только по нескольким признакам, таким как слова и изображения. Такая информация очень важна для запросов и индексации поисковых интернет-систем. Диллон в своей работе [29] использует бикластеризацию для одновременного группирования документов и слов. Исходные данные представляют собой матрицу F, в которой строки отвечают словам, а столбцы — документам, а ненулевой элемент показывает присутствие слова 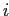в документе : , где показывает число вхождений слова 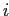в документ , — общее число документов, а — число документов, содержащих слово 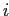. Такую матрицу принято называть матрицей инциденций, а вместо термина бикластеризация использовать кокластеризация (co-clustering).

Проблемы кластеризации документов и слов в отдельности хорошо изучены в контексте информационного поиска и анализа текстов. Однако кластеризации лишь по одному измерению оказывается недостаточно. Допустим, имеется коллекция документов никак не сгруппированных. Тогда кластеризация помогает организовать коллекцию для целей дальнейшей навигации и поиска. Слова могут быть кластеризованы на основе документов в которых они встречаются. Кластеры слов полезны для автоматического построения статистических тезаурусов, уточнения запросов и автоматической классификации документов.

В этой работе Диллон пытается выявить подмножества слов и документов, сильно связанных друг с другом. В его модели, как и в работе Танай и др.[76], матрице исходных данных сопоставляется двудольный граф, и автор использует спектральный подход, похожий на предложенный Клугер и др. [45]. Эксперименты проводятся на трех коллекциях документов: Medline (1033 медицинских статьи), Cranfield (1400 статей про системы аэронавтики) и Cisi (1460 статьи по информационному поиску). Другие примеры бикластеризации для этого типа матриц можно найти в работе Диллона [30].

Для задачи выявления документов-дубликатов было предпринято две относительно успешные попытки использования ФАП и частых замкнутых множеств признаков (см. работы Кузнецова и Игнатова [6,3] и более позднюю статью другого исследователя [38]). Подробное описание постановки задачи, вычислительной модели см. в разделе 4.1.

4.3. Социальные сети: выявление сообществ

В последние годы возобновился интерес к междисциплинарным исследованиям в области анализа социальных сетей, в которых задействованы математическая социология и информатика, опирающиеся на аппарат теории графов. Усилия в этом направлении в значительной степени поддерживаются благодаря новым вычислительным возможностям и доступности электронных данных для некоторых социальных систем: сообществ ученых, людей, ведущих личные электронные дневники (weblogers), покупателей интернет-магазинов, сетей друзей, сайтов знакомств и так далее.

В частности, в центре многих текущих исследований находятся сети знаний, т.е. сети взаимодействий, в которых агенты производят знания или обмениваются ими. В число исследований входит выявление сообществ, рассматриваемое как нахождение агентов, которые обладают множеством общих признаков. Анализ социальных сетей специализируется на методах выявления, описания и правдоподобной организации различных видов социальных сообществ. Для анализа социальных аспектов сообществ основной интерес представляют лидеры, периферийные члены, межгрупповое и внутригрупповое взаимодействие.

Решетки понятий, которые мы рассматриваем как способ бикластерзации, успешно применялись для анализа эпистемических сообществ [65,63] (т.е. агентов, имеющих дело с одинаковыми темами, например, научные сообщества или пользователи блогов) или филиальных сетей (акторы принадлежат одной и той же организации). Успех этого подхода обусловлен наличием таксономий бикластеров, что оказывается полезным при иерархическом описании групп акторов в терминах сходства интересов.

Отметим ключевые работы, которые способствовали росту интереса к исследованиям в этой области. В начале 90-х известный американский социолог Линтон Фриман стал применять решетки понятий в контексте социальных исследований [32], другой важной фигурой является французский исследователь Винсент Дюкен [82]. Часть работ, в которых используется ФАП, связана с исследованием веб-сообществ, например, статья [64]. С применением ФАП проводились также исследования посещаемости сайтов, а именно, выполнялось построение таксономий групп посетителей, см. работы Кузнецова и Игнатова [50] и Кедрова и Кузнецова [4]. Более подробно постановка задачи исследования посещаемости сайтов и пути ее решения обсуждаются в разделе 4.2.

4.4. Интернет-приложения: e-commerce, recommendation systems, collaborative filtering, target marketing

Методы бикластеризации могут быть использованы для так называемой коллаборативной фильтрации (collaborative filtering) при обнаружении групп покупателей со сходными предпочтениями в виде некого подмножества товаров (задача целевого маркетинга). Похожая ситуация имеет место в рекомендательных системах, где бикластеры предоставляют информацию о сходных интересах групп посетителей.

Необходимо отметить, что рекомендательные системы и целевой маркетинг — важные приложения в области электронной коммерции (см., например, [12]). В таких приложениях основной целью является обнаружение групп покупателей, ведущих себя похожим образом, чтобы предсказать их интересы и предложить адекватные рекомендации. Отметим несколько работ, освещающих вопросы применения методов бикластеризации к таким данным.

Джионг Янг и др. [84,85] использовали для проведения экспериментов массив данных MovieLens, собранный исследовательской группой GroupLens университета Миннесоты. Массив данных представляет собой матрицу, строки которой описывают 943 покупателя, а столбцы — 1682 фильма. Значения матрицы — целые числа от 1 до 10, они представляют рейтинг, который покупатель присвоил фильму. Матрица довольно разреженная, т.к. покупатель оценивает в среднем менее 10% фильмов. Хайксун Янг и др. [81] также провели эксперименты на этих данных.

Хоффман и Пузича [42] применяли бикластеризацию для коллаборативной фильтрации на массиве EachMovie, который состоит из данных, собранных в Интернете для почти трех миллионов предпочтений с оценками от 0 до 5. Унгар и Фостер [79] также используют данные о фильмах, в которых учитывается лишь факт просмотра фильма, поэтому анализируемая матрица — бинарная.

Другим примером является рынок Интернет-рекламы, для которого актуален поиск бикластеров, представляющих отдельные рынки, т.е. множества покупателей и приобретаемых ими рекламных словосочетаний (см. [88]). Решение аналогичной задачи описывается и в данной работе (см. раздел 5.3).

4.5. Бикластеризация электоральных данных

Существуют и менее распространенные приложения бикластеризации, опирающиеся, например, на данные о голосовании. В этом случае необходимо выявлять подмножества строк избирателей, придерживающихся похожих политических взглядов и проявляющих сходное электоральное поведение на подмножестве рассматриваемых признаков.

Хартиган [37] применял бикластеризацию для двух массивов данных. Первый массив — данные о голосовании на президентских выборах США, отражающие процент голосов, которые были отданы за республиканцев в южных штатах в период с 1900 г. по 1968 г. Второй массив данных о голосовании в ООН в 1969 г. и 1970 г. В первом случае матрица состоит из множества строк, представляющих штаты, и множества столбцов, соответствующих годам. Каждое значение представляет процент голосов штата 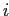в году .

Бикластер в этом случае — это подмножество штатов со сходными результатами голосования на подмножестве годов. Для второго набора строки соответствуют странам, а столбцы — предложениям по обсуждаемым вопросам. Бикластером является множество стран со сходными голосами на подмножестве обсуждаемых предложений.

5. Эксперименты на массивах Интернет-данных

5.1. Поиск сходства Интернет-документов с помощью частых замкнутых множеств признаков.

У множества документов в Интернете имеются дубликаты, в связи с чем необходимы средства эффективного вычисления кластеров документов-дубликатов [20, 21, 22, 26, 27, 40, 44, 46, 70, 61]. В этом разделе описываются исследования, посвященные применению алгоритмов Data Mining для поиска кластеров дубликатов с использованием синтаксических и лексических методов составления образов документов. На основе экспериментов делаются некоторые выводы о способе выбора параметров методов.

Постановка задачи

У огромного числа документов (по некоторым источникам до 30%) в Интернете имеются дубликаты, и поисковые машины должны обладать эффективными средствами вычисления кластеров дубликатов. Происхождение дубликатов может быть разным — от дублирования компаниями собственной информации на разных серверах (создание зеркал) до злонамеренных — обмана программ индексаторов веб-сайтов, незаконного копирования и спамерских рассылок.

Обычно дубликаты документов определяются на основе отношения сходства на парах документах: два документа сходны, если некоторая числовая мера их сходства превышает некоторый порог [20]. По отношению сходства вычисляются кластеры сходных документов, например, по транзитивному замыканию отношения сходства [20]. Вначале, после снятия HTML-разметки документы, как линейные последовательности слов (символов), преобразуются во множества. Здесь двумя основными схемами (определяющими весь возможный спектр смешанных методов) являются синтаксические и лексические методы. К синтаксическим относится метод шинглирования [22], в котором документ в итоге представляется набором хеш-кодов; этот метод испоьзовался в поисковых системах Google и AltaVista. В лексических методах [44] большое внимание уделяется построению словаря — набора дескриптивных слов; известны его разновидности, такие I-match и метод ключевых слов Ильинского [44].

На втором этапе из документа, представленного множеством синтаксических или лексических признаков, выбирается подмножество признаков, образующее краткое описание (образ) документа. На третьем этапе определяется отношение сходства на документах с помощью некоторой метрики сходства, сопоставляющей двум документам число в интервале [0, 1], и некоторого параметра — порога, выше которого находятся документы-дубликаты.

На основе отношения сходства документы объединяются в кластеры (полу-)дубликатов. Определение кластера также может варьироваться. Одно из возможных определений, часто используемых на практике (например, в компании AltaVista), но наиболее слабых, упоминается в обзоре [20]: если документам Интернета сопоставить граф, вершины которого соответствуют самим документам, а ребра — отношению «быть (почти) дубликатом», то кластером объявляется компонента связности такого графа. Достоинством такого определения является эффективность вычислений. Недостаток такого подхода очевиден: отношение «быть (почти) дубликатом» не является транзитивным, поэтому в кластер сходных документов могут попасть абсолютно разные документы.

В качестве противоположного — «самого сильного» — определения кластера, опирающимся на отношение «быть (почти) дубликатом», можно принять клики графа. При этом каждый документ из кластера должен быть сходным со всеми другими документами того же кластера. Такое определение кластера более адекватно передает представление о групповом сходстве, но, к сожалению, практически не применимо в масштабе Интернета, поскольку поиск клик в графе — классическая труднорешаемая задача.

Исходя из предложенных формулировок, можно было бы находить необходимый баланс между соответствием определения кластеров множествам «в самом деле» сходных документов и сложностью вычисления кластеров. Здесь мы рассматриваем сходство не как отношение на множестве документов, а как операцию, сопоставляющую двум документам множество общих элементов их сокращенных описаний, где в качестве элементов описания выступают либо синтаксические, либо лексические единицы. Кластер дубликатов определяется как множество документов, у которых число общих элементов описания превышает определенный порог.

Приводятся результаты экспериментальной проверки данного метода на основе сравнения результатов его применения (для разных значений порогов) со списком дубликатов, составленным на основе результатов применения других методов к тому же множеству документов. Исследовалось влияние на результат следующих параметров модели: использование синтаксических или лексических методов представления документов, использование методов «n минимальных элементов в перестановке» и «минимальные элементы в n перестановках» [20], параметры шинглирования, величина порога сходства образов документов. Одна из задач проекта заключалась в том, чтобы связать вычисление попарного сходства образов документов с построением кластеров документов, чтобы, с одной стороны, получаемые кластеры были бы независимы от порядка рассмотрения документов (в отличие от методов кластерного анализа), а с другой стороны гарантировали бы наличие реального попарного сходства всех образов документов в кластере.

Описание вычислительной модели

В качестве методов представления документов (создания образа документа) использовались стандартные синтаксические и лексические подходы с разными параметрами.

В рамках синтаксического подхода была реализована схема шинглирования и составление краткого образа (скетча) документов на основе методов «n минимальных элементов в перестановке» и «минимальные элементы в n перестановках», описание которых можно найти, например, в [21, 22].

Программа shingle с двумя параметрами length и offset порождает для каждого текста набор последовательностей слов (шинглов) длины length, так что отступ от начала одной последовательности до начала другой последовательности в тексте имеет размер offset. Полученное таким образом множество последовательностей хэшируется, так что каждая последовательность получает свой хэш-код.

Далее из множества хэш-кодов, соответствующему документу, выбирается подмножество фиксированного (с помощью параметра) размера с использованием случайных перестановок, описанных в работах [20, 21, 22]. При этом вероятность того, что минимальные элементы в перестановках хэш-кодов на множествах шинглов документов A и B (эти множества обозначаются через и соответственно) совпадут, равна мере сходства этих документов sim(A,B):

Основные определения, связанные с частыми замкнутыми множествами, естественно, даются в терминах анализа формальных понятий (ФАП) [33]. Мы рассматриваем формальный контекст , где D — множество документов, а F — множество хеш-кодов (fingerprins), отношение 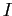показывает, что некий объект обладает признаком в том и только том случае, когда . Для множества документов множество их общих признаков служит описанием их сходства, а замкнутое множество является кластером сходных объектов (с множеством общих признаков ). Для произвольного величина является поддержкой B и обозначается supp(B).

Нетрудно видеть, что множество 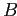замкнуто тогда и только тогда, когда для любого имеет место . Именно это свойство используется для определения замкнутости в методах Data Mining. Множество 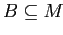называется 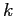-частым, если (то есть множество признаков B встречается в более чем 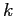объектах), где 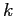— параметр.

Вычисление частых замкнутых множеств признаков (содержаний) приобрело важность в Data Mining благодаря тому, что по этим множествам эффективно вычисляются множества всех ассоциативных правил [59]. Фактически, мы будем вычислять частные замкнутые множества признаков для контекста, дуального к , т.е. находить такие множества документов-признаков контекста , для которых размер множества их общих шинглов превышает заданный порог сходства.

Хотя теоретически размер множества всех замкнутых множеств признаков (содержаний) может быть экспоненциальным относительно числа признаков, на практике таблицы данных сильно "разрежены" (то есть среднее число признаков на один объект весьма мало), и число замкнутых множеств невелико. Для таких случаев существуют весьма эффективные алгоритмы построения всех наиболее частых замкнутых множеств признаков (см. также обзор по алгоритмам построения всех замкнутых множеств [47]).

В последние годы проводился ряд соревнований по быстродействию таких алгоритмов на серии международных семинаров под общим названием FIMI (Frequent Itemset Mining Implementations). Пока лидером по быстродействию считается алгоритм FPmax* [35], показавший наилучшие результаты по быстродействию в соревновании 2003 года. Мы использовали этот алгоритм для построения сходства документов и кластеров сходных документов. При этом в роли объектов выступали элементы описания (шинглы или слова), а в роли признаков — документы. Для такого представления «частыми замкнутыми множествами» являются замкнутые множества документов, для которых число общих единиц описания в образах документов превышает заданный порог.

Программная реализация и компьютерные эксперименты

Программные средства для проведения экспериментов в случае синтаксических методов включали следующие блоки:

1. парсер формата XML для коллекции ROMIP;
2. снятие html-разметки;
3. нарезка шинглов с заданными параметрами;
4. хэширование шинглов;
5. составление образа документов путем выбора подмножества (хэш-кодов) шинглов с помощью методов «n минимальных элементов в перестановке» и «минимальные элементы n n перестановках»;
6. cоставление по результатам методов 4-5 инвертированной таблицы «список идентификаторов документов—шингл» — подготовка данных к формату программ вычисления замкнутых множеств;
7. вычисление частых замкнутых множеств с заданным порогом общего числа документов, в которое входит данное множество шинглов: программа MyFim (реализующая алгоритм FPmax*);
8. сравнение со списком дубликатов РОМИП – программа Comparator.

В качестве экспериментального материала нами использовалась URL-коллекция РОМИП, состоящая из 52 файлов общего размера 4,04 Гб. Для проведения экспериментов коллекция разбивалась на несколько частей, включающих от трех до двадцати четырех файлов (приблизительно от 5% до 50% от размера всей коллекции).

В экспериментах использовались следующие пПараметры шинглирования: число слов в шингле 10 и 20, отступ между началом соседних шинглов 1. Данное значение отступа означает, что начальное множество шинглов включало все возможные последовательности цепочек слов.

Эксперименты проводились на персональном компьютере P-IV HT с тактовой частотой 3.0 ГГц, оперативной памятью объемом в 1024 Мб и операционной системой Windows XP Professional. Результаты экспериментов и время, затраченное на их проведение, частично приводятся в следующих таблицах и рисунках.

(1) Результаты работы метода “ минимальных элементов в перестановке”

(2) Результаты работы метода “минимальные элементы в n перестановках”.

(3) Вычисление образов документов для методов " минимальных элементов в перестановке" и метода "минимальные элементы в перестановках".

(3) Время работы FPmax* для метода “ минимальных элементов в перестановке”.

(4) Время работы FPmax* для метода “минимальные элементы в перестановках”.

Наклон верхней линии при учете логарифмического масштаба диаграмм напоминает о том, что теоретическая временная сложность (в худшем случае) работы алгоритма экспоненциальна.

(5) Сравнение эффективности алгоритмов поиска максимальных замкнутых множеств.

По диаграмме видно, что наилучшие результаты показали алгоритмы Fpmax* и Afopt. А алгоритм AddIntent* из сообщества FCA-алгоритмов даже превзошел Mafia из FIMI, что является неплохим результатом для, как правило, более ресурсоемких алгоритмов первой группы.

Выводы и направление дальнейшей работы

По результатам наших экспериментов по использованию методов порождения частых замкнутых множеств в сочетании с традиционными синтаксическими и лексическими средствами можно сделать следующие выводы.

• Методы порождения частых замкнутых множеств представляют эффективный способ определения сходства документов одновременно с порождением кластеров сходных документов.
• На результаты синтаксических методов определения дубликатов значительное влияние оказывает параметр «длина шингла». Так, в наших экспериментах результаты для длины шингла, равной 10, были существенно ближе к списку дублей РОМИП, чем для длины шингла, равной 20, 15 и 5.
• В экспериментах для всех значений параметров не было обнаружено существенного влияния использования метода «минимальные элементы в n перестановках» на качество результатов. По-видимому, на практике достаточно случайности, задаваемой отбором шинглов с помощью метода «n минимальных элементов в перестановке».

  Необходимы дальнейшие эксперименты с использованием различных значений параметров синтаксических методов и сравнение результатов с результатами применения лексических методов, в которых используются инвертированные индексы коллекций. Необходимо сравнение методов кластеризации, в которых применяются замкнутые множества признаков, с алгоритмами, основанными на поиске минимальных разрезов вершин (cut) в двудольных графах, в которых множества вершин соответствуют множествам документов и множествам признаков [29, 87]. Эти методы родственны, поскольку замкнутые множества документов естественным образом выражаются через минимальные разрезы такого рода двудольных графов.

Назад Содержание Вперёд