2008 г.
Методы бикластеризации для анализа интернет-данных
Дмитрий Игнатов,
кафедра анализа данных и искусственного интеллекта ГУ-ВШЭ
Назад Содержание Вперёд
2.4. Аддитивная бокс-кластеризация
В работе [56] предложена модель аддитивной кластеризации для решения проблемы бикластеризации. Помимо прочего, данная работа интересна тем, что в ней приведена обширная библиография по моделям и методам бимодальной кластеризации (two-mode clustering), которая охватывает период с 1972 по 1993. В основу подхода автор положил модель аддитивной кластеризации ([69],[55]) и адаптировал ее для бимодальных данных (например, объектно-признаковых).
В ключевой статье [56] обсуждается еще один схожий подход ошибки дисперсии (error-variance approach), предложенный в [31], проводится сравнение с ним, показано как с помощью модели аддитивной бокс-кластеризации можно преодолеть проблемы, возникающие при его использовании. Первая проблема заключается в выборе "стандартного" значения близости, используемого при построении кластеров, а вторая — в возможности выявления перекрывающихся кластеров. Помимо преодоления этих недостатков, кстати, отмеченных авторами этого метода, в модели аддитивной бокс-кластеризации оценивается вклад каждого кластера в общую сумму квадратов входных данных.
2.4.1. Описание модели
Исходные данные в модели представлены матрицей
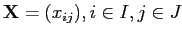 ,
где
,
где 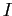 и
и 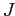 — множества индексов соответствующие двум типам величин и
— множества индексов соответствующие двум типам величин и 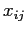 — бимодальные значения близости, рассматриваемые как сходство. Задача аналитика — выявить основные связи между членами этих двух множеств, представленными значениями
— бимодальные значения близости, рассматриваемые как сходство. Задача аналитика — выявить основные связи между членами этих двух множеств, представленными значениями 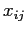 .
Для этой цели используется понятие бимодального кластера или бокс-кластера. Бокс-кластер определяется как Декартово произведение
.
Для этой цели используется понятие бимодального кластера или бокс-кластера. Бокс-кластер определяется как Декартово произведение
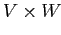 подмножеств
подмножеств
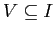 и
и
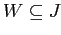 .
Любой бокс-кластер связан с подматрицей
.
Любой бокс-кластер связан с подматрицей
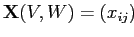 .
.
Рассмотрим множество из 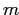 бокс-кластеров
бокс-кластеров
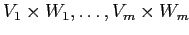 с соответствующими весами интенсивности
с соответствующими весами интенсивности
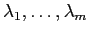 .
Будем называть такие кластеры аддитивными бокс-кластерами, если они приближают входные данные
.
Будем называть такие кластеры аддитивными бокс-кластерами, если они приближают входные данные
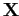 в соответствии со следующей моделью (сравните [69],[55]):
в соответствии со следующей моделью (сравните [69],[55]):
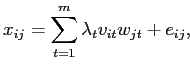 |
(2.3) |
с "небольшими" по величине остатками 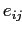 ,
,
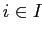 ,
,
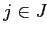 .
Булевы векторы
.
Булевы векторы
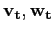 соответствуют бокс-кластеру
соответствуют бокс-кластеру
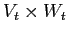 по следующему правилу:
по следующему правилу: 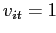 тогда и только тогда, когда
тогда и только тогда, когда 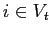 ,
и
,
и 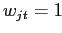 тогда и только тогда, когда
тогда и только тогда, когда
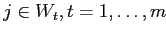 .
.
Аддитивная кластеризация использует двойную жадную стратегию оптимизации:
- кластеры находятся последовательно;
- каждый кластер формируется инкрементально поэлементным добавлением.
В частности, вначале находим только один бокс-кластер
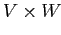 ,
который минимизирует следующий критерий наименьших квадратов, основанный на модели (2.3):
,
который минимизирует следующий критерий наименьших квадратов, основанный на модели (2.3):
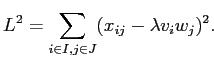 |
(2.4) |
Для любого 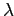 (например, равного максимальному
(например, равного максимальному 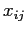 или среднему по всей подматрице
или среднему по всей подматрице
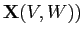 критерий (2.4) может быть записан следующим образом:
критерий (2.4) может быть записан следующим образом:
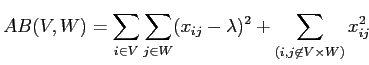 . . |
(2.5) |
Данный критерий выражает идею близости элементов подматрицы 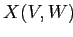 к одному и тому же значению
к одному и тому же значению 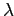 .
Одно из преимуществ критерия (2.5) заключается в его немонотонности в традиционном понимании качества подгонки. Рассмотрим, например, его изменение, когда
.
Одно из преимуществ критерия (2.5) заключается в его немонотонности в традиционном понимании качества подгонки. Рассмотрим, например, его изменение, когда
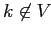 добавляется к
добавляется к 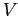 :
:
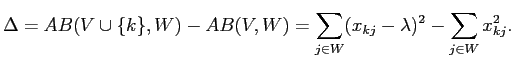 |
(2.6) |
Значение разности может быть либо отрицательным, либо положительным в зависимости от близости подмножества из строки 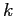 ,
соответствующего
,
соответствующего 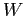 ,
к
,
к 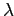 или 0.
Если
или 0.
Если 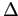 отрицательно, то
отрицательно, то 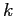 должно быть добавлено к
должно быть добавлено к 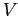 ,
так как это уменьшает значение критерия
,
так как это уменьшает значение критерия 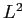 в (2.4). Если
в (2.4). Если 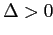 ,
то
,
то 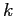 не добавляется к
не добавляется к 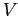 ,
потому что значение
,
потому что значение 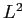 возрастет. Знак
возрастет. Знак 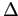 не зависит от действий на предыдущих шагах, что влечет естественное условие прекращения добавления элементов — изменение
не зависит от действий на предыдущих шагах, что влечет естественное условие прекращения добавления элементов — изменение 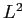 становится положительным для любой внешней строки
становится положительным для любой внешней строки 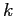 (или столбца
(или столбца 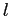 ).
).
Рассмотрим критерий аддитивной кластеризации (2.4) более подробно. Очевидно, что (2.5) можно переписать следующим образом.
В последнем выражении первое слагаемое — постоянная величена; раскрывая скобки под знаком суммирования во втором слагаемом приходим к новой записи критерия (2.5). Критерий (2.5) представляет собой разность постоянного члена
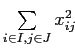 и
и
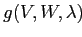 ,
где
,
где
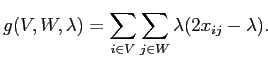 |
(2.7) |
Теперь для минимизации критерия (2.5) необходимо максимизировать (2.7). Критерий (2.7) позволяет лучше интерпретировать условие оптимальности, основанное на изменении знака (2.6) с отрицательного на положительный, когда
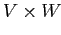 оптимально. В самом деле, приращение (2.7), когда
оптимально. В самом деле, приращение (2.7), когда 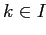 добавляется к
добавляется к 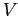 (
(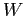 остается без изменений), равно:
остается без изменений), равно:
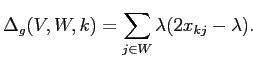 |
(2.8) |
Для простоты положим, что 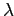 положительно. В этом случае
положительно. В этом случае
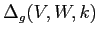 будет отрицательным, когда среднее значение
будет отрицательным, когда среднее значение
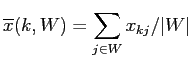 |
(2.9) |
меньше, чем 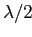 .
Аналогичное условие выполняется для столбцов и определяется симметричным образом. Становится очевидным, что означает выбор максимального значения
.
Аналогичное условие выполняется для столбцов и определяется симметричным образом. Становится очевидным, что означает выбор максимального значения 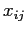 в качестве
в качестве 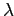 ,
как, например, в модели [31]. Бокс-кластер
,
как, например, в модели [31]. Бокс-кластер
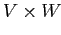 должен включать только те объекты
должен включать только те объекты 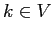 и
и 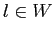 ,
для которых среднее сходство (average proximity)
,
для которых среднее сходство (average proximity)
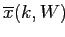 (см. (2.9)) и
(см. (2.9)) и
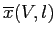 не меньше половины максимального значения. Такой выбор
не меньше половины максимального значения. Такой выбор 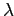 приводит к обнаружению бокс-кластеров с большими внутренними значениями сходства.
Оптимальное значение
приводит к обнаружению бокс-кластеров с большими внутренними значениями сходства.
Оптимальное значение 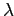 ,
минимизирующее критерий (2.4) для данного бокс-кластера
,
минимизирующее критерий (2.4) для данного бокс-кластера
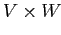 ,
равно среднему внутреннему сходству
,
равно среднему внутреннему сходству
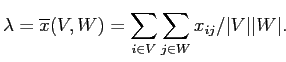 |
(2.10) |
Для оптимального значения 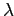 из (2.10) при его подстановке в критерий
из (2.10) при его подстановке в критерий
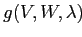 из (2.7) получим
из (2.7) получим
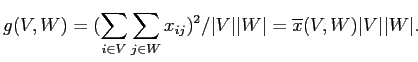 |
(2.11) |
Как видим, эта форма критерия (2.7) не содержит 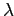 (определенного по формуле (2.10) ) и может быть легко преобразована для случая, когда оптимальное значение
(определенного по формуле (2.10) ) и может быть легко преобразована для случая, когда оптимальное значение 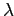 отрицательно.
отрицательно.
Назад Содержание Вперёд