Методы бикластеризации для анализа интернет-данных
Дмитрий Игнатов,
кафедра анализа данных и искусственного интеллекта ГУ-ВШЭ
2.2. Алгоритм BiMax
В обзоре [13] проводится систематическое сравнение пяти алгоритмов бикластеризации с предложенным авторами методом BiMax. И хотя каждый из алгоритмов взятых для сравнения придерживается своей собственной вычислительной модели, авторы обзора используют их только для анализа 0/1 данных. Преобразование значений в исходных наборах данных генной экспрессии к бинарным происходит путем нормализации их логарифмов и последующей дискретизации.
2.2.1. Описание модели
Вычислительная модель предполагает, что существует только два возможных уровня генной экспрессии: изменение и отсутствие изменения для данного эксперимента. Множество из m экспериментов для n генов может быть представлено бинарной матрицей
, где ячейк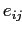а 
равна 
, если ген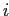 
проявился для условия 
, иначе 0.
Бикластер 
соответствует подмножеству генов
,
которые проявились для всего подмножества условий
.
Другими словами, пара
определяет подматрицу E для которой все элементы равны 1. Отметим, что согласно такому определению каждая ячейка ,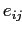
имеющая значение 1, является бикластером. Однако такие кластеры тривиальны и не представляют особого интереса, поэтому мы рассматриваем только максимальные по вложению бикластеры, т.е. не содержащиеся ни в одном другом.
Пара
называется максимальным по вложению бикластером тогда и только тогда, когда (1)
и (2)
такой, что (a)
и (b)
.
Отметим, что такие максимальные по вложению бикластеры довольно давно и хорошо исследованы с точки зрения алгебраической структуры в рамках ФАП. Это подтверждает следующее утверждение.
Определение максимального по вложению бикластера 2.19 и определение формального понятия 2.12 эквивалентны.
Благодаря утверждению 2.1, для бикластеров, предложенных в этой вычислительной модели, можно построить иерархию по отношению покрытия, графически представляющую собой диаграмму решетки формальных понятий.
2.2.2. Описание алгоритма
Алгоритм BiMax следует стратегии "разделяй и властвуй". Первоначально алгоритм определяет области матрицы 
,
содержащие только 0, и затем исключает их из дальнейшего рассмотрения. Эта стратегия особенно выигрышна при условии разреженных данных, получение которых из исходных наборов зависит от выбора порога отсечения. В экспериментах, представленных в статье [13], для всех наборов данных доля 1-значений не превышает 6%.
Идея, лежащая в основе алгоритма, состоит в следующем: исходная матрица
разбивается на три подматрицы, одна из которых содержит только нулевые значения и в дальнейшем не рассматривается. Затем алгоритм рекурсивно применяется к оставшимся двум подматрицам 
и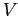 
.
Рекурсия прекращается, если текущая матрица, представляющая собой бикластер, содержит только единицы.
Для обработки подматрицы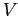
необходимы специальные операции, чтобы гарантировать максимальность по вложению бикластеров. Проблема возникает в том случае, если
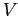содержит части бикластеров, найденных в ;
поэтому необходимо проводить проверку того, что алгоритм рассматривает только те бикластеры, которые расширяются в 
.
С этой целью вводится параметр 
,
который содержит множества столбцов, ограничивающие число допустимых бикластеров. Бикластер
допустим, если
обладает одним или несколькими столбцами с каждым множеством столбцов 
из
, т.е.
.
2.3. Шумоустойчивые понятия
В связи с тем, что в исходных 0/1 данных, имеющих объектно-признаковую природу, могут присутствовать ошибочные значения (пропущенные объекты/признаки или напротив лишние) использование Формального Анализа Понятий приводит к увеличению количества формальных понятий. Чтобы избежать порождения таких нерелевантных понятий, необходимы новые типы структур, учитывающие шум такого рода. В качестве одной из таких структур в работе [19] предложено понятие плотного и релевантного бимножеств (DR-bi-set). Одно из свойств DR-бимножества, называющееся плотностью, состоит в том, что внутри подматрицы, образующей такое бимножество, допускается некоторое количество нулей. Формальное понятие является частным случаем DR-бимножества, для которого число нулевых элементов внутри подматрицы равно 0. Ниже будут рассмотрены основные определения и свойства DR-бимножеств, а также приведено описание алгоритма DR-miner.
2.3.1. Описание модели DR-бимножеств
Бимножеством будем называть пару 
,
принадлежащую декартовому произведению
.
Частным случаем бимножеств являются формальные понятия. Приведем определения, которые помогут провести обобщение формальных понятий до бимножеств.
число нулевых значений объекта 
на признаках из 
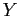
, т.е.
. Сходным образом через
определим число нулевых значений признака y на объектах из 
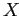
.Теперь формальные понятия можно ввести с помощью леммы.
 или, аналогично  |
(2.1) |
 и  |
(2.2) |
Отношение "быть более частным" (отношение "специализации") в модели вводится иначе, чем это принято для решеток понятий. А именно, требование антимонотонности для содержания понятия заменяется требованием монотонности.
тогда и только тогда, когда
и
.
Ограничение 
называется антимонотонным в смысле отношения 
тогда и только тогда, когда
таких, что
.
Двойственным образом,
называется монотонным в смысле отношения
тогда и только тогда, когда
.
Заметим, что 
означает, что бимножество 
удовлетворяет ограничению .
Ограничение на минимальный размер компонент бимножества выглядит следующим образом
. Такое ограничение монотонно по отношению
.
С помощью монотонного ограничения на допустимое число нулей, приходящихся на признак или объект, можно контролировать число нулей внутри бимножества, сохраняя при этом строгую связь между компонентами бимножества.
и положительное целое число 
, тогда
называется плотными тогда и только тогда, когда оно удовлетворяет антимонотонному ограничению
и
Необходимо извлекать такие бимножества
, для которых объекты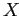
(соответственно, признаки )
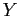имеют большую плотность единичных значений на признаках из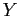
(соответственно на объектах из ),
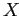чем на других признаках, т.е. на
(соответственно, на объектах
).
Такое требование приводит к ограничению релевантности, в котором параметр 
выражает разность нулевых значений внутри и вне бимножеств.
и положительное целое число ,
тогда
называется релевантным тогда и только тогда, когда оно удовлетворяет следующему ограничению:
и
Фактически, плотные и релевантные бимножества являются обобщением формальных понятий, которые можно рассматривать как бимножества при значениях 
и 
.
— обобщение первого уравнения леммы 2.1 , 
обобщает второе уравнение этой леммы, означающее, что все внешние элементы по отношению к данному бимножеству содержат по крайней мере
нулевых значений в дополнение к уже имеющимся для каждого внутреннего элемента. Параметр
отвечает за плотность внутри бимножества, а параметр
показывает значимость разности с внешними элементами. Свойство
антимонотонно по отношению
и может быть использовано для эффективного отсечения. Свойство
не является ни монотонным, ни антимонотонным, но его также можно эффективно использовать.
(т.е. удовлетворяющее
).
называется DR-бимножеством тогда и только тогда, когда оно максимально по отношению ,
т.е. не существует
такого, что 
удовлетворяет
и
.
Множество всех таких пар контекста 
при заданных
и
обозначается как
. Отметим, что для объектов и признаков можно ввести различные пороги
и
.