Методы бикластеризации для анализа интернет-данных

Дмитрий Игнатов,
кафедра анализа данных и искусственного интеллекта ГУ-ВШЭ

Назад Содержание Вперёд

1.2. Типы данных

Как уже говорилось выше, исходные данные представляют собой числовую матрицу. Значения этой матрицы в зависимости от необходимого представления данных могут принадлежать множеству действительных чисел или только лишь множеству . Значительная часть алгоритмов бикластеризации работает только с бинарными данными, например, BiMax, DR-miner и все алгоритмы поиска формальных понятий и частых (замкнутых) множеств признаков. И хотя существуют техники сведения вещественных и целочисленных данных к бинарным, такие как дискретизация и шкалирование, представляется необходимым четко разделять методы по типу данных.

1.3. Типы бикластеров

Укажем основные типы бикластеров, которые обнаруживают различные алгоритмы бикластеризации:

1. бикластер с постоянными значениями;
2. бикластер с постоянными значениями по строкам или столбцам;
3. бикластер с когерентными значениями;
4. бикластер с когерентными изменениями.

В таблице 1.1 приведены примеры основных типов бикластеров. Дадим пояснения:

1. бикластер с постоянными значениями,
2. бикластер с постоянными значениями по строкам,
3. бикластер с постоянными значениями по столбцам,
4. когерентные значения в рамках аддитивной модели,
5. когерентные значения в рамках мультипликативной модели,
6. когерентное изменение по всему бикластеру,
7. когерентное изменение по строкам,
8. когерентное изменение по столбцам,
9. когерентное возрастание и/или убывание значений генной экспрессии.

1.4. Структура бикластеров

Среди разработанных алгоритмов представлены как те, что находят только один бикластер, так и алгоритмы, порождающие множество бикластеров. Бикластеры, входящие в такое множество, могут иметь различную структуру. Приведем перечень возможных вариантов структуры бикластеров:

1. исключающие по строкам и столбцам бикластеры (прямоугольные диагональные блоки после переупорядочивания строк и столбцов);
2. неперекрывающиеся бикластеры со структурой шахматной доски;
3. бикластеры, исключающие пересечения по строкам;
4. бикластеры, исключающие пересечения по столбцам;
5. неперекрывающиеся бикластеры с древесной структурой;
6. неперекрывающиеся не исключающие пересечения бикластеры;
7. перекрывающиеся бикластеры с иерархической структурой;
8. произвольно расположенные перекрывающиеся бикластеры.

В таблице 1.2 проиллюстрированы различные типы структуры бикластеров. На рисунке буквой a обозначен одиночный бикластер,

2. исключающие пересечения по строкам и столбцам бикластеры,
3. неперекрывающиеся бикластеры со структурой шахматной доски,
4. бикластеры, исключающие пересечения по строкам,
5. бикластеры, исключающие пересечения по столбцам,
6. неперекрывающиеся бикластеры с древесной структурой,
7. неперекрывающиеся, не исключающие пересечения бикластеры,
8. перекрывающиеся бикластеры с иерархической структурой и
9. произвольно расположенные перекрывающиеся бикластеры.

1.5. Алгоритмические стратегии поиска

Алгоритмы бикластеризации могут порождать либо один бикластер, либо несколько, в зависимости от типа задачи. Например, алгоритм Ченга и Черча [25] находит один бикластер за проход, а для нахождения следующих необходимо маскировать найденный случайными числами и выполнить повторный запуск алгоритма. Другие бикластерные подходы позволяют находить множество бикластеров за проход. Существуют также алгоритмы, которые позволяют осуществлять одновременное выявление бикластеров.

Принимая во внимание вычислительную сложность проблемы, было предложено большое число эвристик. Эти стратегии поиска можно разделить на пять классов:

1. итеративная комбинация кластеризации по строкам и столбцам;
2. стратегия разделяй и властвуй;
3. жадная стратегия итеративного поиска;
4. полное перечисление бикластеров;
5. определение параметров распределения.

1.6. Классификация методов бикластеризации

Теперь, когда четко выделены основания для классификации алгоритмов бикластеризации, построим их таксономию. В таблице 1.3 для каждого алгоритма, вошедшего в обзор, в соответствующих столбцах указаны тип бикластера, структура порождаемых бимножеств, количество бикластеров, порожденных за один запуск алгоритма, и стратегия поиска.

Таблица 1.3: Сравнительная таблица алгоритмов бикластеризации

Алгоритм	Тип бикластера	Структура	Порождение	Стратегия поиска
Block Clustering [37]	Constant	f	One Set at a Time	Div-and-Conq
-biclusters [25]	Coherent Values	i	One at a Time	Greedy
FLOC [84,85]	Coherent Values	i	Simultaneous	Greedy
pClusters [81]	Coherent Values	g	Simultaneous	Exh-Enum
Plaid Models [51]	Coherent Values	i	One at a Time	Dist-Ident
PRMs [66,67]	Coherent Values	i	Simultaneous	Dist-Ident
CTWC [34]	Constant Columns	i	One Set at a Time	Clust-Comb
ITWC [78]	Coherent Values	d,e	One Set at a Time	Clust-Comb
DCC [23]	Constant	b,c	Simultaneous	Clust-Comb
-Patterns [24]	Constant Rows	i	Simultaneous	Greedy
Spectral [45]	Coherent Values	c	Simultaneous	Greedy
Gibbs [68]	Constant Columns	d,e	One at a Time	Dist-Ident
OPSMs [16]	Coherent Evolution	a,i	One at a Time	Greedy
SAMBA [77]	Coherent Evolution	i	Simultaneous	Exh-Enum
xMOTIFs [58] [19]	Coherent Evolution	a,i	Simultaneous	Greedy
OP-Clusters [53]	Coherent Evolution	i	Simultaneous	Exh-Enum

Мы используем решеточную таксономию алгоритмов, так как она лишена недостатков древесной, когда наследование свойств от различных надклассов невозможно для одного и того же подкласса. Данная таксономия построена средствами ФАП, а исходная таблица 1.3 посредством шкалирования сведена к объектно-признаковому представлению в виде бинарной матрицы.

Мы предлагаем расширить указанную таксономию за счет введения дополнительного признака — типа исходных значений. Помимо этого, представляется желательным учесть тип бикластеров, в котором возможно присутствие некоторого числа нулевых значений, т.к. это один из способов ослабления требования к формальным понятиям. Для случая иерархической структуры бикластеров можно выделить и отдельно рассмотреть частичный (решеточный) порядок в качестве подтипа.

Для пополнения таксономии объектами мы предлагаем включить алгоритмы, используемые в ФАП для поиска формальных понятий, алгоритмы поиска частых (замкнутых) множеств признаков, алгоритм аддитивной бокс-кластеризации, DR-miner и D-miner из области DataMining, BiMax — разработанный для анализа генетических данных. Перечисленные алгоритмы, за исключением бокс-кластеризации, работают только с 0/1 данными, поэтому в таксономии им соответствует подрешетка, порожденная признаком
" -данные".

2. Модели и методы бикластеризации

2.1. Теория решёток и Формальный Анализ Понятий

Формальный Анализ Понятий — область прикладной математики, объектами исследования в которой являются (формальные) понятия и их иерархии. Прилагательное "формальный" указывает на наличие строгого математического определения понятия, как пары множеств, называемых, следуя традициям принятым в философии, объемом и содержанием. Формализация этих определений стала возможной благодаря использованию аппарата алгебраической теории решеток. Включение подраздела, посвященного ФАП, в раздел о методах и моделях бикластеризации обосновано широким спектром задач из области анализа данных, в которых ключевым является поиск бикластеров особого рода — формальных понятий. Мы не будем описывать алгоритмы ФАП в данной работе, поскольку им посвящены целые обзоры [47], а дадим лишь основные определения, составляющие основу вычислительной модели наших экспериментов.

2.1.1. Частично упорядоченные множества и решётки

Определение 2.1   Бинарное отношение на некотором множестве называется отношением (нестрогого) частичного порядка, если для :

1. (рефлексивность);
2. и , то (антисимметричность);
3. и , то (транзитивность).

Множество S с определённым на нем отношением частичного порядка (частично упорядоченное множество) обозначается . Если , то говорят, что элемент меньше, чем , или равен ему. Если для не существует , такого что , то называют максимальным элементом (относительно ).

Если и , то пишут и говорят, что строго меньше, чем .

Определение 2.2   Пусть — частично упорядоченное множество. Элемент называется соседом снизу элемента , если и . В этом случае называется соседом сверху 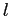(обозначается ). Направленный граф отношения называется графом покрытия.

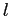Конечное частично упорядоченное множество может быть графически представлено с помощью диаграммы Хассе (или просто диаграммы [1]). Элементы изображаются в виде точек. Если , то размещается "над" (вертикальная координата больше вертикальной координаты 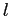), и две точки соединяются линией.

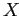
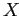
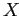
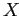
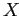
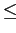
Определение 2.3   Верхней гранью подмножества в упорядоченном множестве называется элемент , такой что для всех . Точная верхняя грань множества (называемая также наименьшей верхней гранью или супремумом) множества (обозначается sup ) есть верхняя грань такая, что для любой верхней грани подмножества . Двойственным образом (с заменой на ) определяется понятие точной (наибольшей) нижней грани или инфимума inf .

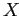
Определение 2.4   Бинарная операция называется полурешёточной, если для некоторого и любых :

1. (идемпотентность);
2. (коммутативность);
3. (ассоциативность);
4. .

Для и мы пишем вместо . Если , то .

Определение 2.5   Множество с определённой на нем полурешёточной операцией называется полурешёткой .

Определение 2.6   Пусть — полурешётка. Множество называется системой замыканий [33] или семейством Мура [1] (относительно ), если .

Очевидно, что система замыканий (относительно ) с определённой на ней операцией, и , образует полурешётку.

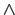
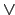
Определение 2.7   Упорядоченное множество с определёнными на нем полурешёточными операциями и называется решёткой, если и являются, соответственно, нижней и верхней полурешётками (относительно ).

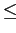
Операци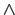и и 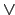называют операциями взятия точной нижней и верхней грани в решётке, или инфимума и супремума соответственно.

Определение 2.8   Подрешёткой решётки называется подмножество такое, что если , , то и .

Полурешёточные операци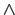и и 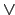удовлетворяют в решётках следующему условию: (поглощение).

Из любой конечной полурешётки можно получить решётку добавлением одного (максимального или минимального в зависимости от типа полурешетки) элемента.

Решётка называется полной, если у каждого подмножества его элементов есть супремум и инфимум (всякая конечная решётка является полной).

Определение 2.9   Интервал состоит из всех элементов , которые удовлетворяют неравенствам . Порядковым фильтром (идеалом) решётки называется подмножество такое, что если , и , то (соответственно, , и , то ).

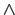Элемент решётки называется инфимум-неразложимым или -неразложимым (или неразложимым в пересечение), если для любых и , не выполняется . Элемент решётки называется супремум-неразложимым или 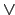-неразложимым (или неразложимым в объединение), если для любых и не выполняется .

Подмножество полной решётки называется инфимум-плотным, если , и супремум-плотным, если ).

Определение 2.10   Пусть и — частично упорядоченные множества. Пара отображений и называется соответствием Галуа между частично упорядоченными множествами и , если для любых и :

1. ;
2. ;
3. и .

Приведённые условия эквивалентны одному:  [1,33,28].

Назад Содержание Вперёд