Next: А. Конан Дойл, ``Пляшущие человечки'' Up: 7. Олимпиады по криптографии Previous: 7.1. Введение Contents: Содержание

7.2. Шифры замены

Наиболее известными и часто используемыми шифрами являются шифры замены. Они характеризуются тем, что отдельные части сообщения (буквы, слова, ...) заменяются на какие-либо другие буквы, числа, символы и т.д. При этом замена осуществляется так, чтобы потом по шифрованному сообщению можно было однозначно восстановить передаваемое сообщение.

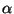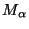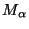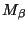Пусть, например, зашифровывается сообщение на русском языке и при этом замене подлежит каждая буква сообщения. Формально в этом случае шифр замены можно описать следующим образом. Для каждой буквы исходного алфавита строится некоторое множество символов  так, что множества и попарно не пересекаются при 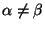, то есть любые два различные множества не содержат одинаковых элементов. Множество 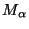называется множеством шифробозначений для буквы .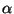

Таблица

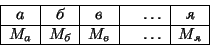(1)

является ключом шифра замены. Зная ее, можно осуществить как зашифрование, так и расшифрование.

При зашифровании каждая бук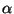ва открытого сообщения, начиная с первой, заменяется любым символом из множества 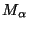. Если в сообщении содержится несколько букв 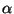, то каждая из них заменяется на любой символ из 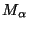. За счет этого с помощью одного ключа (1) можно получить различные варианты зашифрованного сообщения для одного и того же открытого сообщения. Например, если ключом является таблица

а б в г д е ж з и к л м н о п р 21 37 14 22 01 24 62 73 46 23 12 08 27 53 35 04 40 26 63 47 31 83 88 30 02 91 72 32 77 68 60 44 10 03 71 82 15 70 11 55 90 69 38 61 54 09 84 45 с т у ф х ц ч ш щ ъ ы ь э ю я 20 13 59 25 75 43 19 29 06 65 74 48 36 28 16 52 39 07 49 33 85 58 80 50 34 17 56 78 64 41 89 67 93 76 18 51 87 66 81 92 42 79 86 05 57

то сообщение ``я знаком с шифрами замены'' может быть зашифровано, например, любым из следующих трех способов:

16 55 54 10 69 09 61 89 29 90 49 44 10 08 02 73 21 32 83 54 74 41 55 77 10 23 68 08 20 66 90 76 44 21 61 90 55 21 61 83 54 42 57 30 27 10 91 68 32 20 80 02 49 45 40 32 46 55 40 08 83 27 42

Так как множества 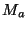, , 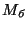, 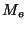..., 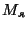попарно не пересекаются, то по каждому символу шифрованного сообщения можно однозначно определить, какому множеству он принадлежит, и, следовательно, какую букву открытого сообщения он заменяет. Поэтому расшифрование возможно и открытое сообщение определяется единственным образом.

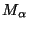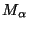Часто состоит из одного элемента. Например, в романе Ж. Верна ``Путешествие к центру Земли'' в руки профессора Лиденброка попадает пергамент с рукописью из знаков рунического письма. Каждое множество состоит из одного элемента. Элемент каждого множества выбирается из набора символов вида

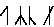(2)

В рассказе А. Конан Дойла ``Пляшущие человечки'' каждый символ изображает пляшущего человечка в самых различных позах

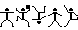(3)

На первый взгляд кажется, что чем хитрее символы, тем труднее вскрыть сообщение, не имея ключа. Это, конечно, не так. Если каждому символу однозначно сопоставить какую-либо букву или число, то легко перейти к зашифрованному сообщению из букв или чисел. В романе Ж. Верна ``Путешествие к центру Земли'' каждый рунический знак был заменен на соответствующую букву немецкого языка, что облегчило восстановление открытого сообщения. С точки зрения криптографов использование различных сложных символов не усложняет шифра. Однако, если зашифрованное сообщение состоит из букв или цифр, то вскрывать такое сообщение удобнее.

Рассмотрим некоторые примеры шифров замены. Пусть каждое множество 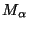состоит из одной буквы. Например,

(4)

Такой шифр называется шифром простой однобуквенной замены. По ключу (4) удобно проводить зашифрование и расшифрование: при зашифровании каждая буква открытого текста заменяется на соответствующую букву из второй строки (а на г и т.д.) При расшифровании, наоборот, г заменяется на а и т.д. При шифровании и расшифровании надо помнить вторую строчку в (4), то есть ключ.

Запомнить произвольный порядок букв алфавита достаточно сложно. Поэтому всегда пытались придумать какое-либо правило, по которому можно просто восстановить вторую строчку в (4).

Одним из первых шифров, известных из истории, был так называемый шифр Цезаря, для которого вторая строка в (4) является последовательностью, записанной в алфавитном порядке, но начинающейся не с буквы а:

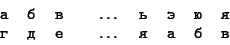(5)

В одной из задач (задача 4.4) используется шифр Цезаря. Запомнить ключ в этом случае просто - надо знать первую букву второй строки (4) (последовательность букв в алфавите предполагается известной). Однако такой шифр обладает большим недостатком. Число различных ключей равно числу букв в алфавите. Перебрав эти варианты, можно однозначно восстановить открытое сообщение, так как при правильном выборе ключа получится ``осмысленный'' текст. В других случаях обычно получается ``нечитаемый'' текст. Задача 4.4 именно на это и рассчитана. Несмотря на то, что используется фраза на латинском языке, которого школьники не знают, многие участники олимпиады смогли указать открытое сообщение.

Другим примером шифра замены может служить лозунговый шифр. Здесь запоминание ключевой последовательности основано на лозунге - легко запоминаемом слове. Например, выберем слово-лозунг ``учебник'' и заполним вторую строку таблицы по следующему правилу: сначала выписываем слово-лозунг, а затем выписываем в алфавитном порядке буквы алфавита, не вошедшие в слово-лозунг. Вторая строка в (4) примет вид

у ч е б н и к а в г д ж з л м о

п р с т ф х ц ш щ ъ ы ь э ю я

В данном случае число вариантов ключа существенно больше числа букв алфавита.

Рассмотренные шифры имеют одну слабость. Если в открытом сообщении часто встречается какая-либо буква, то в шифрованном сообщении часто будет встречаться соответствующий ей символ или буква. Поэтому при вскрытии шифра замены обычно стараются наиболее часто встречающимся символам шифрованного сообщения поставить в соответствие буквы открытого сообщения с наибольшей предполагаемой частотой появления. Если шифрованное сообщение достаточно большое, то этот путь приводит к успеху, даже если вы не знаете ключа.

Кроме частоты появления букв, могут быть использованы другие обстоятельства, помогающие раскрыть сообщение. Например, может быть известна разбивка на слова, как в задаче 4.2, и расставлены знаки препинания. Рассматривая небольшое число возможных вариантов замены для предлогов и союзов, можно попытаться определить часть ключа. В этой задаче существенно используется, какие гласные или согласные могут быть удвоенными: ``нн'', ``ее'', ``ии'' и др.

При анализе шифрованного сообщения следует исходить из того, что число различных вариантов для части определяемого ключа не такое уж большое, если вы находитесь на правильном пути. В противном случае либо вы получите противоречие, либо число вариантов ключа будет сильно возрастать. Обычно, начиная с некоторого момента определение открытого сообщения становится делом техники. Так, в задаче 4.2, если вы определили ``денно и нощно'', то дальнейшее определение открытого текста не представляет труда.

Вообще-то можно сказать, что вскрытие шифров замены является искусством и достаточно трудно формализовать этот процесс.

Популярные у школьников криптограммы (типа рассмотренной в задаче 1.5) по сути дела являются шифром замены с ключом

0 1 2 3 4 5 6 7 8 9 ш и ф р з а м е н ы

в котором каждой цифре ставится в соответствие буква. При этом должны соблюдаться правила арифметики. Эти правила значительно облегчают определение открытого текста, так же, как правила синтаксиса и орфографии в задаче 4.2 облегчают нахождение четверостишия В. Высоцкого.

Любые особенности текста, которые могут быть вам известны, - ваши помощники. Например, в задаче 5.2 прямо сказано, что в тексте есть выражения ``зпт'', ``тчк'', как часто бывает в реальных телеграммах. И эта подсказка - путь к решению задачи.

Шифрование даже относительно небольших текстов на одном ключе для рассмотренных шифров замены создает условия для вскрытия открытых сообщений. Поэтому такие шифры пытались усовершенствовать. Одно из направлений - построение шифров разнозначной замены, когда каждой букве ставится в соответствие один или два символа. (Простейшим примером является шифр, определяемый в задаче 4.2.) Например,

а б в г д е ж з и к л м н о п р 73 74 51 65 2 68 59 1 60 52 75 61 8 66 58 3 с т у ф х ц ч ш щ ъ ы ь э ю я 69 64 53 54 9 62 71 4 67 56 72 63 55 70 57

Если шифрованное сообщение написано без пробелов между символами, то появляется дополнительная трудность при разбиении шифрованного сообщения на отдельные символы и слова.

Другое направление создания шифров замены состоит в том, чтобы множества шифробозначений 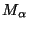 содержали более одного элемента. Такие шифры получили название шифров многозначной замены. Они позволяют скрыть истинную частоту букв открытого сообщения, что существенно затрудняет вскрытие этих шифров. Главная трудность, которая возникает при использовании таких шифров, заключается в запоминании ключа. Надо запомнить не одну строчку, а для каждой буквы алфавита 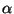 - множество ее шифробозначений 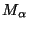. 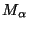Как правило, элементами множеств являются числа. Из художественной литературы и кинофильмов про разведчиков вам известно, что во время второй мировой войны часто использовались так называемые книжные шифры. Множество шифробозначений для каждой буквы определяется всеми пятизначными наборами цифр, в каждом из которых первые две цифры указывают номер страницы, третья цифра - номер строки, четвертая и пятая цифры - номер места данной буквы в указанной строке. Поэтому при поимке разведчика всегда пытались найти книгу, которая могла быть использована им в качестве ключа.

Мы не останавливаемся здесь на более сложных методах построения шифров замены. Приведенных примеров достаточно, чтобы оценить многообразие таких шифров. Но все они имеют серьезный недостаток - на одном ключе нельзя шифровать достаточно длинные сообщения. Поэтому, как правило, шифры замены используются в комбинации с другими шифрами. Чаще всего - с шифрами перестановки, о которых вы прочитаете в следующем разделе.

В заключение, следуя героям известных литературных произведений, вскроем некоторые шифры замены. Обратите внимание на то, какие неожиданные обстоятельства при этом используются. Действительно, вскрытие шифров - искусство.

Next: А. Конан Дойл, ``Пляшущие человечки'' Up: 7. Олимпиады по криптографии Previous: 7.1. Введение Contents: Содержание