2004 г
Назад Оглавление Вперёд
9. Генерация
кода
Задача
генератора
кода -
построение
для
программы
на входном
языке
эквивалентной
машинной
программы.
Обычно в
качестве
входа для
генератора
кода служит
некоторое
промежуточное
представление
программы.
Генерация
кода
включает
ряд
специфических,
относительно
независимых
подзадач:
распределение
памяти (в
частности,
распределение
регистров),
выбор
команд,
генерацию
объектного
(или
загрузочного)
модуля.
Конечно,
независимость
этих
подзадач
относительна:
например,
при выборе
команд
нельзя не
учитывать
схему
распределения
памяти, и,
наоборот,
схема
распределения
памяти
(регистров,
в частности)
ведет к
генерации
той или иной
последовательности
команд.
Однако
удобно и
практично
эти задачи
все же
разделять,
обращая
при этом
внимание
на их
взаимодействие.
В какой-то
мере схема
генератора
кода
зависит
от формы
промежуточного
представления.
Ясно, что
генерация
кода из
дерева
отличается
от генерации
кода из
троек, а
генерация
кода из
префиксной
записи
отличается
от генерации
кода из
ориентированного
графа.
В то же
время все
генераторы
кода имеют
много
общего, и
основные
применяемые
алгоритмы
отличаются,
как правило,
только в
деталях,
связанных с
используемым
промежуточным
представлением.
В дальнейшем
в качестве
промежуточного
представления
мы будем
использовать
префиксную
нотацию.
А именно,
алгоритмы
генерации
кода будем
излагать
в виде
атрибутных
схем со
входным
языком
Лидер.
9.1 Модель
машины
При
изложении
алгоритмов
генерации
кода мы
будем
следовать
некоторой
модели
машины,
в основу
которой
положена
система
команд
микропроцессора
Motorola MC68020. В
микропроцессоре
имеется
регистр -
счетчик
команд PC, 8
регистров
данных и 8
адресных
регистров.
В системе
команд
используются
следующие
способы
адресации:
ABS - абсолютная:
исполнительным
адресом
является
значение
адресного
выражения.
IMM - непосредственный
операнд:
операндом
команды
является
константа,
заданная в
адресном
выражении.
D - прямая
адресация
через
регистр
данных,
записывается
как Хn,
операнд
находится
в регистре
Хn.
А - прямая
адресация
через
адресный
регистр,
записывается
как An, операнд
находится
в регистре
An.
INDIRECT - записывается
как (An), адрес
операнда
находится
в адресном
регистре
An.
POST - пост-инкрементная
адресация,
записывается
как (Аn)+,
исполнительный
адрес есть
значение
адресного
регистра
An и после
исполнения
команды
значение
этого
регистра
увеличивается
на длину
операнда.
PRE - пре-инкрементная
адресация,
записывается
как -(Аn): перед
исполнением
операции
содержимое
адресного
регистра An
уменьшается
на длину
операнда,
исполнительный
адрес
равен
новому
содержимому
адресного
регистра.
INDISP - косвенная
адресация
со смещением,
записывается
как (bd,An),
исполнительный
адрес
вычисляется
как (An)+d -
содержимое
An плюс d.
INDEX - косвенная
адресация
с индексом,
записывается
как (bd,An,Xn*sc),
исполнительный
адрес
вычисляется
как (An)+bd+(Xn)*sc -
содержимое
адресного
регистра +
адресное
смещение +
содержимое
индексного
регистра,
умноженное
на sc.
INDIRPC - косвенная
через PC
(счетчик
команд),
записывается
как (bd,PC),
исполнительный
адрес
определяется
выражением
(PC)+bd.
INDEXPC - косвенная
через PC со
смещением,
записывается
как (bd,PC,Xn*sc),
исполнительный
адрес
определяется
выражением
(PC)+bd+(Xn)*sc.
INDPRE - пре-косвенная
через
память,
записывается
как ([bd,An,sc*Xn],od)
(схема
вычисления
адресов
для этого
и трех
последующих
способов
адресации
приведена
ниже).
INDPOST - пост-косвенная
через
память: ([bd,An],sc*Xn,od).
INDPREPC - пре-косвенная
через PC: ([bd,PC,sc*Xn],od).
INDPOSTPC - пост-косвенная
через PC: ([bd,PC],Xn,od).
Здесь bd -
это 16- или
32-битная
константа,
называемая
смещением,
od - 16- или
32-битная
литеральная
константа,
называемая
внешним
смещением.
Эти способы
адресации
могут
использоваться
в упрощенных
формах без
смещений bd
и/или od и без
регистров
An или Xn.
Следующие
примеры
иллюстрируют
косвенную
постиндексную
адресацию:
MOVE D0, ([A0])
MOVE D0, ([4,A0])
MOVE D0, ([A0],6)
MOVE D0, ([A0],D3)
MOVE D0, ([A0],D4,12)
MOVE D0, ([$12345678,A0],D4,$FF000000)
|
Индексный
регистр
Xn может
масштабироваться
(умножаться)
на 2,4,8, что
записывается
как sc*Xn.
Например, в
исполнительном
адресе ([24,A0,4*D0])
содержимое
квадратных
скобок
вычисляется
как [A0] + 4 * [D0] + 24.
Эти способы
адресации
работают
следующим
образом.
Каждый
исполнительный
адрес
содержит
пару
квадратных
скобок [...]
внутри пары
круглых
скобок, т.е.
([...], ... ). Сначала
вычисляется
содержимое
квадратных
скобок, в
результате
чего
получается
32-битный
указатель.
Например,
если
используется
постиндексная
форма [20,A2], то
исполнительный
адрес
- это 20 + [A2].
Аналогично,
для
преиндексной
формы [12,A4,D5]
исполнительный
адрес -
это 12 + [A4] + [D5].
Указатель,
сформированный
содержимым
квадратных
скобок,
используется
для доступа
в память,
чтобы
получить
новый
указатель
(отсюда
термин
косвенная
адресация
через
память).
К этому
новому
указателю
добавляется
содержимое
внешних
круглых
скобок
и таким
образом
формируется
исполнительный
адрес
операнда.
В дальнейшем
изложении
будут
использованы
следующие
команды (в
частности,
рассматриваются
только
арифметические
команды
с целыми
операндами,
но не с
плавающими):
MOVEA ИА, А -
загрузить
содержимое
по исполнительному
адресу ИА
на адресный
регистр
А.
MOVE ИА1, ИА2 -
содержимое
по исполнительному
адресу ИА1
переписать
по исполнительному
адресу ИА2.
MOVEM список_регистров, ИА
- сохранить
указанные
регистры
в памяти,
начиная с
адреса ИА
(регистры
указываются
маской
в самой
команде).
MOVEM ИА, список_регистров
- восстановить
указанные
регистры
из памяти,
начиная с
адреса ИА
(регистры
указываются
маской
в самой
команде).
LEA ИА, А -
загрузить
исполнительный
адрес ИА на
адресный
регистр
А.
MUL ИА, D -
умножить
содержимое
по исполнительному
адресу ИА на
содержимое
регистра
данных D и
результат
разместить
в D (на самом
деле в
системе
команд
имеются две
различные
команды MULS и
MULU для чисел
со знаком
и чисел
без знака
соответственно;
для
упрощения
мы не будем
принимать
во внимание
это
различие).
DIV ИА, D -
разделить
содержимое
регистра
данных D на
содержимое
по исполнительному
адресу ИА и
результат
разместить
в D.
ADD ИА, D -
сложить
содержимое
по исполнительному
адресу ИА с
содержимым
регистра
данных D и
результат
разместить
в D.
SUB ИА, D -
вычесть
содержимое
по исполнительному
адресу ИА из
содержимого
регистра
данных D и
результат
разместить
в D.
Команды CMP и TST
формируют
разряды
регистра
состояний.
Всего
имеется 4
разряда: Z
- признак
нулевого
результата,
N - признак
отрицательного
результата,
V - признак
переполнения,
C - признак
переноса.
CMP ИА, D - из
содержимого
регистра
данных D
вычитается
содержимое
по исполнительному
адресу ИА,
при этом
формируется
все разряды
регистра
состояний,
но содержимое
регистра D
не меняется.
TST ИА -
выработать
разряд Z
регистра
состояний
по значению,
находящемуся
по исполнительному
адресу ИА.
BNE ИА -
условный
переход по
признаку Z = 1
(не равно) по
исполнительному
адресу ИА.
BEQ ИА -
условный
переход по
признаку
Z = 0 (равно) по
исполнительному
адресу ИА.
BLE ИА -
условный
переход по
признаку N or Z
(меньше или
равно) по
исполнительному
адресу ИА.
BGT ИА -
условный
переход по
признаку not N
(больше) по
исполнительному
адресу ИА.
BLT ИА -
условный
переход по
признаку N
(меньше) по
исполнительному
адресу ИА.
BRA ИА -
безусловный
переход
по адресу
ИА.
JMP ИА -
безусловный
переход по
исполнительному
адресу.
RTD размер_локальных
- возврат из
подпрограммы
с указанием
размера
локальных.
LINK A, размер_локальных
- в стеке
сохраняется
значение
регистра А,
в регистр А
заносится
указатель
на это
место в
стеке и
указатель
стека
продвигается
на размер
локальных.
UNLK A - стек
сокращается
на размер
локальных
и регистр А
восстанавливается
из стека.
9.2 Динамическая
организация
памяти
Динамическая
организация
памяти - это
организация
памяти
периода
исполнения
программы.
Оперативная
память
программы
обычно
состоит из
нескольких
основных
разделов:
стек
(магазин),
куча,
область
статических
данных
(инициализированных
и неинициализированных).
Наиболее
сложной
является
работа со
стеком.
Вообще
говоря, стек
периода
исполнения
необходим
для
программ
не на всех
языках
программирования.
Например,
в ранних
версиях
Фортрана
нет
рекурсии,
так что
программа
может
исполняться
без стека.
С другой
стороны,
исполнение
программы
с рекурсией
может быть
реализовано
и без стека
(того же
эффекта
можно
достичь,
например,
и с помощью
списковых
структур).
Однако, для
эффективной
реализации
пользуются
стеком,
который,
как правило,
поддерживается
на уровне
машинных
команд.
Рассмотрим
схему
организации
магазина
периода
выполнения
для
простейшего
случая (как,
например,
в языке
Паскаль),
когда все
переменные
в магазине
(фактические
параметры
и локальные
переменные)
имеют
известные
при
трансляции
смещения.
Магазин
служит для
хранения
локальных
переменных
(и параметров)
и обращения
к ним в
языках,
допускающих
рекурсивные
вызовы
процедур.
Еще одной
задачей,
которую
необходимо
решать при
трансляции
языков с
блочной
структурой
- обеспечение
реализации
механизмов
статической
вложенности.
Пусть
имеется
следующий
фрагмент
программы
на Паскале:
procedure P1;
var V1;
procedure P2;
var V2;
begin
...
P2;
V1:=...
V2:=...
...
end;
begin
...
P2;
...
end;
|
В процессе
выполнения
этой
программы,
находясь в
процедуре
P2, мы должны
иметь
доступ к
последнему
экземпляру
значений
переменных
процедуры P2 и
к экземпляру
значений
переменных
процедуры P1,
из которой
была
вызвана P2.
Кроме того,
необходимо
обеспечить
восстановление
состояния
программы
при
завершении
выполнения
процедуры.
Мы рассмотрим
две
возможные
схемы
динамической
организации
памяти:
схему со
статической
цепочкой и
с дисплеем
в памяти.
В первом
случае все
статические
контексты
связаны
в список,
который
называется
статической
цепочкой;
в каждой
записи для
процедуры
в магазине
хранится
указатель
на запись
статически
охватывающей
процедуры
(помимо,
конечно,
указателя
динамической
цепочки -
указателя
на «базу»
динамически
предыдущей
процедуры).
Во втором
случае для
хранения
ссылок на
статические
контексты
используется
массив,
называемый
дисплеем.
Использование
той или
иной схемы
определяется,
помимо
прочих
условий,
прежде
всего
числом
адресных
регистров.
9.2.1 Организация
магазина со
статической
цепочкой
Итак, в
случае
статической
цепочки
магазин
организован,
как это
изображено
на рис. 9.1.
Таким
образом,
на запись
текущей
процедуры
в магазине
указывает
регистр BP (Base Pointer),
с которого
начинается
динамическая
цепочка. На
статическую
цепочку
указывает
регистр LP (Link Pointer).
В качестве
регистров BP и
LP в различных
системах
команд
могут
использоваться
универсальные,
адресные
или
специальные
регистры.
Локальные
переменные
отсчитываются
от регистра
BP вверх,
фактические
параметры
- вниз с
учетом
памяти,
занятой
точкой
возврата
и самим
сохраненным
регистром
BP.
Вызов
подпрограмм
различного
статического
уровня
производится
несколько
по-разному.
При вызове
подпрограммы
того же
статического
уровня, что и
вызывающая
подпрограмма
(например,
рекурсивный
вызов той
же самой
подпрограммы),
выполняются
следующие
команды:
Занесение фактических параметров в магазин
JSR A
|
Команда JSR A
продвигает
указатель SP,
заносит PC на
верхушку
магазина и
осуществляет
переход
по адресу
A. После
выполнения
этих команд
состояние
магазина
становится
таким,
как это
изображено
на рис. 9.2.
Занесение
BP, отведение
локальных,
сохранение
регистров
делает
вызываемая
подпрограмма
(см. ниже).
При вызове
локальной
подпрограммы
необходимо
установить
указатель
статического
уровня на
текущую
подпрограмму,
а при
выходе -
восстановить
его на
старое
значение
(охватывающей
текущую).
Для этого
исполняются
следующие
команды:
Занесение фактических параметров в магазин
MOVE BP, LP
SUB Delta, LP
JSR A
|
Здесь Delta -
размер
локальных
вызывающей
подпрограммы
плюс
двойная
длина
слова.
Магазин
после
этого
принимает
состояние,
изображенное
на рис. 9.3.
Предполагается,
что регистр
LP уже
сохранен
среди
сохраняемых
регистров,
причем
самым
первым
(сразу
после
локальных
переменных).
После
выхода из
подпрограммы
в вызывающей
подпрограмме
выполняется
команда
которая
восстанавливает
старое
значение
статической
цепочки.
Если выход
осуществлялся
из подпрограммы
1-го уровня,
эту команду
выполнять
не надо,
поскольку
для 1-го
уровня нет
статической
цепочки.
При вызове
подпрограммы
меньшего,
чем
вызывающая,
уровня
выполняются
следующие
команды:
Занесение фактических параметров в магазин
MOVE (LP), LP /* столько раз, какова разность
уровней вызывающей и вызываемой ПП */
JSR A
|
Тем самым
устанавливается
статический
уровень
вызываемой
подпрограммы.
После
выхода из
подпрограммы
выполняется
команда
восстанавливающая
статический
уровень
вызывающей
подпрограммы.
Тело
подпрограммы
начинается
со следующих
команд:
LINK BP , -размер_локальных
MOVEM -(SP)
|
Команда
LINK BP, размер_локальных
эквивалентна
трем
командам:
MOVE BP, -(SP)
MOVE SP, BP
ADD -размер_локальных, SP
|
Команда MOVEM
сохраняет
в магазине
регистры.
В результате
выполнения
этих команд
магазин
приобретает
вид,
изображенный
на рис. 9.1.
Выход из
подпрограммы
осуществляется
следующей
последовательностью
команд:
MOVEM (SP)+
UNLK BP
RTD размер_фактических
|
Команда MOVEM
восстанавливает
регистры из
магазина.
Команда UNLK BP
эквивалентна
такой
последовательности
команд:
MOVE BP,SP
MOVE (SP),BP
ADD #4, SP /* 4 - размер слова */
|
Команда
RTD размер_фактических,
в свою
очередь,
эквивалентна
последовательности
ADD размер_фактических+4, SP
JMP -размер_фактических-4(SP)
|
После ее
выполнения
магазин
восстанавливается
до состояния,
которое
было до
вызова.
В зависимости
от наличия
локальных
переменных,
фактических
параметров
и необходимости
сохранения
регистров
каждая
из этих
команд
может
отсутствовать.
9.2.2 Организация
магазина с
дисплеем
Рассмотрим
теперь
организацию
магазина с
дисплеем.
Дисплей -
это массив
(DISPLAY) , i-й элемент
которого
представляет
собой
указатель
на область
активации
последней
вызванной
подпрограммы
i-го статического
уровня.
Доступ к
переменным
самой
внутренней
подпрограммы
осуществляется
через
регистр BP.
Дисплей
может быть
реализован
либо через
регистры
(если их
достаточно),
либо через
массив в
памяти.
При вызове
процедуры
следующего
(по отношению
к вызывающей)
уровня в
дисплее
отводится
очередной
элемент.
Если
вызывающая
процедура
имеет
статический
уровень
i, то при
вызове
процедуры
уровня j  i
элементы
дисплея j, ..., i
должны быть
скопированы
(обычно
в стек
вызывающей
процедуры),
текущим
уровнем
становится
j и в DISPLAY[j]
заносится
указатель
на область
активации
вызываемой
процедуры.
По окончании
работы
вызываемой
процедуры
содержимое
дисплея
восстанавливается
из стека.
i
элементы
дисплея j, ..., i
должны быть
скопированы
(обычно
в стек
вызывающей
процедуры),
текущим
уровнем
становится
j и в DISPLAY[j]
заносится
указатель
на область
активации
вызываемой
процедуры.
По окончании
работы
вызываемой
процедуры
содержимое
дисплея
восстанавливается
из стека.
Иногда
используется
комбинированная
схема -
дисплей в
магазине.
Дисплей
хранится
в области
активации
каждой
процедуры.
Формирование
дисплея для
процедуры
осуществляется
в соответствии
с правилами,
описанными
выше.
Отдельного
рассмотрения
требует
вопрос о
технике
передачи
фактических
параметров.
Конечно,
в случае
простых
параметров
(например,
чисел)
проблем не
возникает.
Однако
передача
массивов по
значению -
операция
довольно
дорогая,
поэтому
с точки
зрения
экономии
памяти
целесообразнее
сначала в
подпрограмму
передать
адрес
массива,
а затем
уже из
подпрограммы
по адресу
передать
в магазин
сам массив.
В связи с
передачей
параметров
следует
упомянуть
еще одно
обстоятельство.
Рассмотренная
схема
организации
магазина
допустима
только для
языков со
статически
известными
размерами
фактических
параметров.
Однако,
например,
в языке
Модула-2 по
значению
может быть
передан
гибкий
массив,
и в этом
случае
нельзя
статически
распределить
память для
параметров.
Обычно
в таких
случаях
заводят так
называемый
«паспорт»
массива,
в котором
хранится
вся
необходимая
информация,
а сам массив
размещается
в магазине
в рабочей
области
выше
сохраненных
регистров.
9.3 Назначение
адресов
Назначение
адресов
переменным,
параметрам
и полям
записей
происходит
при
обработке
соответствующих
объявлений.
В однопроходном
трансляторе
это может
производиться
вместе с
построением
основной
таблицы
символов и
соответствующие
адреса (или
смещения)
могут
храниться
в этой же
таблице. В
промежуточном
представлении
Лидер
объявления
сохранены,
что
делает это
промежуточное
представление
машинно-независимым.
Напомним,
что в
Лидер-представлении
каждому
описанию
соответствует
некоторый
номер. В
процессе
работы
генератора
кодов
поддерживается
таблица Table,
в которой
по этому
номеру
(входу)
содержится
следующая
информация:
- для типа:
его размер;
- для
переменной:
смещение
в области
процедуры
(или
глобальной
области);
- для поля
записи:
смещение
внутри
записи;
- для
процедуры:
размер
локальных
параметров;
- для
массива:
размер
массива,
размер
элемента,
значение
левой и
правой
границы.
Функция IncTab
вырабатывает
указатель
(вход) на
новый
элемент
таблицы,
проверяя
при этом
наличие
свободной
памяти.
Для
вычисления
адресов
определим
для каждого
объявления
два
синтезируемых
атрибута:
DISP будет
обозначать
смещение
внутри
области
процедуры
(или единицы
компиляции),
а SIZE - размер.
Тогда
семантика
правила
для списка
объявлений
принимает
вид
RULE
DeclPart ::= ( Decl )
SEMANTICS
Disp<1>=0;
1A: Disp<1>=Disp<1>+Size<1>;
Size<0>=Disp<1>.
|
Все
объявления,
кроме
объявлений
переменных,
имеют
нулевой
размер.
Размер
объявления
переменной
определяется
следующим
правилом:
RULE
Decl ::= 'VAR' TypeDes
SEMANTICS
Tablentry Entry;
0: Entry=IncTab;
Size<0>=((Table[VAL<2>]+1) / 2)*2;
// Выравнивание на границу слова
Table[Entry]=Disp<0>+Size<0>.
|
В качестве
примера
трансляции
определения
типа
рассмотрим
обработку
описания
записи:
RULE
TypeDes ::= 'REC' ( TypeDes ) 'END'
SEMANTICS
int Disp;
Tablentry Temp;
0: Entry<0>=IncTab;
Disp=0;
2A: {Temp=IncTab;
Table[Temp]=Disp;
Disp=Disp+Table[Entry<2>]+1) / 2)*2;
// Выравнивание на границу слова
}
Table[Entry<0>]=Disp.
|
9.4 Трансляция
переменных
Переменные
отражают
все
многообразие
механизмов
доступа
в языке.
Переменная
имеет
синтезированный
атрибут ADDRESS -
это запись,
описывающая
адрес в
команде
МС68020. Этот
атрибут
сопоставляется
всем
нетерминалам,
представляющим
значения.
В системе
команд
МС68020 много
способов
адресации,
и они
отражены в
структуре
значения
атрибута ADDRESS,
имеющего
следующий
тип:
enum Register
{D0,D1,D2,D3,D4,D5,D6,D7,A0,A1,A2,A3,A4,A5,A6,SP,NO};
enum AddrMode
{D,A,Post,Pre,Indirect,IndPre,IndPost,IndirPC,
IndPrePC,IndPostPC,InDisp,Index,IndexPC,Abs,Imm};
struct AddrType{
Register AddrReg,IndexReg;
int IndexDisp,AddrDisp;
short Scale;
};
|
Значение
регистра NO
означает,
что
соответствующий
регистр в
адресации
не используется.
Доступ к
переменным
осуществляется
в зависимости
от их уровня:
глобальные
переменные
адресуются
с помощью
абсолютной
адресации;
переменные
в процедуре
текущего
уровня
адресуются
через
регистр
базы А6.
Если стек
организован
с помощью
статической
цепочки, то
переменные
предыдущего
статического
уровня
адресуются
через
регистр
статической
цепочки А5;
переменные
остальных
уровней
адресуются
«пробеганием»
по статической
цепочке с
использованием
вспомогательного
регистра.
Адрес
переменной
формируется
при
обработке
структуры
переменной
слева
направо и
передается
сначала
сверху
вниз как
наследуемый
атрибут
нетерминала
VarTail, а затем
передается
снизу-вверх
как
глобальный
атрибут
нетерминала
Variable. Таким
образом,
правило для
обращения к
переменной
имеет вид
(первое
вхождение
Number в правую
часть - это
уровень
переменной,
второе - ее
Лидер-номер):
RULE
Variable ::= VarMode Number Number VarTail
SEMANTICS
int Temp;
struct AddrType AddrTmp1, AddrTmp2;
3: if (Val<2>==0) // Глобальная переменная
{Address<4>.AddrMode=Abs;
Address<4>.AddrDisp=0;
}
else // Локальная переменная
{Address<4>.AddrMode=Index;
if (Val<2>==Level) // Переменная текущего уровня
Address<4>.AddrReg=A6;
else if (Val<2>==Level-1)
// Переменная предыдущего уровня
Address<4>.AddrReg=A5;
else
{Address<4>.Addreg=GetFree(RegSet);
AddrTmp1.AddrMode=Indirect;
AddrTmp1.AddrReg=A5;
Emit2(MOVEA,AddrTmp1,Address<4>.AddrReg);
AddrTmp1.AddrReg=Address<4>.AddrReg;
AddrTmp2.AddrMode=A;
AddrTmp2.AddrReg=Address<4>.AddrReg;
for (Temp=Level-Val<2>;Temp>=2;Temp-)
Emit2(MOVEA,AddrTmp1,AddrTmp2);
}
if (Val<2>==Level)
Address<4>.AddrDisp=Table[Val<3>];
else
Address<4>.AddrDisp=Table[Val<3>]+Table[LevelTab[Val<2>]];
}.
|
Функция GetFree
выбирает
очередной
свободный
регистр
(либо
регистр
данных, либо
адресный
регистр) и
отмечает
его как
использованный
в атрибуте RegSet
нетерминала
Block. Процедура Emit2
генерирует
двухадресную
команду.
Первый
параметр
этой
процедуры
- код
команды,
второй и
третий
параметры
имеют тип
AddrType и служат
операндами
команды.
Смещение
переменной
текущего
уровня
отсчитывается
от базы (А6),
а других
уровней - от
указателя
статической
цепочки,
поэтому оно
определяется
как
алгебраическая
сумма
размера
локальных
параметров
и величины
смещения
переменной.
Таблица
LevelTab - это
таблица
уровней
процедур,
содержащая
указатели
на последовательно
вложенные
процедуры.
Если стек
организован
с помощью
дисплея, то
трансляция
для
доступа к
переменным
может быть
осуществлена
следующим
образом:
RULE
Variable ::= VarMode Number Number VarTail
SEMANTICS
int Temp;
3: if (Val<2>==0) // Глобальная переменная
{Address<4>.AddrMode=Abs;
Address<4>.AddrDisp=0;
}
else // Локальная переменная
{Address<4>.AddrMode=Index;
if (Val<2>=Level) // Переменная текущего уровня
{Address<4>.AddrReg=A6;
Address<4>.AddrDisp=Table[Val<3>];
}
else
{Address<4>.AddrMode=IndPost;
Address<4>.AddrReg=NO;
Address<4>.IndexReg=NO;
Address<4>.AddrDisp=Display[Val<2>];
Address<4>.IndexDisp=Table[Val<3>];
}
}.
|
Рассмотрим
трансляцию
доступа
к полям
записи. Она
описывается
следующим
правилом
(Number - это
Лидер-номер
описания
поля):
RULE
VarTail ::= 'FIL' Number VarTail
SEMANTICS
if (Address<0>.AddrMode==Abs)
{Address<3>.AddrMode=Abs;
Address<3>.AddrDisp=Address<0>.AddrDisp+Table[Val<2>];
}
else
{Address<3>=Address<0>;
if (Address<0>.AddrMode==Index)
Address<3>.AddrDisp=Address<0>.AddrDisp+Table[Val<2>];
else
Address<3>.IndexDisp=Address<0>.IndexDisp+Table[Val<2>];
}.
|
9.5 Трансляция
целых
выражений
Трансляция
выражений
различных
типов
управляется
синтаксически
благодаря
наличию
указателя
типа перед
каждой
операцией.
Мы рассмотрим
некоторые
наиболее
характерные
проблемы
генерации
кода для
выражений.
Система
команд МС68020
обладает
двумя
особенностями,
сказывающимися
на генерации
кода для
арифметических
выражений
(то же можно
сказать и о
генерации
кода для
выражений
типа
«множества»):
1) один из
операндов
выражения
(правый)
должен при
выполнении
операции
находиться
на регистре,
поэтому
если оба
операнда
не на
регистрах,
то перед
выполнением
операции
один из
них надо
загрузить
на регистр;
2) система
команд
довольно
«симметрична»,
т.е. нет
специальных
требований
к регистрам
при
выполнении
операций
(таких,
например,
как пары
регистров
или
требования
четности
и т.д.).
Поэтому
выбор
команд при
генерации
арифметических
выражений
определяется
довольно
простыми
таблицами
решений.
Например,
для
целочисленного
сложения
такая
таблица
приведена
на рис. 9.4.
Здесь
имеется в
виду, что R -
операнд на
регистре, V -
переменная
или
константа.
Такая
таблица
решений
должна
также
учитывать
коммутативность
операций.
RULE
IntExpr ::= 'PLUS' IntExpr IntExpr
SEMANTICS
if (Address<2>.AddrMode!=D) && (Address<3>.AddrMode!=D)
{Address<0>.AddrMode=D;
Address<0>.Addreg=GetFree(RegSet);
Emit2(MOVE,Address<2>,Address<0>);
Emit2(ADD,Address<2>,Address<0>);
}
else
if (Address<2>.AddrMode==D)
{Emit2(ADD,Address<3>,Address<2>);
Address<0>:=Address<2>);
}
else {Emit2(ADD,Address<2>,Address<3>);
Address<0>:=Address<3>);
}.
|
9.6 Трансляция
арифметических
выражений
Одной из
важнейших
задач при
генерации
кода
является
распределение
регистров.
Рассмотрим
хорошо
известную
технику
распределения
регистров
при
трансляции
арифметических
выражений,
называемую
алгоритмом
Сети-Ульмана.
(Замечание:
в целях
большей
наглядности,
в данном
параграфе
мы немного
отступаем
от семантики
арифметических
команд MC68020 и
предполагаем,
что команда
Op Arg1, Arg2
выполняет
действие
Arg2:=Arg1 Op Arg2.)
Пусть
система
команд
машины
имеет
неограниченное
число
универсальных
регистров,
в которых
выполняются
арифметические
команды.
Рассмотрим,
как можно
сгенерировать
код,
используя
для данного
арифметического
выражения
минимальное
число
регистров.
Пусть
имеется
синтаксическое
дерево
выражения.
Предположим
сначала, что
распределение
регистров
осуществляется
по простейшей
схеме
сверху-вниз
слева-направо,
как
изображено
на рис. 9.5.
Тогда к
моменту
генерации
кода для
поддерева
LR занято n
регистров.
Пусть
поддерево
L требует nl
регистров, а
поддерево R -
nr регистров.
Если nl = nr,
то при
вычислении
L будет
использовано
nl регистров
и под
результат
будет
занят (n + 1)-й
регистр. Еще
nr(= nl) регистров
будет
использовано
при
вычислении
R. Таким
образом,
общее
число
использованных
регистров
будет
равно n + nl + 1.
Если nl > nr,
то при
вычислении
L будет
использовано
nl регистров.
При
вычислении
R будет
использовано
nr < nl регистров,
и всего
будет
использовано
не более чем
n+nl регистров.
Если nl < nr,
то после
вычисления
L под
результат
будет
занят один
регистр
(предположим,
(n + 1)-й) и nr
регистров
будет
использовано
для
вычисления
R. Всего
будет
использовано
n+nr+1 регистров.
Видно,
что для
деревьев,
совпадающих
с точностью
до порядка
потомков
каждой
вершины,
минимальное
число
регистров
при
распределении
их слева-направо
достигается
на дереве,
у которого
в каждой
вершине
слева
расположено
более
«сложное»
поддерево,
требующее
большего
числа
регистров.
Таким
образом,
если дерево
таково, что
в каждой
внутренней
вершине
правое
поддерево
требует
меньшего
числа
регистров,
чем левое,
то, обходя
дерево
слева
направо,
можно
оптимально
распределить
регистры.
Без
перестройки
дерева это
означает,
что если в
некоторой
вершине
дерева
справа
расположено
более
сложное
поддерево,
то сначала
сгенерируем
код для
него, а
затем уже
для левого
поддерева.
Алгоритм
работает
следующим
образом.
Сначала
осуществляется
разметка
синтаксического
дерева по
следующим
правилам.
Правила
разметки:
1) если
вершина
- правый
лист или
дерево
состоит из
единственной
вершины,
помечаем
эту вершину
числом
1, если
вершина -
левый лист,
помечаем
ее 0 (рис. 9.6).
2) если
вершина
имеет
прямых
потомков
с метками
l1 и l2, то в
качестве
метки этой
вершины
выбираем
наибольшее
из чисел l1
или l2 либо
число l1 + 1,
если l1 = l2 (рис. 9.7).
Эта
разметка
позволяет
определить,
какое из
поддеревьев
требует
большего
количества
регистров
для своего
вычисления.
Далее
осуществляется
распределение
регистров
для
результатов
операций по
следующим
правилам:
1) Корню
назначается
первый
регистр.
2) Если метка
левого
потомка
меньше
метки
правого,
то левому
потомку
назначается
регистр на
единицу
больший,
чем предку,
а правому
- с тем же
номером
(сначала
вычисляется
правое
поддерево
и его
результат
помещается
в регистр
R), так что
регистры
занимаются
последовательно.
Если же
метка
левого
потомка
больше
или равна
метке
правого
потомка, то
наоборот,
правому
потомку
назначается
регистр на
единицу
больший,
чем предку,
а левому
- с тем же
номером
(сначала
вычисляется
левое
поддерево
и его
результат
помещается
в регистр
R - рис. 9.7).
После
этого
формируется
код по
следующим
правилам:
1) если
вершина
- правый
лист с
меткой
1, то ей
соответствует
код
где R -
регистр,
назначенный
этой
вершине,
а X - адрес
переменной,
связанной
с вершиной
(рис. 9.8, б);
2) если
вершина
внутренняя
и ее левый
потомок
- лист с
меткой
0, то ей
соответствует
код
Код правого поддерева
Op X, R
|
где R -
регистр,
назначенный
этой
вершине,
X - адрес
переменной,
связанной с
вершиной, а Op
- операция,
примененная
в вершине
(рис. 9.8, а);
3) если
непосредственные
потомки
вершины
не листья
и метка
правой
вершины
больше
метки
левой, то
вершине
соответствует
код
Код правого поддерева
Код левого поддерева
Op R+1, R
|
где R -
регистр,
назначенный
внутренней
вершине, и
операция
Op, вообще
говоря, не
коммутативная
(рис. 9.9, б);
4) если
непосредственные
потомки
вершины
не листья
и метка
правой
вершины
меньше
или равна
метке
левой
вершины,
то вершине
соответствует
код
Код левого поддерева
Код правого поддерева
Op R, R+1
MOVE R+1, R
|
Последняя
команда
генерируется
для того,
чтобы
получить
результат
в нужном
регистре
(в случае
коммутативной
операции
операнды
операции
можно
поменять
местами и
избежать
дополнительной
пересылки
- рис. 9.9, а).
Рассмотрим
атрибутную
схему,
реализующую
эти правила
генерации
кода (для
большей
наглядности
входная
грамматика
соответствует
обычной
инфиксной
записи, а не
Лидер-представлению).
В этой
схеме
генерация
кода
происходит
не непосредственно
в процессе
обхода
дерева,
как раньше,
а из-за
необходимости
переставлять
поддеревья
код
строится
в виде
текста с
помощью
операции
конкатенации.
Практически,
конечно, это
нецелесообразно:
разумнее
управлять
обходом
дерева
непосредственно,
однако для
простоты
мы будем
пользоваться
конкатенацией.
RULE
Expr ::= IntExpr
SEMANTICS
Reg<1>=1; Code<0>=Code<1>; Left<1>=true.
RULE
IntExpr ::= IntExpr Op IntExpr
SEMANTICS
Left<1>=true; Left<3>=false;
Label<0>=(Label<1>==Label<3>)
? Label<1>+1
: Max(Label<1>,Label<3>);
Reg<1>=(Label<1> < Label<3>)
? Reg<0>+1
: Reg<0>;
Reg<3>=(Label<1> < Label<3>)
? Reg<0>
: Reg<0>+1;
Code<0>=(Label<1>==0)
? Code<3> + Code<2>
+ Code<1> + "," + Reg<0>
: (Label<1> < Label<3>)
? Code<3> + Code<1> + Code<2> +
(Reg<0>+1) + "," + Reg<0>
: Code<1> + Code<3> + Code<2> +
Reg<0> + "," + (Reg<0>+1)
+ "MOVE" + (Reg<0>+1) + "," + Reg<0>.
RULE
IntExpr ::= Ident
SEMANTICS
Label<0>=(Left<0>) ? 0 : 1;
Code<0>=(!Left<0>)
? "MOVE" + Reg<0> + "," + Val<1>
: Val<1>.
RULE
IntExpr ::= '(' IntExpr ')'
SEMANTICS
Label<0>=Label<2>;
Reg<2>=Reg<0>;
Code<0>=Code<2>.
RULE
Op ::= '+'
SEMANTICS
Code<0>="ADD".
RULE
Op ::= '-'
SEMANTICS
Code<0>="SUB".
RULE
Op ::= '*'
SEMANTICS
Code<0>="MUL".
RULE
Op ::= '/'
SEMANTICS
Code<0>="DIV".
|
Атрибутированное
дерево для
выражения
A*B+C*(D+E) приведено
на рис. 9.10. При
этом будет
сгенерирован
следующий
код:
MOVE B, R1
MUL A, R1
MOVE E, R2
ADD D, R2
MUL C, R2
ADD R1, R2
MOVE R2, R1
|
Приведенная
атрибутная
схема
требует
двух
проходов
по дереву
выражения.
Рассмотрим
теперь
другую
атрибутную
схему, в
которой
достаточно
одного
обхода для
генерация
программы
для
выражений с
оптимальным
распределением
регистров [7].
Пусть мы
произвели
разметку
дерева
разбора
так же,
как и в
предыдущем
алгоритме.
Назначение
регистров
будем
производить
следующим
образом.
Левому
потомку
всегда
назначается
регистр,
равный его
метке, а
правому -
его метке,
если она
не равна
метке его
левого
брата, и
метке + 1,
если метки
равны.
Поскольку
более
сложное
поддерево
всегда
вычисляется
раньше
более
простого,
его регистр
результата
имеет
больший
номер,
чем любой
регистр,
используемый
при
вычислении
более
простого
поддерева,
что
гарантирует
правильность
использования
регистров.
Приведенные
соображения
реализуются
следующей
атрибутной
схемой:
RULE
Expr ::= IntExpr
SEMANTICS
Code<0>=Code<1>; Left<1>=true.
RULE
IntExpr ::= IntExpr Op IntExpr
SEMANTICS
Left<1>=true; Left<3>=false;
Label<0>=(Label<1>==Label<3>)
? Label<1>+1
: Max(Label<1>,Label<3>);
Code<0>=(Label<3> > Label<1>)
? (Label<1>==0)
? Code<3> + Code<2> + Code<1>
+ "," + Label<3>
: Code<3> + Code<1> + Code<2> +
Label<1> + "," + Label<3>
: (Label<3> < Label<1>)
? Code<1> + Code<3> + Code<2> +
Label<1> + "," + Label<3> +
"MOVE" + Label<3> + "," + Label<1>
: // метки равны
Code<3> + "MOVE" + Label<3> +
"," + Label<3>+1 + Code<1> +
Code<2> + Label<1> + "," +
Label<1>+1.
RULE
IntExpr ::= Ident
SEMANTICS
Label<0>=(Left<0>) ? 0 : 1;
Code<0>=(Left<0>) ? Val<1>
: "MOVE" + Val<1> + "R1".
RULE
IntExpr ::= '(' IntExpr ')'
SEMANTICS
Label<0>=Label<2>;
Code<0>=Code<2>.
RULE
Op ::= '+'
SEMANTICS
Code<0>="ADD".
RULE
Op ::= '-'
SEMANTICS
Code<0>="SUB".
RULE
Op ::= '*'
SEMANTICS
Code<0>="MUL".
RULE
Op ::= '/'
SEMANTICS
Code<0>="DIV".
|
Команды
пересылки
требуются
для
согласования
номеров
регистров,
в которых
осуществляется
выполнение
операции, с
регистрами,
в которых
должен
быть выдан
результат.
Это имеет
смысл,
когда эти
регистры
разные.
Получиться
это может
из-за того,
что по
приведенной
схеме
результат
выполнения
операции
всегда
находится
в регистре
с номером
метки,
а метки
левого и
правого
поддеревьев
могут
совпадать.
Для
выражения
A*B+C*(D+E) будет
сгенерирован
следующий
код:
MOVE E, R1
ADD D, R1
MUL C, R1
MOVE R1, R2
MOVE B, R1
MUL A, R1
ADD R1, R2
|
В приведенных
атрибутных
схемах
предполагалось,
что
регистров
достаточно
для
трансляции
любого
выражения.
Если это
не так,
приходится
усложнять
схему
трансляции
и при
необходимости
сбрасывать
содержимое
регистров в
память (или
магазин).
9.7 Трансляция
логических
выражений
Логические
выражения,
включающие
логическое
умножение,
логическое
сложение и
отрицание,
можно
вычислять
как
непосредственно,
используя
таблицы
истинности,
так и с
помощью
условных
выражений,
основанных
на следующих
простых
правилах:
| A AND B | эквивалентно | if A then B else False, |
| A OR B | эквивалентно | if A then True else B. |
|
Если в
качестве
компонент
выражений
могут
входить
функции с
побочным
эффектом,
то, вообще
говоря,
результат
вычисления
может
зависеть
от способа
вычисления.
В некоторых
языках
программирования
не оговаривается,
каким
способом
должны
вычисляться
логические
выражения
(например, в
Паскале), в
некоторых
требуется,
чтобы
вычисления
производились
тем или иным
способом
(например,
в Модуле-2
требуется,
чтобы
выражения
вычислялись
по приведенным
формулам), в
некоторых
языках есть
возможность
явно задать
способ
вычисления
(Си, Ада).
Вычисление
логических
выражений
непосредственно
по таблицам
истинности
аналогично
вычислению
арифметических
выражений,
поэтому мы
не будем их
рассматривать
отдельно.
Рассмотрим
подробнее
способ
вычисления
с помощью
приведенных
выше формул
(будем
называть
его
«вычислением
с условными
переходами»).
Иногда
такой
способ
рассматривают
как
оптимизацию
вычисления
логических
выражений.
Рассмотрим
следующую
атрибутную
грамматику
со входным
языком
логических
выражений:
RULE
Expr ::= BoolExpr
SEMANTICS
FalseLab<1>=False; TrueLab<1>=True;
Code<0>=Code<1>.
RULE
BoolExpr ::= BoolExpr 'AND' BoolExpr
SEMANTICS
FalseLab<1>=FalseLab<0>; TrueLab<1>=NodeLab<3>;
FalseLab<3>=FalseLab<0>; TrueLab<3>=TrueLab<0>;
Code<0>=NodeLab<0> + ":" + Code<1> + Code<3>.
RULE
BoolExpr ::= BoolExpr 'OR' BoolExpr
SEMANTICS
FalseLab<1>=NodeLab<3>; TrueLab<1>=TrueLab<0>;
FalseLab<3>=FalseLab<0>; TrueLab<3>=TrueLab<0>;
Code<0>=NodeLab<0> + ":" + Code<1> + Code<3>.
RULE
BoolExpr ::= '(' BoolExpr ')'
SEMANTICS
FalseLab<2>=FalseLab<0>;
TrueLab<2>=TrueLab<0>;
Code<0>=NodeLab<0> + ":" + Code<2>.
RULE
BoolExpr ::= F
SEMANTICS
Code<0>=NodeLab<0> + ":" + "GOTO" + FalseLab<0>.
RULE
BoolExpr ::= T
SEMANTICS
Code<0>=NodeLab<0> + ":" + "GOTO" + TrueLab<0>.
|
Здесь
предполагается,
что все
вершины
дерева
занумерованы
и номер
вершины
дает
атрибут
NodeLab. Метки
вершин
передаются,
как это
изображено
на рис. 9.11.
Таким
образом,
каждому
атрибутированному
дереву
в этой
атрибутной
грамматике
сопоставляется
код,
полученный
в результате
обхода
дерева
сверху-вниз
слева-направо
следующим
образом.
При входе
в вершину BoolExpr
генерируется
ее номер, в
вершине F
генерируется
текст GOTO
значение
атрибута FalseLab<0>,
в вершине T
- GOTO значение
атрибута TrueLab<0>.
Например,
для
выражения
F OR ( F AND T AND T ) OR T
|
получим
атрибутированное
дерево,
изображенное
на рис. 9.12, и
код
1:7: GOTO 2
2:8:4:9: GOTO 3
5:10: GOTO 6
6: GOTO True
3: GOTO True
True: ...
False: ...
|
Эту
линеаризованную
запись
можно
трактовать
как
программу
вычисления
логического
значения:
каждая
строка
может быть
помечена
номером
вершины и
содержать
либо
переход
на другую
строку, либо
переход на
True или False, что
соответствует
значению
выражения
true или false. Будем
говорить,
что
полученная
программа
вычисляет
(или
интерпретирует)
значение
выражения,
если в
результате
ее выполнения
(от первой
строки)
мы придем
к строке,
содержащей
GOTO True или GOTO False.
Утверждение 9.1. В
результате
интерпретации
поддерева с
некоторыми
значениями
атрибутов
FalseLab и TrueLab в его
корне
выполняется
команда
GOTO TrueLab, если
значение
выражения
истинно, и
команда
GOTO FalseLab, если
значение
выражения
ложно.
Доказательство. Применим
индукцию
по высоте
дерева. Для
деревьев
высоты 1,
соответствующих
правилам
BoolExpr ::= F и BoolExpr ::= T,
справедливость
утверждения
следует из
соответствующих
атрибутных
правил.
Пусть
дерево
имеет
высоту n > 1.
Зависимость
атрибутов
для
дизъюнкции
и конъюнкции
приведена
на рис. 9.13.
Если для
конъюнкции
значение
левого
поддерева
ложно и по
индукции
вычисление
левого
поддерева
завершается
командой GOTO FalseLab<1>,
то получаем,
что
вычисление
всего
дерева
завершается
командой
перехода GOTO FalseLab<0>
(= FalseLab<1>). Если же
значение
левого
поддерева
истинно,
то его
вычисление
завершается
командой
перехода
GOTO TrueLab<1> (= NodeLab<3>). Если
значение
правого
поддерева
ложно, то
вычисление
всего
дерева
завершается
командой
GOTO FalseLab<0> (= FalseLab<3>). Если
же оно
истинно,
вычисление
всего
дерева
завершается
командой
перехода
GOTO TrueLab<0> (= TrueLab<3>).
Аналогично
- для
дизъюнкции._
Утверждение 9.2. Для
любого
логического
выражения,
состоящего
из констант,
программа,
полученная
в результате
обхода
дерева
этого
выражения,
завершается
со значением
логического
выражения
в обычной
интерпретации,
т.е. осуществляется
переход
на True для
значения,
равного true, и
переход на
метку False для
значения
false.
Доказательство. Это
утверждение
является
частным
случаем
предыдущего.
Его
справедливость
следует
из того,
что метки
корня
дерева
равны
соответственно
TrueLab = True и FalseLab = False. _
Добавим
теперь
новое
правило в
предыдущую
грамматику:
RULE
BoolExpr ::= Ident
SEMANTICS
Code<0>=NodeLab<0> + ":" + "if (" + Val<1> + "==T) GOTO" +
TrueLab<0> + "else GOTO" + FalseLab<0>.
|
Тогда,
например,
для
выражения
A OR ( B AND C AND D ) OR E получим
следующую
программу:
1:7: if (A==T) GOTO True else GOTO 2
2:8:4:9: if (B==T) GOTO 5 else GOTO 3
5:10: if (C==T) GOTO 6 else GOTO 3
6: if (D==T) GOTO True else GOTO 3
3: if (E==T) GOTO True else GOTO False
True: ...
False: ...
|
При каждом
конкретном
наборе
данных эта
программа
превращается
в программу
вычисления
логического
значения.
Утверждение 9.3. В каждой
строке
программы,
сформированной
предыдущей
атрибутной
схемой, одна
из меток
внутри
условного
оператора
совпадает
с меткой
следующей
строки.
Доказательство. Действительно,
по правилам
наследования
атрибутов
TrueLab и FalseLab, в
правилах
для
дизъюнкции
и конъюнкции
либо
атрибут
FalseLab, либо
атрибут TrueLab
принимает
значение
метки
следующего
поддерева.
Кроме
того, как
значение
FalseLab, так и
значение TrueLab,
передаются
в правое
поддерево
от предка.
Таким
образом,
самый
правый
потомок
всегда
имеет
одну из
меток TrueLab или
FalseLab, равную
метке
правого
брата
соответствующего
поддерева.
Учитывая
порядок
генерации
команд,
получаем
справедливость
утверждения._
Дополним
теперь
атрибутную
грамматику
следующим
образом:
RULE
Expr ::= BoolExpr
SEMANTICS
FalseLab<1>=False; TrueLab<1>=True;
Sign<1>=false;
Code<0>=Code<1>.
RULE
BoolExpr ::= BoolExpr 'AND' BoolExpr
SEMANTICS
FalseLab<1>=FalseLab<0>; TrueLab<1>=NodeLab<3>;
FalseLab<3>=FalseLab<0>; TrueLab<3>=TrueLab<0>;
Sign<1>=false; Sign<3>=Sign<0>;
Code<0>=NodeLab<0> + ":" + Code<1> + Code<3>.
RULE
BoolExpr ::= BoolExpr 'OR' BoolExpr
SEMANTICS
FalseLab<1>=NodeLab<3>; TrueLab<1>=TrueLab<0>;
FalseLab<3>=FalseLab<0>; TrueLab<3>=TrueLab<0>;
Sign<1>=true; Sign<3>=Sign<0>;
Code<0>=NodeLab<0> + ":" + Code<1> + Code<3>.
RULE
BoolExpr ::= 'NOT' BoolExpr
SEMANTICS
FalseLab<2>=TrueLab<0>; TrueLab<2>=FalseLab<0>;
Sign<2>=! Sign<0>;
Code<0>=Code<2>.
RULE
BoolExpr ::= '(' BoolExpr ')'
SEMANTICS
FalseLab<2>=FalseLab<0>;
TrueLab<2>=TrueLab<0>;
Sign<2>=Sign<0>;
Code<0>=NodeLab<0> + ":" + Code<2>.
RULE
BoolExpr ::= F
SEMANTICS
Code<0>=NodeLab<0> + ":" + "GOTO" + FalseLab<0>.
RULE
BoolExpr ::= T
SEMANTICS
Code<0>=NodeLab<0> + ":" + "GOTO" + TrueLab<0>.
RULE
BoolExpr ::= Ident
SEMANTICS
Code<0>=NodeLab<0> + ":" + "if (" + Val<1> + "==T) GOTO"
+ TrueLab<0> + "else GOTO" + FalseLab<0>.
|
Правила
наследования
атрибута Sign
приведены
на рис. 9.14.
Программу
желательно
сформировать
таким
образом,
чтобы
else-метка
была как
раз меткой
следующей
вершины.
Как это
можно
сделать,
следует из
следующего
утверждения.
Утверждение 9.4. В каждой
терминальной
вершине,
метка
ближайшего
правого
для нее
поддерева
равна
значению
атрибута
FalseLab этой
вершины,
тогда и
только
тогда, когда
значение
атрибута Sign
этой вершины
равно true, и
наоборот,
метка
ближайшего
правого
для нее
поддерева
равна
значению
атрибута
TrueLab этой
вершины,
тогда и
только
тогда, когда
значение
атрибута Sign
равно false.
Доказательство. Действительно,
если
ближайшей
общей
вершиной
является AND,
то в левого
потомка
передается
NodeLab правого
потомка в
качестве TrueLab и
одновременно
Sign правого
потомка
равен true.
Если же
ближайшей
общей
вершиной
является OR,
то в левого
потомка
передается
NodeLab правого
потомка в
качестве FalseLab и
одновременно
Sign правого
потомка
равен false.
Во все же
правые
потомки
значения
TrueLab, FalseLab и Sign
передаются
из предка (за
исключением
правила
для NOT, в
котором TrueLab и
FalseLab меняются
местами, но
одновременно
на противоположный
меняется
и Sign). _
Эти два
утверждения
(3 и 4) позволяют
заменить
последнее
правило
атрибутной
грамматики
следующим
образом:
RULE
BoolExpr ::= Ident
SEMANTICS
Code<0>=NodeLab<0> + ":" +
(Sign<0>
? "if (" + Val<1> + "==T) GOTO" + TrueLab<0>
: "if (" + Val<1> + "==F) GOTO" + FalseLab<0>).
|
В свою
очередь, при
генерации
машинных
команд это
правило
можно
заменить на
следующее:
RULE
BoolExpr ::= Ident
SEMANTICS
Code<0>=NodeLab<0> + ":" + "TST" + Val<1> +
(Sign<0>
? "BNE" + TrueLab<0>
: "BEQ" + FalseLab<0>).
|
Таким
образом, для
выражения
A OR ( B AND C AND D ) OR E получим
следующий
код на
командах
перехода:
1:7: TST A
BNE True
2:8:4:9: TST B
BEQ 3
5:10: TST C
BEQ 3
6: TST D
BNE True
3: TST E
BEQ False
True: ...
False: ...
|
Если
элементом
логического
выражения
является
сравнение,
то генерируется
команда,
соответствующая
знаку
сравнения
(BEQ для =, BNE для
<>, BGE для >= и
т.д.), если
атрибут Sign
соответствующей
вершины
имеет
значение true, и
отрицание
(BNE для =, BEQ для
<>, BLT для >= и
т.д.), если
атрибут
Sign имеет
значение
false.
9.8 Выделение
общих
подвыражений
Выделение
общих
подвыражений
относится
к области
оптимизации
программ.
В общем
случае
трудно
(или даже
невозможно)
провести
границу
между
оптимизацией
и «качественной
трансляцией».
Оптимизация
- это и есть
качественная
трансляция.
Обычно
термин
«оптимизация»
употребляют,
когда для
повышения
качества
программы
используют
ее глубокие
преобразования
такие,
например,
как перевод
в графовую
форму для
изучения
нетривиальных
свойств
программы.
В этом
смысле
выделение
общих
подвыражений
- одна из
простейших
оптимизаций.
Для ее
осуществления
требуется
некоторое
преобразование
программы,
а именно
построение
ориентированного
ациклического
графа, о
котором
говорилось
в главе,
посвященной
промежуточным
представлениям.
Линейный
участок - это
последовательность
операторов,
в которую
управление
входит в
начале и
выходит в
конце без
остановки
и перехода
изнутри.
Рассмотрим
дерево
линейного
участка,
в котором
вершинами
служат
операции, а
потомками
- операнды.
Будем
говорить,
что две
вершины
образуют
общее
подвыражение,
если
поддеревья
для них
совпадают,
т.е. имеют
одинаковую
структуру и,
соответственно,
одинаковые
операции во
внутренних
вершинах и
одинаковые
операнды
в листьях.
Выделение
общих
подвыражений
позволяет
генерировать
для них код
один раз,
хотя может
привести и
к некоторым
трудностям,
о чем
вкратце
будет
сказано
ниже.
Выделение
общих
подвыражений
проводится
на линейном
участке и
основывается
на двух
положениях.
1. Поскольку
на линейном
участке
переменной
может быть
несколько
присваиваний,
то при
выделении
общих
подвыражений
необходимо
различать
вхождения
переменных
до и после
присваивания.
Для этого
каждая
переменная
снабжается
счетчиком.
Вначале
счетчики
всех
переменных
устанавливаются
равными 0.
При каждом
присваивании
переменной
ее счетчик
увеличивается
на 1.
2. Выделение
общих
подвыражений
осуществляется
при обходе
дерева
выражения
снизу
вверх
слева
направо. При
достижении
очередной
вершины
(пусть
операция,
примененная
в этой
вершине,
есть
бинарная
op; в случае
унарной
операции
рассуждения
те же)
просматриваем
общие
подвыражения,
связанные
с op. Если
имеется
выражение,
связанное
с op и такое,
что его
левый
операнд
есть общее
подвыражение
с левым
операндом
нового
выражения,
а правый
операнд
- общее
подвыражение
с правым
операндом
нового
выражения,
то объявляем
новое
выражение
общим с
найденным
и в новом
выражении
запоминаем
указатель
на найденное
общее
выражение.
Базисом
построения
служит
переменная:
если
операндами
обоих
выражений
являются
одинаковые
переменные
с одинаковыми
счетчиками,
то они
являются
общими
подвыражениями.
Если
выражение
не выделено
как
общее, оно
заносится
в список
операций,
связанных
с op.
Рассмотрим
теперь
реализацию
алгоритма
выделения
общих
подвыражений.
Поддерживаются
следующие
глобальные
переменные:
Table - таблица
переменных;
для каждой
переменной
хранится ее
счетчик (Count) и
указатель
на вершину
дерева
выражений,
в которой
переменная
встретилась
в последний
раз в правой
части (Last);
OpTable - таблица
списков
(типа LisType)
общих
подвыражений,
связанных
с каждой
операцией.
Каждый
элемент
списка
хранит
указатель
на вершину
дерева
(поле Addr) и
продолжение
списка
(поле List).
С каждой
вершиной
дерева
выражения
связана
запись
типа NodeType, со
следующими
полями:
Left - левый
потомок
вершины,
Right - правый
потомок
вершины,
Comm - указатель
на предыдущее
общее
подвыражение,
Flag - признак,
является ли
поддерево
общим
подвыражением,
Varbl - признак,
является
ли вершина
переменной,
VarCount - счетчик
переменной.
Выделение
общих
подвыражений
и построение
дерева
осуществляются
приведенными
ниже
правилами.
Атрибут Entry
нетерминала
Variable дает
указатель
на переменную
в таблице
Table. Атрибут
Val символа Op
дает код
операции.
Атрибут Node
символов
IntExpr и Assignment дает
указатель
на запись
типа NodeType
соответствующего
нетерминала.
RULE
Assignment ::= Variable IntExpr
SEMANTICS
Table[Entry<1>].Count=Table[Entry<1>].Count+1.
// Увеличить счетчик присваиваний переменной
RULE
IntExpr ::= Variable
SEMANTICS
if ((Table[Entry<1>].Last!=NULL)
// Переменная уже была использована
&& (Table[Entry<1>].Last->VarCount
== Table[Entry<1>].Count ))
// С тех пор переменной не было присваивания
{Node<0>->Flag=true;
// Переменная - общее подвыражение
Node<0>->Comm= Table[Entry<1>].Last;
// Указатель на общее подвыражение
}
else Node<0>->Flag=false;
Table[Entry<1>].Last=Node<0>;
// Указатель на последнее использование переменной
Node<0>->VarCount= Table[Entry<1>].Count;
// Номер использования переменной
Node<0>->Varbl=true.
// Выражение - переменная
RULE
IntExpr ::= Op IntExpr IntExpr
SEMANTICS
LisType * L; //Тип списков операции
if ((Node<2>->Flag) && (Node<3>->Flag))
// И справа, и слева - общие подвыражения
{L=OpTable[Val<1>];
// Начало списка общих подвыражений для операции
while (L!=NULL)
if ((Node<2>==L->Left)
&& (Node<3>==L->Right))
// Левое и правое поддеревья совпадают
break;
else L=L->List;// Следующий элемент списка
}
else L=NULL; //Не общее подвыражение
Node<0>->Varbl=false; // Не переменная
Node<0>->Comm=L;
//Указатель на предыдущее общее подвыражение или NULL
if (L!=NULL)
{Node<0>->Flag=true; //Общее подвыражение
Node<0>->Left=Node<2>;
// Указатель на левое поддерево
Node<0>->Right=Node<3>;
// Указатель на правое поддерево
}
else {Node<0>->Flag=false;
// Данное выражение не может рассматриваться как общее
// Если общего подвыражения с данным не было,
// включить данное в список для операции
L=alloc(sizeof(struct LisType));
L->Addr=Node<0>;
L->List=OpTable[Val<1>];
OpTable[Val<1>]=L;
}.
|
Рассмотрим
теперь
некоторые
простые
правила
распределения
регистров
при наличии
общих
подвыражений.
Если число
регистров
ограничено,
можно
выбрать
один из
следующих
двух
вариантов.
1. При
обнаружении
общего
подвыражения
с подвыражением
в уже
просмотренной
части
дерева (и,
значит, с уже
распределенными
регистрами)
проверяем,
расположено
ли его
значение на
регистре.
Если да,
и если
регистр
после
этого не
менялся,
заменяем
вычисление
поддерева
на значение
в регистре.
Если
регистр
менялся, то
вычисляем
подвыражение
заново.
2. Вводим
еще один
проход.
На первом
проходе
распределяем
регистры.
Если в
некоторой
вершине
обнаруживается,
что ее
поддерево
общее с уже
вычисленным
ранее, но
значение
регистра
потеряно,
то в такой
вершине
на втором
проходе
необходимо
сгенерировать
команду
сброса
регистра
в рабочую
память.
Выигрыш
в коде
будет, если
стоимость
команды
сброса
регистра
+ доступ к
памяти в
повторном
использовании
этой
памяти не
превосходит
стоимости
заменяемого
поддерева.
Поскольку
стоимость
команды MOVE
известна,
можно
сравнить
стоимости
и принять
оптимальное
решение:
пометить
предыдущую
вершину для
сброса либо
вычислять
поддерево
полностью.
9.9 Генерация
оптимального
кода
методами
синтаксического
анализа
9.9.1 Сопоставление
образцов
Техника
генерации
кода,
рассмотренная
выше,
основывалась
на однозначном
соответствии
структуры
промежуточного
представления
и описывающей
это
представление
грамматики.
Недостатком
такого
«жесткого»
подхода
является
то, что как
правило
одну и ту же
программу
на промежуточном
языке
можно
реализовать
многими
различными
способами
в системе
команд
машины.
Эти разные
реализации
могут
иметь
различную
длину,
время
выполнения
и другие
характеристики.
Для
генерации
более
качественного
кода
может быть
применен
подход,
изложенный
в настоящей
главе.
Этот
подход
основан на
понятии
«сопоставления
образцов»:
командам
машины
сопоставляются
некоторые
«образцы»,
вхождения
которых
ищутся в
промежуточном
представлении
программы,
и делается
попытка
«покрыть»
промежуточную
программу
такими
образцами.
Если это
удается, то
по образцам
восстанавливается
программа
уже в кодах.
Каждое
такое
покрытие
соответствует
некоторой
программе,
реализующей
одно и то же
промежуточное
представление.
На рис. 9.15
показано
промежуточное
дерево для
оператора
a = b[i] + 5, где a, b, i -
локальные
переменные,
хранимые со
смещениями x, y, z
соответственно
в областях
данных с
одноименными
адресами.
Элемент
массива b
занимает
память
в одну
машинную
единицу.
0-местная
операция const
возвращает
значение
атрибута
соответствующей
вершины
промежуточного
дерева,
указанного
на рисунке
в скобках
после
оператора.
Одноместная
операция @
означает
косвенную
адресацию и
возвращает
содержимое
регистра
или ячейки
памяти,
имеющей
адрес,
задаваемый
аргументом
операции.
На рис. 9.16
показан
пример
сопоставления
образцов
машинным
командам.
Приведены
два
варианта
задания
образца:
в виде
дерева
и в виде
правила
контекстно-свободной
грамматики.
Для каждого
образца
указана
машинная
команда,
реализующая
этот
образец, и
стоимость
этой
команды.
В каждом
дереве-образце
корень
или лист
может быть
помечен
терминальным
и/или
нетерминальным
символом.
Внутренние
вершины
помечены
терминальными
символами
- знаками
операций.
При
наложении
образца
на дерево
выражения,
во-первых,
терминальный
символ
образца
должен
соответствовать
терминальному
символу
дерева, и,
во-вторых,
образцы
должны
«склеиваться»
по типу
нетерминального
символа, т.е.
тип корня
образца
должен
совпадать
с типом
вершины,
в которую
образец
подставляется
корнем.
Допускается
использование
«цепных»
образцов,
т.е. образцов,
корню
которых не
соответствует
терминальный
символ, и
имеющих
единственный
элемент
в правой
части.
Цепные
правила
служат для
приведения
вершин к
одному типу.
Например, в
рассматриваемой
системе
команд
одни и те же
регистры
используются
как для
целей
адресации,
так и для
вычислений.
Если бы в
системе
команд для
этих целей
использовались
разные
группы
регистров,
то в
грамматике
команд
могли бы
использоваться
разные
нетерминалы,
а для
пересылки
из адресного
регистра
в регистр
данных
могла бы
использоваться
соответствующая
команда и
образец.
Нетерминалы
Reg на образцах
могут быть
помечены
индексом
(i или j), что
(неформально)
соответствует
номеру
регистра
и служит
лишь для
пояснения
смысла
использования
регистров.
Отметим,
что при
генерации
кода
рассматриваемым
методом не
осуществляется
распределение
регистров.
Это
является
отдельной
задачей.
Стоимость
может
определяться
различными
способами,
например
числом
обращений к
памяти при
выборке и
исполнении
команды.
Здесь мы не
рассматриваем
этого
вопроса.
На рис. 9.17
приведен
пример
покрытия
промежуточного
дерева рис. 9.15
образцами
рис. 9.16. В
рамки
заключены
фрагменты
дерева,
сопоставленные
образцу
правила,
номер
которого
указывается
в левом
верхнем
углу рамки. В
квадратных
скобках
указаны
результирующие
вершины.
Приведенное
покрытие
дает такую
последовательность
команд:
MOVE b,Rb
ADD #y,Rb
MOVE i,Ri
ADD z(Ri),Rb
MOVE (Rb),Rb
ADD #5,Rb
MOVE a,Ra
MOVE Rb,x(Ra)
|
Основная
идея
подхода
заключается
в том, что
каждая
команда
машины
описывается
в виде
такого
образца.
Различные
покрытия
дерева
промежуточного
представления
соответствуют
различным
последовательностям
машинных
команд.
Задача
выбора
команд
состоит в
том, чтобы
выбрать
наилучший
способ
реализации
того или
иного
действия
или
последовательности
действий, т.
е. выбрать в
некотором
смысле
оптимальное
покрытие.
Для выбора
оптимального
покрытия
было
предложено
несколько
интересных
алгоритмов,
в частности
использующих
динамическое
программирование [11,
13]. Мы здесь
рассмотрим
алгоритм [12],
комбинирующий
возможности
синтаксического
анализа и
динамического
программирования.
В основу
этого
алгоритма
положен
синтаксический
анализ
неоднозначных
грамматик
(модифицированный
алгоритм
Кока, Янгера
и Касами [15, 16]),
эффективный
в реальных
приложениях.
Этот же
метод
может быть
применен
и тогда,
когда в
качестве
промежуточного
представления
используется
дерево.
9.9.2 Синтаксический
анализ для
T-грамматик
Обычно код
генерируется
из некоторого
промежуточного
языка с
довольно
жесткой
структурой.
В частности,
для каждой
операции
известна ее
размерность,
то есть
число
операндов,
большее
или равное
0. Операции
задаются
терминальными
символами,
и наоборот
- будем
считать все
терминальные
символы
знаками
операций.
Назовем
грамматики,
удовлетворяющие
этим
ограничениям,
T-грамматиками.
Правая
часть
каждой
продукции в
Т-грамматике
есть
правильное
префиксное
выражение,
которое
может быть
задано
следующим
определением:
- Операция
размерности
0 является
правильным
префиксным
выражением;
- Нетерминал
является
правильным
префиксным
выражением;
- Префиксное
выражение,
начинающееся
со знака
операции
размерности
n > 0, является
правильным,
если после
знака операции
следует
n правильных
префиксных
выражений;
- Ничто другое
не является
правильным
префиксным
выражением.
Образцы,
соответствующие
машинным
командам,
задаются
правилами
грамматики
(вообще
говоря,
неоднозначной).
Генератор
кода
анализирует
входное
префиксное
выражение
и строит
одновременно
все
возможные
деревья
разбора.
После
окончания
разбора
выбирается
дерево с
наименьшей
стоимостью.
Затем
по этому
единственному
оптимальному
дереву
генерируется
код.
Для
T-грамматик
все цепочки,
выводимые
из любого
нетерминала
A, являются
префиксными
выражениями
с фиксированной
арностью
операций.
Длины всех
выражений
из входной
цепочки
a1...an можно
предварительно
вычислить
(под длиной
выражения
имеется
ввиду
длина
подстроки,
начинающейся
с символа
кода
операции и
заканчивающейся
последним
символом,
входящим в
выражение
для этой
операции).
Поэтому
можно
проверить,
сопоставимо
ли некоторое
правило с
подцепочкой
ai...ak входной
цепочки a1...an,
проходя
слева-направо
по ai...ak. В
процессе
прохода по
цепочке
предварительно
вычисленные
длины
префиксных
выражений
используются
для того,
чтобы
перейти
от одного
терминала к
следующему
терминалу,
пропуская
подцепочки,
соответствующие
нетерминалам
правой
части
правила.
Цепные
правила не
зависят от
операций,
следовательно,
их необходимо
проверять
отдельно.
Применение
одного
цепного
правила
может
зависеть от
применения
другого
цепного
правила.
Следовательно,
применение
цепных
правил
необходимо
проверять
до тех
пор, пока
нельзя
применить
ни одно
из цепных
правил. Мы
предполагаем,
что в
грамматике
нет циклов в
применении
цепных
правил.
Построение
всех
вариантов
анализа для
T-грамматики
дано ниже в
алгоритме
9.1. Тип Titem в
алгоритме
9.1 ниже
служит для
описания
ситуаций
(т.е. правил
вывода и
позиции
внутри
правила).
Тип Tterminal -
это тип
терминального
символа
грамматики,
тип Tproduction -
тип для
правила
вывода.
Алгоритм
9.1
Tterminal a[n];
setofTproduction r[n];
int l[n]; // l[i] - длина a[i]-выражения
Titem h; // используется при поиске правил,
// сопоставимых с текущей подцепочкой
// Предварительные вычисления
Для каждой позиции i вычислить длину a[i]-выражения l[i];
// Распознавание входной цепочки
for (int i=n-1;i>=0;i-){
for (каждого правила A -> a[i] y из P){
j=i+1;
if (l[i]>1)
// Первый терминал a[i] уже успешно сопоставлен
{h=[A->a[i].y];
do // найти a[i]y, сопоставимое с a[i]..a[i+l[i]-1]
{Пусть h==[A->u.Xv];
if (X in T)
if (X==a[j]) j=j+1; else break;
else // X in N
if (имеется X->w in r[j]) j=j+l[j]; else break;
h=[A->uX.v];
//перейти к следующему символу
}
while (j!=i+l[i]);
} // l[i]>1
if (j==i+l[i]) r[i]=r[i] + { (A->a[i]y) }
} // for по правилам A -> a[i] y
// Сопоставить цепные правила
while (существует правило C->A из P такое, что
имеется некоторый элемент (A->w) в r[i]
и нет элемента (C->A) в r[i])
r[i]=r[i] + { (C->A) };
} // for по i
Проверить, принадлежит ли (S->w) множеству r[0];
|
Множества
r[i] имеют
размер
O(|P|). Можно
показать,
что
алгоритм
имеет
временную
и емкостную
сложность
O(n).
Рассмотрим
вновь
пример
рис. 9.15. В
префиксной
записи
приведенный
фрагмент
программы
записывается
следующим
образом:
= + a x + @ + + b y @ + i z 5
|
На рис. 9.18
приведен
результат
работы
алгоритма.
Правила
вычисления
стоимости
приведены
в следующем
разделе. Все
возможные
выводы
входной
цепочки
(включая
оптимальный)
можно
построить,
используя
таблицу l
длин
префиксных
выражений
и таблицу r
применимых
правил.
Пусть G - это
T-грамматика.
Для каждой
цепочки z
из L(G) можно
построить
абстрактное
синтаксическое
дерево
соответствующего
выражения
(рис. 9.15). Мы
можем
переписать
алгоритм
так, чтобы
он принимал
на входе
абстрактное
синтаксическое
дерево
выражения, а
не цепочку.
Этот
вариант
алгоритма
приведен
ниже. В этом
алгоритме
дерево
выражения
обходится
сверху
вниз и в
нем ищутся
поддеревья,
сопоставимые
с правыми
частями
правил
из G. Обход
дерева
осуществляется
процедурой
PARSE. После
обхода
поддерева
данной
вершины
в ней
применяется
процедура
MATCHED, которая
пытается
найти все
образцы,
сопоставимые
поддереву
данной
вершины.
Для этого
каждое
правило-образец
разбивается
на компоненты
в соответствии
с встречающимися
в нем
операциями.
Дерево
обходится
справа
налево
только для
того, чтобы
иметь
соответствие
с порядком
вычисления
в алгоритме
9.1. Очевидно,
что можно
обходить
дерево
вывода
и слева
направо.
Структура
данных,
представляющая
вершину
дерева,
имеет
следующую
форму:
struct Tnode {
Tterminal op;
Tnode * son[MaxArity];
setofTproduction RULEs;
};
|
В комментариях
указаны
соответствующие
фрагменты
алгоритма
9.1.
Алгоритм
9.2
Tnode * root;
bool MATCHED(Tnode * n, Titem h)
{ bool matching;
пусть h==[A->u.Xvy], v== v_1 v_2 ... v_m, m=Arity(X);
if (X in T)// сопоставление правила
if (m==0) // if l[i]==1
if (X==n->op) //if X==a[j]
return(true);
else
return(false);
else // if l[i]>1
if (X==n->op) //if X==a[j]
{matching=true;
for (i=1;i<=m;i++) //j=j+l[j]
matching=matching && //while (j==i+l[i])
MATCHED(n->son[i-1],[A->uXv'.v_i v"y]);
return(matching); //h=[A->uX.v]
}
else
return(false);
else // X in N поиск подвывода
if (в n^.RULEs имеется правило с левой частью X)
return(true);
else
return(false);
}
void PARSE(Tnode * n)
{
for (i=Arity(n->op);i>=1;i-)
// for (i=n; i>=1;i-)
PARSE(n->son[i-1]);
n->RULEs=EMPTY;
for (каждого правила A->bu из P такого, что b==n->op)
if (MATCHED(n,[A->.bu])) //if (j==i+l[i])
n->RULEs=n->RULEs+{(A->bu)};
// Сопоставление цепных правил
while (существует правило C->A из P такое, что
некоторый элемент (A->w) в n->RULEs
и нет элемента (C->A) в n->RULEs)
n->RULEs=n->RULEs+{(C->A)};
}
Основная программа
// Предварительные вычисления
Построить дерево выражения для входной цепочки z;
root = указатель дерева выражения;
// Распознать входную цепочку
PARSE(root);
Проверить, входит ли во множество root->RULEs
правило с левой частью S;
|
Выходом
алгоритма
является
дерево
выражения
для z,
вершинам
которого
сопоставлены
применимые
правила.
С помощью
такого
дерева
можно
построить
все
выводы для
исходного
префиксного
выражения.
9.9.3 Выбор
дерева
вывода
наименьшей
стоимости
T-грамматики,
описывающие
системы
команд,
обычно
являются
неоднозначными.
Чтобы
сгенерировать
код для
некоторой
входной
цепочки,
необходимо
выбрать
одно из
возможных
деревьев
вывода.
Это дерево
должно
представлять
желаемое
качество
кода,
например
размер
кода и/или
время
выполнения.
Для выбора
дерева из
множества
всех
построенных
деревьев
вывода
можно
использовать
атрибуты
стоимости,
атрибутные
формулы,
вычисляющие
их значения,
и критерии
стоимости,
которые
оставляют
для каждого
нетерминала
единственное
применимое
правило.
Атрибуты
стоимости
сопоставляются
всем
нетерминалам,
атрибутные
формулы
- всем
правилам
T-грамматики.
Предположим,
что для
вершины n
обнаружено
применимое
правило
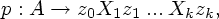
где z
i 
T
* для
0

i

k и X
j 
N для 1

j

k.
Вершина
n имеет
потомков
n
1, ..., n
k, которые
соответствуют
нетерминалам
X
1, ..., X
k. Значения
атрибутов
стоимости
вычисляются
обходя
дерево
снизу
вверх.
Вначале
атрибуты
стоимости
инициализируются
неопределенным
значением UndefinedValue.
Предположим,
что
значения
атрибутов
стоимости
для всех
потомков
n
1, ..., n
k вершины n
вычислены.
Если
правилу p
сопоставлена
формула
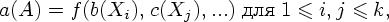
то
производится
вычисление
значения
атрибута a
нетерминала
A в вершине
n. Для всех
примененных
правил
ищется
такое,
которое
дает
минимальное
значение
стоимости.
Отсутствие
примененных
правил
обозначается
через Undefined,
значение
которого
полагается
большим
любого
определенного
значения.
Добавим в
алгоритм 9.2
реализацию
атрибутов
стоимости,
формул их
вычисления
и критериев
отбора. Из
алгоритма
можно
исключить
поиск
подвыводов,
соответствующих
правилам,
для которых
значение
атрибута
стоимости
не определено.
Структура
данных,
представляющая
вершину
дерева,
принимает
следующий
вид:
struct Tnode {
Tterminal op;
Tnode * son[MaxArity];
struct * { unsigned CostAttr;
Tproduction Production;
} nonterm [Tnonterminal];
OperatorAttributes ...
|
Тело
процедуры
PARSE принимает
вид
void PARSE(Tnode *n)
{for (i=Arity(n->op);i>=1;i-)
PARSE(n->son[i]);
for (каждого A из N)
{n->nonterm[A].CostAttr=UndefinedValue;
n->nonterm[A].production=Undefined;
}
for (каждого правила A->bu из P
такого, что b==n->op)
if (MATCHED(n,[A->.bu]))
{ВычислитьАтрибутыСтоимостиДля(A,n,(A->bu));
ПроверитьКритерийДля(A,n->nonterm[A].CostAttr);
if ((A->bu) лучше,
чем ранее обработанное правило для A)
{Модифицировать(n->nonterm[A].CostAttr);
n->nonterm[A].production=(A->bu);
}
}
// Сопоставить цепные правила
while (существует правило C->A из P, которое
лучше, чем ранее обработанное правило для A)
{ВычислитьАтрибутыСтоимостиДля(C,n,(C->A));
ПроверитьКритерийДля(C,n->nonterm[C].CostAttr);
if ((C->A) лучше)
{Модифицировать(n->nonterm[C].CostAttr);
n->nonterm[C].production=(C->A);
}
}
}
|
Дерево
наименьшей
стоимости
определяется
как дерево,
соответствующее
минимальной
стоимости
корня.
Когда
выбрано
дерево
вывода
наименьшей
стоимости,
вычисляются
значения
атрибутов,
сопоставленных
вершинам
дерева
вывода, и
генерируются
соответствующие
машинные
команды.
Вычисление
значений
атрибутов,
генерация
кода
осуществляются
в процессе
обхода
выбранного
дерева
вывода
сверху
вниз, слева
направо.
Обход
выбранного
дерева
вывода
выполняется
процедурой
вычислителя
атрибутов,
на вход
которой
поступают
корень
дерева
выражения
и аксиома
грамматики.
Процедура
использует
правило A  z0X1z1...Xkzk,
связанное
с указанной
вершиной n,
и заданный
нетерминал
A, чтобы
определить
соответствующие
им вершины n1, ..., nk
и нетерминалы
X1, ..., Xk. Затем
вычислитель
рекурсивно
обходит
каждую
вершину
ni, имея на
входе
нетерминал
Xi.
z0X1z1...Xkzk,
связанное
с указанной
вершиной n,
и заданный
нетерминал
A, чтобы
определить
соответствующие
им вершины n1, ..., nk
и нетерминалы
X1, ..., Xk. Затем
вычислитель
рекурсивно
обходит
каждую
вершину
ni, имея на
входе
нетерминал
Xi.
9.9.4 Атрибутная
схема для
алгоритма
сопоставления
образцов
Алгоритмы 9.1
и 9.2 являются
«универсальными»
в том
смысле, что
конкретные
грамматики
выражений
и образцов
являются,
по-существу,
параметрами
этих
алгоритмов.
В то же
время, для
каждой
конкретной
грамматики
можно
написать
свой
алгоритм
поиска
образцов.
Например,
в случае
нашей
грамматики
выражений и
приведенных
на рис. 9.16
образцов
алгоритм 9.2
может быть
представлен
атрибутной
грамматикой,
приведенной
ниже.
Наследуемый
атрибут Match
содержит
упорядоченный
список
(вектор)
образцов
для
сопоставления
в поддереве
данной
вершины.
Каждый из
образцов
имеет вид
либо <op op-list> (op -
операция
в данной
вершине, а op-list
- список ее
операндов),
либо
представляет
собой
нетерминал
N. В первом
случае op-list
«распределяется»
по потомкам
вершины для
дальнейшего
сопоставления.
Во втором
случае
сопоставление
считается
успешным,
если есть
правило
N  op {Pati}, где w
состоит из
образцов,
успешно
сопоставленных
потомкам
данной
вершины.
В этом
случае по
потомкам в
качестве
образцов
распределяются
элементы
правой
части
правила.
Эти два
множества
образцов
могут
пересекаться.
Синтезируемый
атрибут Pattern
- вектор
логических
значений,
дает
результат
сопоставления
по вектору-образцу
Match.
op {Pati}, где w
состоит из
образцов,
успешно
сопоставленных
потомкам
данной
вершины.
В этом
случае по
потомкам в
качестве
образцов
распределяются
элементы
правой
части
правила.
Эти два
множества
образцов
могут
пересекаться.
Синтезируемый
атрибут Pattern
- вектор
логических
значений,
дает
результат
сопоставления
по вектору-образцу
Match.
Таким
образом, при
сопоставлении
образцов
могут
встретиться
два случая:
- Вектор образцов
содержит
образец
<op {Pati}>, где op - операция,
примененная
в данной
вершине.
Тогда распределяем
образцы
Pati по потомкам
и сопоставление
по данному
образцу
считаем
успешным
(истинным),
если успешны
сопоставления
элементов
этого образца
по всем потомкам.
- Образцом
является
нетерминал
N. Тогда рассматриваем
все правила
вида N
 op {Pati}. Вновь
распределяем
образцы
Pati по потомкам
и сопоставление
считаем
успешным
(истинным),
если успешны
сопоставления
по всем потомкам.
В общем случае
успешным
может быть
сопоставление
по нескольким
образцам.
op {Pati}. Вновь
распределяем
образцы
Pati по потомкам
и сопоставление
считаем
успешным
(истинным),
если успешны
сопоставления
по всем потомкам.
В общем случае
успешным
может быть
сопоставление
по нескольким
образцам.
Отметим,
что в общем
случае в
потомки
одновременно
передается
несколько
образцов
для
сопоставления.
В приведенной
ниже
атрибутной
схеме не
рассматриваются
правила
выбора
покрытия
наименьшей
стоимости
(см. предыдущий
раздел).
Выбор
оптимального
покрытия
может быть
сделан
еще одним
проходом
по дереву,
аналогично
тому, как
это было
сделано
выше.
Например,
в правиле
с '+' имеется
несколько
образцов
для Reg, но
реального
выбора
одного
из них не
осуществляется.
Кроме
того, не
уточнены
некоторые
детали
реализации.
В частности,
конкретный
способ
формирования
векторов Match
и Pattern. В тексте
употребляется
термин
«добавить»,
что
означает
добавление
к вектору
образцов
очередного
элемента.
Векторы
образцов
записаны
в угловых
скобках.
RULE
Stat ::= '=' Reg Reg
SEMANTICS
Match<2>=<'+' Reg Const>;
Match<3>=;
Pattern<0>[1]=Pattern<2>[1]&Pattern<3>[1].
|
Этому
правилу
соответствует
один
образец 2.
Поэтому в
качестве
образцов
потомков
через их
атрибуты Match
передаются,
соответственно,
<'+' Reg Const> и .
RULE
Reg ::= '+' Reg Reg
SEMANTICS
if (Match<0> содержит Reg в позиции i)
{Match<2>=;
Match<3>=>;
}
if (Match<0> содержит образец <'+' Reg Const> в позиции j)
{добавить Reg к Match<2> в некоторой позиции k;
добавить Const к Match<3> в некоторой позиции k;
}
if (Match<0> содержит образец <'+' Reg Const> в позиции j)
Pattern<0>[j]=Pattern<2>[k]&Pattern<3>[k];
if (Match[0] содержит Reg в i-й позиции)
Pattern<0>[i]=(Pattern<2>[1]&Pattern<3>[1])
|(Pattern<2>[2]&Pattern<3>[2])
|(Pattern<2>[3]&Pattern<3>[3]).
|
Образцы,
соответствующие
этому
правилу,
следующие:
(4) Reg  '+' Reg Const,
'+' Reg Const,
(5) Reg  '+' Reg Reg,
'+' Reg Reg,
(6) Reg  '+' Reg '@' '+' Reg Const.
'+' Reg '@' '+' Reg Const.
Атрибутам
Match второго и
третьего
символов в
качестве
образцов
при
сопоставлении
могут быть
переданы
векторы
Reg, Reg> и Reg, <'@' '+' Reg Const>>,
соответственно.
Из анализа
других
правил
можно
заключить,
что при
сопоставлении
образцов
предков
левой
части
данного
правила
атрибуту
Match символа
левой
части
может быть
передан
образец <'+' Reg Const>
(из образцов
2, 3, 6) или
образец
Reg.
RULE
Reg ::= '@' Reg
SEMANTICS
if (Match<0> содержит Reg в i-й позиции)
Match<2>=<<'+' Reg Const>,Reg>;
if (Match<0> содержит <'@' '+' Reg Const> в j-й позиции)
добавить к Match<2> <'+' Reg Const> в k позиции;
if (Match<0> содержит Reg в i-й позиции)
Pattern<0>[i]=Pattern<2>[1]|Pattern<2>[2];
if (Match<0> содержит <'@' '+' Reg Const> в j-й позиции)
Pattern<0>[j]=Pattern<2>[k].
|
Образцы,
соответствующие
этому
правилу,
следующие:
(3) Reg  '@' '+' Reg Const,
'@' '+' Reg Const,
(7) Reg  '@' Reg.
'@' Reg.
Соответственно,
атрибуту
Match второго
символа в
качестве
образцов
при
сопоставлении
могут быть
переданы
<'+' Reg Const> (образец
3) или
(образец 7).
Из анализа
других
правил
можно
заключить,
что при
сопоставлении
образцов
предков
левой
части
данного
правила
атрибуту Match
могут быть
переданы
образцы <'@' '+' Reg Const>
(из образца
6) и Reg.
RULE
Reg ::= Const
SEMANTICS
if (Pattern<0> содержит Const в j-й позиции)
Pattern<0>[j]=true;
if (Pattern<0> содержит Reg в i-й позиции)
Pattern<0>[i]=true.
|
Для дерева
рис. 9.15 получим
значения
атрибутов,
приведенные
на рис. 9.19.
Здесь M
обозначает
Match, P - Pattern, C - Const, R - Reg.
Назад Оглавление Вперёд