Введение
Хорошо известна следующая задача. Имеется
N городов
T[0] .. T[N-1]. Расстояние между каждой парой
T[i],
T[j] определяется длиной соединяющего их отрезка
где А – матрица расстояний между городами. Необходимо указать кратчайший маршрут, который начинается городом T[0], проходит через города T[1] .. T[n-2] и заканчивается городом T[N-1].
В теоретическом плане задача решается легко: достаточно перебрать все перестановки городов T[1] .. T[n-2] на маршруте и выбрать ту из них, которая доставляет кратчайший путь. Однако этот метод при существующих возможностях ПК дает результат за приемлемое время вычислений (от нескольких секунд до минуты), если N<10. С дальнейшим увеличением N быстродействие комбинаторного метода быстро снижается и его нельзя использовать в практических расчетах.
Среди других методов решения подобных практических задач (к ним, в частности, можно отнести близкую к рассматриваемой задачу коммивояжера) обычно используют единственный альтернативный метод ветвей и границ (МВГ). Считается, что он обеспечивает точное решение за минимальное время вычислений. Метод, действительно, хорошо работает на "учебных" примерах, однако, как показали эксперименты с МВГ на практических (логистических) примерах решения рассматриваемой задачи, его быстродействие сильно зависит от вида матрицы А и в большинстве случаев МВГ не гарантирует результативности в приемлемое время даже при N=15.
При всей известности задачи не удалось ни в научной литературе, ни в Интернет найти быстрых методов, которые позволили бы приближенно решить задачу с достаточной для практики точностью до 10% за приемлемое время.
Ниже рассмотрено несколько сравнительно быстрых приближенных эвристических методов решения задачи, которые удовлетворяют упомянутому условию. Методы реализуют процессы поиска базового маршрута и последующего его улучшения. При их описании использованы терминология теории графов и средства языка Object Pascal среды Delphi.
1 Методы нахождения базового маршрута
Метод 1.1 («жадный»,
Greedily). Сначала на графе, образованном матрицей
А, отыскивается и включается в маршрут вершина (город)
T[k] , которая ближе всех к начальной. Далее отыскивается самая близкая к
T[k] из числа еще не включенных в маршрут и т. д. В результате получается приближенное решение задачи – базовый маршрут.
Метод 1.2 («деревянный», Woody). Сначала в маршрут включаются две вершины начальная T[0] и конечная T[N-1]. Далее отыскивается вершина, которая характеризуется наименьшим расстоянием D(T[i]+T[k]) + D(T[k]+T[j]) — D(T[i] + T[j]), где i = 0, j = N-1, k – номера еще не включенных в маршрут вершин. Найденная вершина помещается в маршрут (0, k, N-1). На следующем шаге отыскивается вершина L, которая характеризуется наименьшим расстоянием DL от звена (0, k), и вершина M, имеющая наименьшее расстояние DM от звена (k, N-1). Среди L и M выбирается та, которая имеет наименьшее из DL и DM, и включается внутрь своего звена (0, k) или (k, N-1). Пусть это вершина M с номером m. Теперь маршрут состоит из трех звеньев (0, k), (k, m), (m, N-1). Процесс продолжается до тех пор, пока есть не включенные в маршрут вершины.
Метод 1.3 (простейший, Simply). Промежуточные вершины в маршрут включаются случайным образом. В частности, базовым будет допустимый маршрут G[i] = i.
Маршруты, построенные этими методами, вычисляются с очень высокой скоростью (практически мгновенно). Однако длина этих маршрутов в подавляющем большинстве случаев далека от практически приемлемой. Для этих целей применено несколько методов улучшения базового маршрута.
2 Методы улучшения базового маршрута
Метод 2.1 (перестановок,
Permutations). Совершается последовательный проход по парам соседних вершин всех звеньев с перестановкой этих вершин. Если перестановка уменьшает длину маршрута, то этот маршрут считается текущим. Производятся новые попытки улучшить его тем же методом до тех пор, пока перестановки не дадут эффекта. Далее аналогичным образом выполняются перестановки по трем соседним вершинам из числа тех, которые не попали в число ранее проведенных операций с двумя соседними вершинами (перестановки более широкого диапазона, т. е. по 4 и более, не выполнялись). Эксперименты с графами показали, что процедура улучшения маршрута при помощи перестановок достаточно эффективна и быстродействие ее весьма высоко.
Метод 2.2 (удаление петлей, CrossDeleting). Часто текущий маршрут содержит петли. Например, на рисунке 1 цепочка вершин 5-7-3-8-2-4 образуют петлю. Петля начинается с левой по ходу маршрута вершины отрезка 5-7 и заканчивается правой вершиной отрезка 2-4. Существование петли определяется наличием пересекающихся отрезков маршрута. Если внутреннюю цепочку петли повернуть в противоположном направлении, то есть заменить указанную цепочку на 5-2-8-3-7-4, то петля исчезнет (рисунок 2), а маршрут станет короче. Метод отличается чрезвычайно высоким быстродействием и высокой эффективностью.
|
|
|
Рисунок 1. Маршрут с петлей |
|
Рисунок 2. Улучшенный маршрут |
Метод 2.3 (разворот цепочек, ChainTurnings). Как показали эксперименты, отсутствие петлей еще не означает, что процедура разворота цепочек без петлей неэффективна. Для оптимизации текущего маршрута применялась процедура разворота всех возможных цепочек. Метод имеет самое низкое быстродействие в сравнении с другими методами улучшения. Поэтому на практике его применяли для цепочек с числом звеньев не более шести.
Метод 2.4 (комбинированный, CorrectPath). После нахождения какого-нибудь базового маршрута G к нему применялась комбинированная процедура улучшения по методам 2.1 – 2.3. Хотя метод 2.2 является частным случаем метода 2.3, его все равно применяли из-за высокого быстродействия и способности к эффективному разворота цепочек из любого числа звеньев. Метод имеет код:
procedure CorrectPath(N: Integer; var G: TIntVec; var Path: Integer);
begin
repeat
until not Permutations(N,G) and not ChainTurnings(N,G) and
not CrossDeleting(N,G) and not MoveTops(N,G);
Path:= PathByG(N,G); // расчет длины маршрута
end;
3 Приближенные комбинированные методы нахождения кратчайшего маршрута
Применив три метода
1.1,
1.2,
1.3 расчета базового маршрута и комбинированный метод
2.4 их улучшения, получили три приближенных метода расчета маршрута:
метод 3.1:
procedure GreedilyCorrect(N: Integer; var G: TIntVec; var Path: Integer);
begin
Greedily(N,G);
CorrectPath(N,G,Path);
end;
метод 3.2:
procedure WoodyCorrect(N: Integer; var G: TIntVec; var Path: Integer);
begin
Woody(N,G);
CorrectPath(N,G,Path);
end;
и метод 3.3:
procedure SimplyCorrect(N: Integer; var G: TIntVec; var Path: Integer);
begin
Simply(N,G);
CorrectPath(N,G,Path);
end;
В экспериментах с методами 3.1–3.3 установлено, что ни один из них не является предпочтительным. В зависимости от матрицы А лучший результат с равной вероятностью мог дать любой из этих методов (интересно, что даже простейший базовый маршрут G[i] = i после улучшений нередко трансформировался в самый короткий маршрут, что свидетельствует о том, что решение задачи практически не зависит от выбора базового маршрута). Поэтому в качестве рабочего применяли комбинированный метод 3.4 (комбинация всех), суть которого состоит в последовательном применении методов 3.1–3.3 к матрице А с последующим выбором лучшего маршрута среди сформированных этими методами.
Для того чтобы можно было оценить точность приближенной методики разработана рекурсивная процедура (RecoursiveMethod), позволяющая получить точное решение задачи переборным методом. Для повышения быстродействия в процедуру внесены некоторые очевидные эвристические усовершенствования. Процедура позволила получить точное решение за приемлемое для проведения необходимых оценок время (до 5 минут на вариант размещения городов) при N<23.
Для оценки точности метода 3.4 при больших значениях N (N>22) процедуру RecoursiveMethod применить нельзя, поэтому составлена процедура Rand многократного применения метода 3.3 к одной и той же матрице А с различными случайными базовыми маршрутами. Процедура последовательно формирует маршруты до тех пор, пока последний лучший маршрут не повторится 5 раз подряд. Нельзя сказать, что такой способ позволяет найти самый короткий маршрут. Однако результаты работы процедуры дают интуитивную уверенность в том, что сравнение «быстрого» результата с результатом длительной работы метода 3.4 имеет достаточно высокую вероятность корректности за неимением точных методов. Уверенность в этом подкреплена весьма важным выводом, который получен после обработки сотен различных матриц для N<23. Он состоит в полном совпадении результатов, полученных с использованием точной процедуры RecoursiveMethod и приближенной Rand (т. е. для данных N процедура Rand всегда находила точное решение задачи).
Скриншот интерфейса разработанной в среде Delphi 6 программы показан на рисунке 3.
Рисунок 3. Интерфейс программы
В качестве примера на рисунке представлен кратчайший маршрут из вершины 0 в вершину 13 (N = 14) для матрицы расстояний, которая показана на рисунке 4.
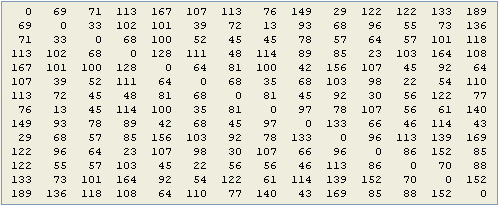
Рисунок 4. Матрица расстояний
На рисунках 5-10 показаны результаты расчета маршрутов и их протяженности (Комб и Rand) для случайного расположения городов при помощи быстрой процедуры комбинированного метода 3.4 и процедуры Rand. В последней колонке таблиц приведена процентная погрешность метода 3.4, которую рассчитывали по формуле 100 (Комб-Rand)/Комб, %.
|
|
|
|
|
Рисунок 5 |
|
Рисунок 6 |
|
Рисунок 7 |
|
|
|
|
|
Рисунок 8 |
|
Рисунок 9 |
|
Рисунок 10 |
В результате экспериментов с несколькими сотнями матриц расстояний для различных N, получены данные, которые свидетельствуют, что независимо от количества N городов погрешность метода 3.4 никогда не превосходила 8% при N<101. Средняя погрешность составила 2%, что вполне приемлемо для практики.
На основании обработки многочисленных расчетных данных получена формула ориентировочной оценки быстродействия метода 3.4. Среднее время t (с) расчета на компьютере с процессором Intel 1400 кратчайшего маршрута с N городами составило
Так, для N = 100 среднее время расчета маршрута составляет 4 секунды. Для практически используемых N<31 это время не превосходит 0,1 с.
К материалу прилагаются файлы: