Предисловие переводчика
С моей точки зрения, оптимизация запросов является наиболее важным и интересным направлением исследований и разработок во всей области баз данных. Важность этого направления определяется тем, что от развитости компонента оптимизации запросов критически зависит общая производительность любой SQL-ориентированной СУБД (я ограничиваюсь этим классом систем, потому что, во-первых, они полностью довлеют на современном рынке СУБД, и, во-вторых, методы оптимизации наиболее развиты именно для SQL-запросов). Я считаю это направление наиболее интересным, потому что при решении задач оптимизации приходится использовать самые разнообразные подходы и методы из различных областей вычислительной науки и математики: методы оптимизации программ, применяемые в компиляторах языков программирования, математическую логику, математическую статистику, методы искусственного интеллекта, распознавания образов и т.д.
На протяжении последних тридцати лет эти факторы привлекают к данному направлению внимание сотен исследователей, опубликовавших тысячи статей, многие из которых доступны и/или интересны только профессионалам. Но некоторое знакомство с методами оптимизации запросов полезно гораздо более широкой аудитории: проектировщикам и администраторам систем баз данных, разработчикам приложений баз данных и даже пользователям этих приложений. Такое знакомство обеспечивают обзоры методов оптимизации. До сих пор русскоязычным читателям были доступны моя обзорная статья и перевод более современной обзорной статьи Сураджита Чаудхари.
Мне кажется, что для полноты картины очень полезно познакомится с еще более ранней статьей Ярке и Коха, перевод которой мы и предлагаем вашему вниманию. Перечитывая эту статью, я обнаружил в ней достоинства, которыми, к сожалению, не обладают более поздние обзоры: последовательность и систематичность. Авторы пытаются (и преуспевают в этом) представить последовательную картину процесса оптимизации запроса. В свое время меня раздражало то, что они ведут свое изложение не прямо в контексте языка SQL, а используют более абстрактное представление запросов на языке реляционного исчисления. Однако сейчас мне понятно, что этот подход позволил авторам отвлечься от не слишком существенных технических трудностей оптимизации, специфичных для языка SQL, и сосредоточиться на более фундаментальных методах оптимизации.
Для справедливости следует заметить, что в 1984 г. было гораздо проще написать фундаментальный обзор методов оптимизации, чем в настоящее время. За прошедшие 20 лет было разработано множество методов, существенной части которых нельзя отказать в фудаментальности. Поэтому в наше время очень трудно выбрать стиль изложения, позволяющий описать текущее состояние данного направления исследований в такой же последовательной и логичной манере, что я Ярке и Коха. Тем более рекомендую прочитать русский вариант этой замечательной статьи, которая лично на меня оказала очень серьезное влияние.
Содержание
Эффективные методы обработки непредвиденных запросов являются решающей предпосылкой успеха обобщенных систем управления базами данных. Предлагалось множество подходов к совершенствованию
эффективности алгоритмов вычисления запросов: основанные на логике и семантические преобразования, быстрые реализации основных операций, комбинаторные и эвристические алгоритмы генерации возможных
путей доступа и выбора между ними.
Эти методы представляются в каркасе общей процедуры вычисления запроса использованием для представления запросов реляционного исчисления. Кроме того, затрагиваются аспекты нестандартной
оптимизации запросов, такие как вычисление запросов более высокого уровня, оптимизация запросов в распределенных базах данных и использование машин баз данных. Однако основное внимание уделяется
оптимизации запросов в централизованных системах баз данных.
ВВЕДЕНИЕ
Системы управления базами данных (СУБД) стали стандартным инструментом экранирования пользователя компьютера от деталей управления вторичной памятью. СУБД разрабатываются для повышения
производительности труда прикладных программистов и облегчения доступа к данным неискушенных в комьютерах конечных пользователей.
Имеются две основные области исследований систем баз данных. Одна из них - это анализ моделей данных, на которые может отображаться реальный мир и на основе которых могут строиться интерейсы для
различных типов пользователей. Такие концептуальные модели включают иерерхическую, сетевую, реляционную модели, а также ряд моделей, ориентированных на семантику, которые обозревались в большом числе
книг и обзоров [Brodie et al. 1984].
Вторая область интересов затрагивает безопасную и эффективную реализацию СУБД. Комьютеризоаванные данные становятся центральным ресурсом большинства организаций. Это должно учитываться в каждой
реализации, предназначенной для производственного использования, путем гаранирования безопасности данных в случаях параллельного доступа [Bernstein and Goodman 1981c], восстановления [Verhofstad
1978] и реорганизации [Sockut and Goldberg 1979]. Одно из основных критических замечаний ко многим ранним СУБД относилось к отсутствию эффективности при обработке предлагаемых ими мощных операций, в
особенности, доступа к данным на основе их содержимого через запросы. Оптимизация запросов предназначена для решения этой проблемы путем интеграции большого числа методов и стратегий,
простирающихся от логических преобразований запросов до оптимизации путей доступа и хранения данных на уровне файловых систем.
Традиционно в каждом из этих подходов использовался отдельный язык. Вероятно, это является одной из причин, по которым до сих пор не представлен исчерпывающий обзор методов оптимизации запросов.
Целью этой статьи является представление методов оптимизации запросов в общем каркасе реляционного исчисления. Показано, что реляционной исчисление технически эквивалентно представлению реляционной
алгебры [Codd 1972; Klug 1982a] и поддается расширениям для реализации сетевых СУБД [Dayal and Goodman 1982]. Более того, многие популярные языки запросов, такие как SQL [Astrahan and Chamberlin
1975] и QUEL [Stonebraker et al. 1976], легко отображаются в реляционное исчисление.
Для экономии места в этой статье мы прежде всего сосредотачиваемся на проблеме оптимизации запросов в централизованной СУБД. Оптимизация централизованных запросов важна не только во многих базах
данных на мейнфреймах - а в последнее время и в микропроцессорных СУБД - но также является подпроблемой оптимизации запросов в распределенных системах. Сама оптимизация распределенных запросов [Bayer
et al. 1984; Sacco and Yao 1982; Ullman 1982] затрагивается только кратко, а следующих двух близких областей мы вообще не касаемся:
Пользовательская оптимизация. Общая стоимость информационной системы составляется из стоимости СУБД и стоимости усилий пользователей для работы с системой. Граница между этими двумя
областями состоит из функциональных возможностей и удобства использования языка запросов [Vassiliou and Jarke 1984], и наиболее важной характеристикой является время отклика системы. Если
предположить, язык запросов обладает заданными функциональными возможностями, а минимизация времени отклика является целью системы выполнения запросов, то оптимизация запросов может считаться
отдельно трактуемой подпроблемой пользовательской оптимизации.
Структуры файлов. Алгоритм оптимизации запросов должен производить выбор между множеством путей доступа для выполнения запроса. Внутренние детали реализации таких путей доступа и вывод
соответствующих оценочных форму (см., например, Teorey and Fry [1982]) находятся за пределами этой статьи.
Статья состоит из шести разделов, расположенных в соответствии с подходом "сверху-вниз". В разд. 1 мы представляем глобальный каркас для оптимизации запросов. В разд. 2 мы сравниваем четыре метода
представления запросов с точки зрения их пригодности для оптимизации. В разд. 3 мы используем один из этих методов, реляционное исчисление, для представления преобразований, основанных на логике,
включая развивающиеся методы семантической оптимизации.
После преобразования запрос должен быть отображен в последовательность операций, возвращающих требуемые данные. В разд. 4 мы анализируем реализацию таких операций в низкоуровневой системе хранения
данных и путей доступа. В разд. 5 мы представляем оптимизационные процедуры для интеграции этих операций в глобально оптимальный план доступа.
Для ряда проблем оптимизации запросов требуется трактовка по причине более высокой сложности запросов или некоторых характеристик используемой апаратуры. Обзор трех таких проблемных областей -
запросы более высокого уровня, распределенные запросы и запросы с использованием машин баз данных - приводится в разд. 6.
1. ПРОБЛЕМА ОПТИМИЗАЦИИ ЗАПРОСОВ
Точная оптимизация процедур вычисления запросов является, вообще говоря, вычислительно трудной, и еще больше мешает отсутствие точной статистической информации о базе данных. В алгоритмах
вычисления запросов приходится в большой степени полагаться на эвристики. Тем не менее, в статье будет использоваться термин "оптимизация запросов" для обозначения стратегий, направленных на
повышение эффективности процедур вычисления запросов. В этом разделе мы формулируем цели оптимизации запросов и представляем общую процедуру, разработанную для структуризации процесса поиска
решения.
1.1 Запросы
Запрос - это языковое выражение, которое описывающее данные, подлежащие выборке из базы данных. В конетексте оптимизации запросов часто предполагается, что запросы выражаются в манере, основанной
на содержании, (в большинстве случаев ориентированной на множества, что дает оптимизатору достаточную возможность выбора между возможными процедурами вычисления.
Запросы используются в нескольких окружениях. Наиболее очевидно приложение, в котором поступают непосредственные запросы конечного пользователя, нуждающегося в информации о структуре или
содержимом базы данных. Если потребности пользователей ограничены набором стандартных запросов, они могут оптимизироваться вручную путем программирования соответствующих процедур поиска и ограничения
пользовательского ввода форматом меню. Однако, если требуется задавать непредвиденные запросы с использованием языка запросов общего назначения, становится необходимой система автоматической
оптимизации запросов.
Второе применение запросов происходит в транзакциях, которые изменяют хранимые данные на основе их текущих значений (например, "повысить зарплату всем доцентам на 10%"). Наконец, выражения,
подобные запросам, могут использоваться внутри СУБД, например, для проверки прав доступа [Griffiths and Wade 1976], поддержки ограничений целостности [Stonebraker 1975] и корректной синхронизации
параллельного доступа [Reimer 1983].
1.2 Цели оптимизации
Экономический принцип требует, чтобы процедуры оптимизации пытались либо максимизировать пропускную способность при заданном числе ресурсов, либо минимизоровать потребление ресурсов при данной
пропускной способности. Оптимизация запросов направленая на минимизация времени отклика для заданного запроса и смеси типов запросов в данной системной среде. Эта общая цель допускает ряд различных
операционных целевых функций. Время отклика является разумной целью только при предположении, что время пользователя является наиболее важным критическим ресурсом. В противном случае можно стремиться
к непосредственной минимизации стоимости потребления технических ресурсов. К счастью, обе цели являются в большой степени взаимнодополнительными; при возникающие конфликты целей обычно разрешаются
путем назначения ограничений на доступные технические ресурсы (например, на размер буферного пространства в основной памяти).
Чтобы допустить справедливое сравнение эффективности, функциональные возможности сравниваемых систем выполнения запросов должны быть сходными. Требование "реляционной полноты", придуманное Коддом
[Codd 1972], (сравните с разд. 2.1) стало квазистандартом. Методы, обозреваемые в данной статье, представляются как вклады в реализацию запросов на реляционно полном языке с минимальной стоимостью
выполнения или временем отклика. Запросы более высокого уровня сложности [Chandra and Harel 1982a] рассматриваются в разд. 6.1. Общая стоимость, подлежащая минимизации, складывается из следующих
компонентов:
Стоимость коммуникаций: Стоимость передачи данных из места, в котором они хранятся, в места, где выполняются вычисления и представляются результаты. Эта стоимость состоит из стоимости
коммуникационного канала, которая обычно связана с временем, в течение которого канал открыт, и стоимостью задержек в обработке, вызваемых передачей. Последний компонент, более важный для оптимизации
запросов, часто полагается линейной функцией от объема передаваемых данных.
Стоимость доступа к вторичной памяти: Стоимость (или время) загрузки страниц данных из вторичной памяти в основную память. На эту стоимость влияет выбираемых данных (главным образом, размер
промежуточных результатов), кластеризация данных на физических страницах, размер доступного буферного пространства и скорость используемых устройств.
Стоимость хранения: Стоимость занятия вторичной памяти и буферов основной памяти. Стоимость хранения уместна только в том случае, когда память становится узким местом системы, и размер
требуемой памяти может изменяться от запроса к запросу.
Стоимость вычислений: Стоимость (или время) использования ЦП.
На структуру алгоритмов оптимизации запросов влияют соотношения между этими компонентами стоимости. В территориально распределенной СУБД с относительно медленными коммуникационными каналами преобладает
стоимость коммуникацонных задержек, а другие факторы существенны только для локальной подоптимизации. В централизованных системах доминирует время доступа к вторичной памяти, хотя для сложных
запросов достаточно высокой может быть и стоимость ЦП [Gotlieb 1975]. В локально распределенных СУБД все факторы имеют близкие веса, что приводит к очень сложным оценочным функциям и процедурам
оптимизации.
Поскольку эта статья в основном посвящена централизованным базам данных, стоимость коммуникаций не принимается во внимание, потому что в таких системах комуникационные требования не зависят от
стратегии выполнения запросов. Для оптимизации одиночных запросов стоимость хранения также считается не первостепенно важной. Эти расходы учитываются только при одновременной оптмизации нескольких
запросов.
Остаются стоимость доступа ко вторичной памяти (обычно измеряемая числом обращения к страницам) и стоимость использования ЦП (часто измеряемая числом сравнений, которые требуется произвести). В
основе большинства методов, разработанных для сокращения этой стоимости, лежит ряд общих идей: (1) избегать дублирования усилий; (2) использовать стандартизованные компоненты; (3) заглядывать вперед,
чтобы избегать лишних операций; (4) выбирать наиболее дешевые способы выполнения элементарных операций; (5) выстраивать их последовательность оптимальным образом. Следующий простой пример показывает,
что можно ожидать от оптимизации запросов.
Рассмотрим реляционную схему базы данных, описывающей служащих, предлагающих компьютерные лекции отделам географически распределенной организации:
employees (enr, ename, status, city)
papers (enr, title, year)
departments (dname, city, street address)
courses (cnr, cname, abstract)
lectures (cnr, dname, enr, daytime)
Ключевые атрибуты подчеркнуты; заданная комбинация значений ключевых атрибутов уникально идентифицирует элемент отношения. Предположим, что пользователя интересуют "названия отделов, расположенных
в Нью-Йорке и предлагающих курсы по управлению базами данных".
Имеется много возможных стратегий разрешения этого запроса, три из которых сравниваются по отношению к следующим предположениям относительно реальных значений данных. Заметим, что детальные
данные, используемые в приводимых ниже вычислениях, обычно недоступны оптимизатору запросов, а должны оцениваться.
Имеется 100 отделов, 5 из которых размещаются в Нью-Йорке. В физическом блоке может поместиться 5 записей об отделах или 50 значений dname.
Имеется 500 курсов, 20 из которых посвящены управлению базами данных. В физическом блоке помещается 10 записей.
Имеется 2000 лекций, три сотни из них - про управление базами данных, 100 проходят в отделах в Нью-Йорке и 20 (из трех отделов) удовлетворяют обоим условиям. В физический блок помещаются 10
записей.
Предположим также, что время сортировки составляет N * log(2)N, где N - размер файла в блоках, и что имеется буфер из одного блока для каждого отношения. Наконец, все отношения
физически упорядочены по возрастанию значений ключа.
Первая представленная здесь стратегия следует прямому подходу трансляции выражения реляционного исчисления в операции алгебры [Codd 1972]. Вместе с каждым шагом стратегии приводится число
обращений ко вторичной памяти, требующихся для чтения (r) и записи (w).
Стратегия 1
- Сформировать декартово произведение отношений "courses", "lectures" и "departments"
(r: 200000)
- Оставить столбец dname из тех записей "departments", для которых значения столбцов cnr в "courses" и "lectures" совпадают, и значения столбцов dname из "lectures" и "departments" совпадают, и
cname = 'database management' and city = 'New York'.
(w: 1)
итого: приблизительно 200000 обращений.
Исключительно высокая стоимость этой стратегии происходит из того факта, что она генерирует промежуточный результат, очень небольшая часть которого действительно существенна для дальнейшей
обработки. Эффективность может быть существенно повышена путем рассмотрения только тех комбинаций элементов разных отношений, которые имеют одинаковые значения общих атрибутов. Путем использования
существующих порядков сортировки, такие комбинации могут формироваться "слиянием" участвующих отношений. Эта операция называется "соединением".
Стратегия 2
- Выполнить слияние отношений "courses" и "lectures"
(r: 50 + 200; w: 400)
- Отсортировать результат по dnames
(r + w: 400*1og(2)400)
- Выполнить слияние результата с отношением "departments"
(r: 400 + 20; w: 400 + 400)
- Выбрать комбинации с cname = 'database management' and city = 'New York'
(r: 800)
- Оставить только столбец dname.
(w: 1)
Итого: Приблизительно 6000 обращений.
Стоимость ответа на запрос можно еще более сократить путем выполнения ограничений на основе значений как можно раньше и уменьшения за счет этого расходов на сортировку и слияние промежуточных
результатов.
Стратегия 3
- Выполнить слияние отношений "courses" и "lectures"
(r: 50 + 200)
- Оставить только dnames из комбинаций cname = 'database management'
(w: 2)
- Отсортировать сгенерированный список dname
(r + w: 2)
- Выполнить слияние результата с отношением "departments"
(r: 2 + 20)
- Оставить только те dnames, для которых city = 'New York'
(w: 1)
Итого: 277 обращений
Таким образом, было достигнуто сокращение стоимости приблизительно в 700 раз. Для больших баз данных и более сложных запросов более совершенные методы могут привести к еще большим сокращениям.
1.3 Нисходящий подход к оптимизации запросов
Исследования оптимизации запросов, представленные в литературе, можно разбить на два класса, которые можно охарактеризовать как восходящий и низходящий. Исследователи находят общую проблему
оптимизации запросов очень сложной. Теоретические работы начались с восходящего подхода, изучения особых случаев, таких как оптимальная реализация важных операций и стратегии вычисления для некоторых
простых подклассов запросов. В дальнейшем исследователи пытались собрать их этих начальных результатов более крупные строительные блоки.
Потребность в работающих системах инициировала разработку полномасштабных процедур вычисления запросов, что повлияло на общность решений и заставило заниматься оптимизацией запросов в
единообразной и эвристической манере [Astrahan and Chamberlin 1975; Makinouchi et al. 1981; Niebuhr et al. 1976; Palermo 1972; Schenk and Pinkert 1977; Wong and Youssefi 1976]. Поскольку часто это не
позволяло достичь конкурентноспособной эффектвности систем, современной тенденцией представляется нисходящий подход, который обеспечивает возможность включения в общие процедуры большего знания о
возможностях оптимизации в частных случаях. В то же время, сами общие алгоритмы усиливаются комбинаторными процедурами минимизации стоимости для выбора между стратегиями.
В этой статье мы придерживаемся нисходящего подхода, применяя общую процедуру вычисления, служащую каркасом для конкретных методов, разработанных при исследовании оптимизации запросов:
Шаг 1. Найти внутреннее представление запросов, в которое могут легко отображаться запросы пользователей, оставляющее системе все необходимые степени свободы для оптимизации выполнения
запросов.
Шаг 2. Применить логические преобразования к представлению запроса, которые (1) стандартизируют запрос, (2) упрощают запрос, чтобы избежать дублирования усилий, (3) улучшают запрос для
упрощения его выполнения и создания возможности применения процедур частных случаев.
Шаг 3. Отобразить преобразованный запросв в возможную последовательность элементарных операций, для которых известна хорошая реализация и соответсвующие оценки стоимости. В результате этого
шага появляется набор возможных "планов доступа".
Шаг 4. Вычислить общую стоимость каждого плана доступа, выбрать наиболее дешевый план и выполнить его.
Первые два шага этой процедуры являются в большой степени независимыми и поэтому часто могут быть выполнены во время компиляции. Качество шагов 3 и 4, т.е. изобилие генерируемых планов доступа и
оптимальность алгоритма выбора сильно зависит от знания значений в базе данных.
Последствия от зависимости от данных являются двоякими. Во-первых, если база данных изменчива, то шаги 3 и 4 могут быть выполнены только во время выполнения. Это означает, что возможный выигрыш в
эффективности должен соотноситься со стоимостью самой оптимизации. Во-вторых, в метабазе данных (например, расширяемом справочнике данных) должна поддерживаться общая нформация о структуре базе
данных, равно как и статистическая информация о содержимом базы данных. Как и во многих схожих операционных исследовательских проблемах (например, в управлении запасами) стоимость получения и
поддержки этой добавочной информации должна сопоставляться с ее качеством.
2. ПРЕДСТАВЛЕНИЕ ЗАПРОСОВ
Запросы могут представляться в ряде форм. В контексте оптимизации запросов уместное представление запросов должно удовлетворять следующим требованиям: Оно должно быть достаточно мощным для
выражения большого класса запросов и должно обеспечивать правильно построенный базис для преобразования запросов. В этом разделе мы представляем четыре разные формы представления запросов, каждая из
которых используется в ряде походов к оптимизации запросов.
2.1 Реляционное исчисление
(Кортежное) реляционное исчисление, как оно было введено Коддом [Codd 1971, 1972], - это нотация для определения результата запроса через описание его свойств. Представление запроса в реляционном
исчислении состоит из двух частей: целевой список (target list) и выражение выборки (selection expression).
Выражение выборки специфицирует содержимое отношения, происходящего в результате выполнения запроса, средствами предикатов первого порядка (т.е. обобщенных булевских выражений, возможно,
содержащих кванторы существования и всеобщности). В целевом списке определяются свободные переменные, встречающиеся в предикате, и специфицируется структура результирующего отношения. В
Примере 2.1 демонстрируется представление реляционного исчисления с использованием синтаксиса языка программирования баз данных Pascal/R [Schmidt 1977].
Пример 2.1. Имена профессоров, опубликовавших какую-либо статью в 1981 г.
[<e.ename> OF
EACH e IN employees:
e.status = professor
AND
SOME p IN papers
(e.enr = p.enr AND p.year = 1981)]
В целевом списке, т.е. подвыражении, предшествующем двоеточию, область определения (свободной) переменной e ограничивается элементами отношения "employees". Поэтому отношение "employees"
называется отношением области определения (range relation) переменной e. Спецификация атрибута цели "<e.ename>" показывает, что в результате запроса останутся только имена служащих.
Выражение выборки - предикат, следующий за двоеточием - определяет ограничения на свободную переменную. Первое ограничение является ограничивающим, или одноместным термом (monadic term),
ограничивающим свободную переменную теми записями "employees", значением столбца status которых является значение "professor". Это ограничение связывается через AND с соединительным, или
двуместным термом (dyadic term), связывающим "employees" с "papers", и еще одним одноместным термом, еще более ограничивающим результат теми служащими, которые опубликовали какую-либо статью в
1981 г. Обычно допускаемыми в термах операциями сравнения являются =, `, <, >, d и e.
В отличие от односортового исчисления предикатов, в реляционном исчислении разрешаются переменные, привязанные к разным сортам (отношениям области определения); например, переменная e связана с
"employees", а переменная p - с "papers". Последствия многосортовости реляционного исчисления в отношение преобразования запрсов обсуждаются в разд. 3.1.
Кроме логической операции AND, в предикатах могут использоваться и операции OR и NOT. Предикаты реляционного исчисления полностью определяются следующими рекурсивными правилами:
- Атомарные предикаты:
- (Одноместный или двуместный) терм является атомарным предикатом.
- TRUE является атомарным предикатом.
- FALSE является атомарным предикатом.
- Атомарный предикат является предикатом. Пусть A - предикат, r - переменная элемента, и rel - отношение. Тогда
- SOME r IN rel(A),
- ALL r IN rel(A)
также являются предикатами.
- Пусть A и B - предикаты. Тогда
- NOT (A) (отрицание),
- A AND B (конъюнкция),
- A OR B (дизъюнкция)
являются предикатами.
- Никакие другие формулы предикатами не являются.
Реляционное исчисление было введено в [Codd 1972] как мерило реляционной мощности. Форма представления называется реляционно полной, если в ней допускается определение результата любого
запроса, определяемого выражением реляционного исчисления. Ясно, что реляционная полнота должна рассматриваться как минимальное требование в отношении выразительной мощности. Часто приводимым
примером концептуально простого запроса, выходящим за пределы реляционной полноты, является запрос "найти имена служащих, отчитывающихся перед менеджером Смитом на любом уровне", предусматривающий,
что в одном отношении моделируется иерархия служащий (через атрибуты name и manager) [Pirotte 1979]. Кроме того, запросы в сегодняшних приложениях часто содержат агрегации, которые неаозможно
выразить в чистом реляционном исчислении. Однако реляционное исчисление довольно легко расширяется агрегатными функциями [Klug 1982b; Maier and Warren 1981].
2.2 Реляционная алгебра
Реляционная алгебра, как она определена Коддом в [Codd 1972] является набором операций над отношениями. Эти операции распадаются на два класса: традиционные операции над множествами, такие как
декартово произведение, объединение, пересечение и разность, и специальные операции реляционной алгебры, такие как ограничение, проецирование, соединение и деление. Ниже специальные операции
определяются путем их связывания с эквивалентными выражениями реляционного исчисления.
Операция ограничения, примененная к отношению "rel", конструирует горизонтальное подмножество в соответствии с безкванторным предикатом, содержащим только одноместные термы или
"внутриотношенческие" двуместные термы (сравнения между атрибутами одного элемента отошения):
Rest(rel, pred) = [EACH r IN rel: pred].
Операция проекции служит для конструирования вертикального подмножества отношения "rel" путем выбора набора указанных атрибутов A и удаления кортежей-дубликатов из этих атрибутов:
Proj(rel, A) = [(r.A) OF EACH r IN rel: true].
Операция соединения позволяет соединять два отношения "rel1" и "rel2" в одно отношение, атрибуты которого являются объединением атрибутов "rel1" и
"rel2":
Join(rel1, A op B, rel2) =
[EACH rl IN rel1, EACH r2 IN rel2: rl.A op r2.B].
Допускаемые в соединениях операции сравнения "op" являются такими же, как в двуместных термах реляционного исчисления. Если "op" является операцией сравнения на равенство, в результате
"естественного" соединения опускается A или B.
Операция деления является алгебраическим двойником квантора всеобщности. Она определяется следующим образом:
Divi(rel1, A by B, rel2) =
[(r.compl(A)) OF EACH rl IN rel1:
ALL rel2 IN rel2 SOME r3 IN rel1
(rl.compl(A) = rel2.compl(A) AND rel2.B = r3.A)],
где compl(A) - это дополнение A во множестве атрибутов "rel1". Как показывает определение, деление является довольно сложной операцией, что может затруднить понимание запросов.
В Примере 2.2 представляется запрос Примера 2.1 в терминах реляционной алгебры.
Пример 2.2. Имена профессоров, опубликовавших какую-либо статью в 1981 г.
Proj (Rest(Join(employees,
enr = enr,
Rest(papers, year = 1981)),
status = professor),
ename)
В противоположность выражению реляционного исчисления, которое описывает отношение, проиходящее из запроса, в терминах его свойств, выражение релционной алебры определяет алгоритм конструирования
результирующего отношения. Выражение исчисления кажется лучшей стартовой точкой для оптимизации запросов, поскольку оно обеспечивает оптимизатор только базовыми свойствами запроса; возможности
оптимизации могут быть скрыты в конкретной последовательности операций алгебры. Однако в отношении реляционной полноты реляционная алгебра, по меньшей мере, настолько же полна, как и реляционное
исчисление. В [Codd 1972] показано, что любое выражение реляционного исчисления можно отрранслировать в эквивалентное выражение алгебры. Аналогичный результат для выражений алгебры и исчисления,
расширенных агрегатыми функциями доказан Клугом [Klug 1982a].
2.3 Графы запросов
Графы используются для визуального представления структурированных объектов в ряде областей. Двумя хорошо известными примерами являются использование синтаксических деревьев при конструировании
компиляторов и использование графов AND/OR в приложениях искусственного интеллекта. При оптимизации запросов графы используются для представления запросов и стратегий вычисления запросов. Можно
выделить два класса графов: объектные графы и графы операций.
В объектных графах узлы представляют объекы, такие как переменные (отношений) и константы. Дуги описывают предикаты, которым эти объекты должны удовлетворять [Bernstein and Chiu 1981;
Palermo 1972; Youssefi and Wong 1979]. Объектные графы содержат свойства результатов запросов и поэтому тесно связаны с реляционным исчислением. Графы операций описывают управляемые операциями
потоки данных путем представления операций как узлов, связанных дугами, указывающими направление движения данных. В [Smith and Chang [1975]; Yao [1979] графы операций использовались для представления
выражений алгебры. На рис. 1 и рис. 2 приведены примеры объектного графа и графа операций соответственно.
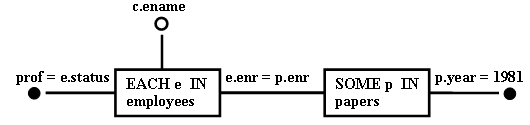
Рис. 1. Объектный граф, представляющий запрос из примера
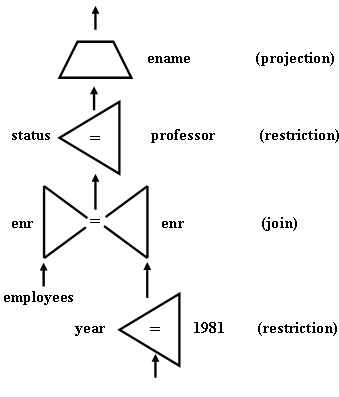
Рис. 2. Граф операций, представляющий запрос из примера
У графов запросов имеется много привлекательных свойств. Визуальное представление запроса способствует более простому пониманию его структурных характеристик. Кроме того, в теории графов имеется
много результатов, полезных для автоматического анализа графов, например, обнаружение циклов и свойства древовидности. Наконец, важным достоинством графов запросов является то, что их легко расширять
дополнительной информацией. Например, расширение графов деталями физической организации данных предложено в [Rosenthal and Reiner 1982].
2.4 Табло
Табло, как они были определены Ахо и др. [Aho et al. 1979a, 1979b, 1979c] являются табличной нотацией для подмножества запросов реляционного исчисления, характеризующихся наличием только связанных
через AND термов и отсутствием кванторов всеобщности. Таким образом табло-запросы представляют собой частный вид
конъюнктивных запросов [Chandra and Merlin 1977; Rosenkrantz and Hunt 1980].
Табло представлют собой специализированные матрицы, столбцы которых соответствуют атрибутам соответствующей схемы базы данных. Первая строка матрицы, сводка (summary), служит тем же целям, что
целевой список выражения реляционного исчисления. Остальные строки описывают предикат. Символы, появляющиеся в табло, являются выделенными (distinguished) переменными (соответствующими свободным
переменным), невыделенными (nondistinguished) переменными (соответствующими переменным под знаком квантора существования), константами, пробелами и тэгами (указывающими отношения областей
определения).
На рис. 3 иллюстрируется конструирование табло, представляющего запрос из Примера 2.1. Процесс начинается с табло для одиночных отношений и продолжается путем комбинирования этих табло в новые
табло для все больших выражений. Выделенные переменные отмечаются символами a; невыделенные - символом b.
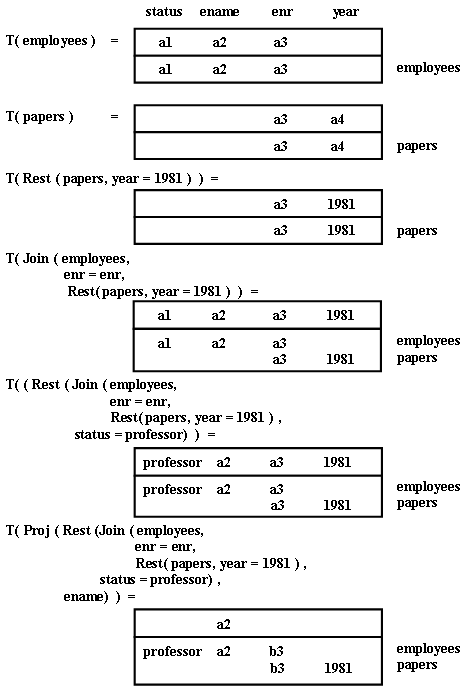
Рис. 3. Пошаговое конструирование табло T, представляющего запрос из Примера 2.1
Выражения, содержащие дизъюнкцию (объединение множеств) и отрицание (вычитание множеств) могут представляться наборами табло [Sagiv and Yannakakis 1980]. В [Klug 1983] и Johnson and Klug 1983]
набора табло используются для представления общих конъюгктивных запросов. Конкретная значимость табло в отношении оптимизации запросов обсуждается в разд. 3.2.
3. ПРЕОБРАЗОВАНИЕ ЗАПРОСОВ
Мы видим, что запросы могут выражаться в ряде различных форм. Кроме того, даже внутри заданного языка для каждого запроса можетсуществовать ряд семантически эквивалентных выражения. Предметом этого
раздела являются преобразование выражения запросов в эквивалентное выражение на основе правильно определенных правил. Цели преобразования запросов являются троякими: (1) конструирование
стандартизованной стартовой точки для оптимизации запроса (
стандартизация), (2) устранение избыточности (
упрощение) и (3) консруирование усовершенствованных выражений по отношению к
эффективности выполнения (
улучшение - amelioration).
3.1 Стандартизация
В нескольких подходах к оптимизации запросов стандартизованная стартовая точка определяется через нормализованный вариант используемой формы представления запроса [Jarke and Schmidt 1981; Kim 1982;
Palermo 1972; Wong and Youssefi 1976]. Здесь мы представляем две нормальные формы для реляционного исчисления, а также правила, которым должна подчиняться процедура нормализации.
Говорят, что представление запроса с использованием реляционного исчисления находится в предваренной нормальной форме (prenex normal form), если его выражение выборки имеет вид
SOME/ALL rel1 IN rel1 . . .
SOME/ALL rn IN reln(M),
где M - предикат, не содержащий кванторов. M называется матрицей (matrix) и тоже может быть стандартизован. Говорят, что матрица, состоящая из дизъюнкции конъюнкций (термов
Aij), такая как
(A11 AND . . . AND A1n) OR . . .
OR (Am1 AND . . . AND Amn),
находится в дизъюнктивной нормальной форме, а матрица, состоящая из конъюнкции дизъюнктов, такая как
(A11 OR . . . OR A1n) AND . . .
AND (Am1 OR . . . OR Amn),
находится в конъюнктивной нормальной форме
Предваренная нормальная форма с нормальными формами матрицы приводит к двум нормальным формам выражений реляционного исчисления: дизъюнктивной предваренной нормальной форме (disjunctive prenex
normal form, DPNF) и конъюнктивной предваренной нормальной форме (conjunctive prenex normal form, СPNF). Использование DPNF мотивируется целью раздельной оптимизации и выполнения
независимых компонентов запросов [Bernstein et al. 1981]. CPNF оказалась полезной для декомпозиции запросов [Wong and Youssefi 1976] и для зависящего от данных улучшения запроса (например, проверка в
первую очередь наиболее ограничительного дизъюнта).
Запросы в CPNF могут подвергаться дальнейшему преобразованию к не содержащей кванторов форме, популярной в приложениях доказательства теорем искусственного интеллекта, к так называемой
клаузальной форме (clausal form) [Nilsson 1982]. Языки баз данных, основанные на логике, такие как Prolog [Kowalski 1981], основываются на клаузальной форме. Поскольку клаузальная форма редко
используется при оптимизации запросов (в качестве исключений см. Grant and Minker [1981], Jarke et al. [1984] и Warren [1981]) здесь мы опускаем подробности.
Преобразование произвольного выражения реляционного исчисления к предваренной нормальной форме состоит в перемещении кванторов по термам (справа налево). Перемещение кванторов управляется
правилами преобразований, представленными в таб. 1. Нормализация матрицы может достигаться с применением правил ДеМоргана, правил дистрибутивности и правила двойного отрицания (см. таб. 2).

Таб. 1. Правила преобразований для выражений с кванторами

Таб. 2. Правила преобразований для общих выражений
Различия для случаев пустых и непустых отношений областей определения в правилах Q2 и Q3 таб. 1 возникают из-за изменчивости отношений во времени и многосортности реляционного исчисления [Jarke
and Schmidt 1982]. Выражение реляционного исчисления может быть преобразовано к односортному исчислению путем введения области определения, такой как (r IN rel), как еще одного типа атомарного
предиката:
O1: SOME r IN rel(pred)
<=> SOME r((r IN rel) AND pred),
O2: ALL r IN rel(pred)
<=> ALL r((r IN rel) Т pred).
Применение правил Q2a и Q3a при перемещение квантора из терма вызвало бы поэтому неверный результат в случае пустого отношения области определения. Из этого следует, что при нормализации
произвольного выражения реляционного исчисления во время компиляции необходимо сохранять информацию об исходных определениях областей определения переменных, чтобы при необходимости во время
выполнения можно было произвести модификации в соответствии с правилами Q2b и Q3b.
3.2 Упрощение
Мы уже видели, что может существовать несколько семантически эквивалентных выражений одного и того же запроса. Одним из источников различия между двумя эквивалентными выражениями являеься из уровень
избыточности [Hall 1976; Stroet and Engmann 1979]. Прямолинейное вычисление избыточного выражения привело бы к выполнению набора операций, некоторые из которых являются излишними. Поэтому оптимизатор
запросов стремится к устранению избыточности путем преобразованию избыточного выражения к эквивалентному выражению, не являющемуся избыточным.
Избыточное выражение выражение может быть упрощено путем применения правил преобразования M4a-M4j, в которых учитывется идемпотентность (см. таб. 2). Применение этих правил усложняется тем
фактом, что идемпотентность может встретиться на любом уровне выражения по причине наличия общих подвыражений, т.е. подвыражений, которые могут встретиться более одного раза в выражении,
представляющем запрос. Поэтому, чтобы упростить, например, выражение
[EACH e IN employees:
e.ename = 'Smith'
OR
(e.status = assistant
OR e.status = professor)
AND
NOT(e.status = professor
OR e.status = assistant)]
до
[EACH e IN employees: e.ename = 'Smith']
посредством правил M4d и M4g, сначала нужно распознать эквивалентность подвыражений
(e.status = assistant OR e.status = professor)
и
(e.status = professor OR e.status = assistant)
Алгоритмы приводятся в [Downey et al. 1980 и Hall 1974, 1976]. Распознавание общих подвыражений и применение правил идемпотентности должно выполняться скорее совместно, чем последовательно,
поскольку при упрощении выражения на основе правил идемпотентности могут появиться новые общие подвыражения, которые, в свою очередь, являются предметом упрощения. Выражения, связанные с пустыми
отношениями, также можно упрощать. Правила преобразований для их упрощения приводятся в таб. 3. (Заметим, что эти правила можно применять только во время выполнения.)
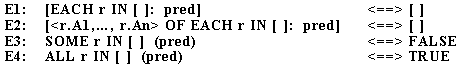
Таб. 3. Правила преобразований для выражений с пустыми отношениями
Термы, как они определены в разд. 2.1, в реляционном исчислении служат атомарными предикатами. Однако эти термы могут быть упрощены или удалены, если явно учитывается семантика операций сравнения.
Важным приложением является так называемое распространение констант, в котором используются законы транзитивности, такие как
r.A op s.B AND s.B = const
=> r.A op const,
позволяющее сократить в запросе число двуместных термов. В алгоритмах минимизации числа строк в табло (см. разд. 2.4) систематически используются такие правила упрощения для конъюнктивных запросов
[Aho et al. 1979a; Sagiv 1981, 1983]. Поскольку число строк в табло больше числа соединений (двуместных соединительных термов) в выражении, минимизация числа строк соответствует исключению избыточных
соединений.
Сагив и Яннакакис [Sagiv and Yannakakis 1980] расширяют методы табло для обеспечения возможности упрощения выражений, содержащих дизъюнкты. Однако обобщение методов для всех выражений реляционно
полного языка все еще остается открытой проблемой.
Для "семантического" упрощения запросов может использоваться информация о семантических ограничениях целостности [Aho et al. 1979a, 1979b, 1979c; Jarke et al. 1984; Johnson and Klug 1982; Ott and
Horlaender 1982; Rosenthal and Reiner 1984]. В качестве простого примера рассмотрим случай ограничений ключа. Если r и r' - это (свободные или связанные квантором существования)
переменные с одной и той же область определения, отношением "rel", то эквисоединение вида "r.key = r'.key" является избыточным в том смысле, что этот терм и одна из переменных, например,
r' могут быть удалены с подстановкой r вместо r' в любом терме, в который входит r'. Этот тип упрощения особенно пригоден в контексте обработки представлений, когда
преобразование пользовательских запросов над представлениями к системным запросам над хранимыми отношениями может привнести существенную избыточность. Область применения семантического упрощения
может быть расширена за счет привлечения дополнительных ограничений, порождаемых структурой запроса [Klug 1980; Koch et al. 1981].
Заключительная возможность упрощения возникает в тех случаях, когда удается показать, что один или несколько конъюнктов матрицы стандартизованного запроса никогда не удовлетворяются [Eswaran et
al. 1976; Klug 1983; Munz et al. 1979; Ozsoyoglu and Yu 1980]. Для примера рассмотрим выражение
r.A ≥ s.B AND s.B > t.C AND t.C ≤ r.A,
которое порождает противоречие r.a > r.a и поэтому может быть заменено булевским значением false. Проблема определения невыполнимости условия терма эффективно решается во время
компиляции для конъюнкции термов с операциями сравнения (=, <, &le , >, &ge) [Rosenkrantz and Hunt 1980], но вычислительно сложна, если допускается операция сравнения на неравенство.
3.3 Улучшение
В результате упрощения запроса не обязательно производится уникальное выражение. Могут существовать другие неизбыточные выражения, семантически эквивалентные тому, которое сгенерировано некоторым
методом упрощения. Вычисление выражений, соответствующих одному и тому же запросу может существенно различаться параметрами эффективности, например, размерами промежуточных результатов и числом
обращений к элементам отношений. Ниже приводится ряд эвристик для таких преобразований запросов, выполнение которых улучшает выражения в отношении эффективности их вычисления.
Простейшими преобазованиями, рассматриваемыми в этом разделе, являются объединение последовательности проекций в одну проекцию и объединение последовательности ограничений в одно
ограничение [Hall 1976; Smith and Chang 1975]. Соответствующими правилами преобразования являются следующие:
A1: Proj(. . . Proj(Proj(rel, A1), A2), . . . , An)
==> Proj(rel, An),
A2: Rest(. . . (Rest(Rest(rel, predl), pred2) . . . , predn)
==> Rest(rel, predl AND pred2 AND . . . AND predn).
Объединение внутриотношенческих операций обеспечивает два преимущества. Во-первых, избегается повторяющееся чтение одного и того же отношения, и, во-вторых, существующие пути доступа могут
использоваться для объединенной операции, а не только для первой операции последовательности.
Целью ряда улучшающих преобразований является минимизация размера конструируемых, сохраняемых и считываемых промежуточных результатов. Важная эвристика перемещает селективные операции, такие как
ограничение и проекция, выше контруктивных операций, таких как соединение и декартово произведение, чтобы выполнять селективные операции как можно раньше [Smith and Chang 1975]. В контексте
реляционного исчисления разбор некоторой последовательности вычислений может быть представлен вложенным выражением. Вычисление вложенного выражения начинается с вычисления наиболее внутреннего
вложенного выражения, за которым следует непосредственно окружающее его выражение и т.д., пока не будет достигнуто наиболее внешнее выражение. Вложенное выражение, подразумевающее раннее вычисление
одноместных термов (ограничений) приведено в Примере 3.1.
Пример 3.1. Вложенное выражение, эквивалентное выражению из Примера 2.1.
[<e.ename) OF
EACH e IN [EACH e IN employees:
e.status = professor]:
SOME p IN [EACH p IN papers:
p.year = 1981]
(e.enr = p.enr)]
Ранее вычисление селективных операций представляет частный случай отсоединения запроса (query detachment), введенного Вонгом и Юссефи [Wong and Youssefi 1976]. Подвыражение, которое
перекрывается с оставшейся частью запроса по одной переменной, отсоединяется и образует внутреннюю вложенность. Отсоединение выполняется рекурсивно на каждом уровне вложенности до тех пор, пока
выражение не перестанет сокращаться. Эксперименты, описанные Юссефи и Вонгом [Wong and Youssefi 1979], показали, что это очень сильная эвристика. В Примере 3.2 демонстрируется отсоединение
подвыражения сложного выражения.
Пример 3.2. Отделы, предлагающие лекции, проводимые профессорами, которые живут в том же городе, в котором находится отдел, и каждый из которых опубликовал
какую-либо статью в 1981 г.
Соответствующее выражение:
[EACH d IN departments:
SOME l IN lectures
SOME e IN employees
(e.status = professor
AND
d.dname = l.dname
AND 1.enr = e.enr
AND e.city = d.city
AND
SOME p IN papers
(p.year = 1981
AND p.enr = e.enr))]
Вот эквивалентное выражение, произведенное путем отсоединения запроса:
[EACH d IN departments:
SOME l IN lectures
SOME e IN [EACH e IN
[EACH e IN employees:
e.status = professor]:
SOME p IN [EACH p IN
papers: p.year = 1981]
(e.enr = p.enr)]
(d.dname = 1.dname AND 1.enr = e.enr
AND e.city = d.city)]
Объектный граф, представляющий запрос, показан на рис. 4.
Заметим, что результирующее вложенное выражение является неразделимым [Goodman and Shmueli 1980]; т.е. его нельзя разделить на два подвыражения, перекрывающихся по одной переменной. Другими
словами, вложенное выражение содержит цикл (см. рис. 4).
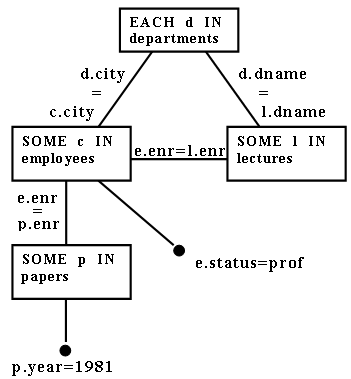
Рис 4. Объектный граф для Примера 3.2
Важность различения циклических и ациклических (древовидных) выражения для обработки запросов подробнее обсуждается в разд. 4.3. Пока мы лишь заметим, что бывают циклы, которые можно преобразовать
к эквивалентным ациклическим графам. В число таких циклов входят те, которые (1) вводятся по транзитивности [Bernstein and Chiu 1981; Yu and Ozsoyoglu 1979], (2) содержат некоторые комбинации дуг,
соотвествующих соединительным термам с условием сравнения на неравенство [Bernstein and Goodman 1981b; Ozsoyoglu and Yu 1980], (3) являются "замкнутыми" посредством переменных, связанных квантором
всеобщности [Jarke and Koch 1983] и (4) содержат переменные, которые можно подвергнуть декомпозиции с использованием функциональных зависимостей [Kambayashi and Yoshikawa 1983].
Понятия расширенных выражений областей определения (extended range expressions) [Jarke and Schmidt 1982] и вложенных областей определения (range nesting) [Jarke and Koch 1983]
обеспечивают обобщение отсоединения запросов, поскольку в них учитываются выражения с кванторами всеобщности. Отношения базы данных, задающие область определения кортежной переменной замещаются
выражениями исчисления в соответствии со следующими правилами преобразований:
A3: [EACH r IN rel: predl AND pred2]
<=> [EACH r IN [EACH r IN rel: predl]: pred2],
A4: SOME r IN rel(predl AND pred2)
<=> SOME r IN [EACH r IN rel: predl] (pred2),
A5: ALL r IN rel: (NOT(predl) OR (pred2)
<=> ALL r IN [EACH r IN rel: predl] (pred2).
Заметим, что особенно полезно правило преобразования A5 для переменных, связанных квантором всеобщности, поскольку при сокращении числа конъюнктов на внешнем уровне вложенности можно ожидать
существенного уменьшения размеров промежуточных результатов.
В представленных до сих пор улучшающих преобразованиях используется информация из трех источников: общие правила преобразования и эвристики, управляющие их применением, знание сруктур реляционных
данных и сам запрос. Пока не рассмотрены два других источника знаний: ограничения целостности, которые во многих базах данных дополняют структурное определение схемы и реальные данных в базе
данных.
Ограничения целостности - это предикаты, которые должны быть истинными для каждого элемента некоторого отношения или каждой комбинации элементов некоторой группы отношений. Поэтому их можно
добавлять к выражению выборки любого запроса без изменения его истинностного значения. Имеется несколько подходов, в которых это наблюдение используется скорее для улучшения, а не для упрощения
(последняя возможность упоминалась в предыдущем разделе). Они называются основанной на знаниях (knowledge-based) [Hammer and Zdonik 1980] или семантической обработкой запросов [King 1979,
1981].
Предположим, например, что ограничение целостости говорит: "Мы принимаем на работу только профессоров, которые публикуют, по крайней мере, одну статью в год". В этом случае вычисление запроса из
Примера 2.1 (в котором спрашиваются имена профессоров со статьями в 1981 г.) становится тривиальным, а вычисление запроса из Примера 3.2 существенно упрощается.
Добавление ограничения целостности к выражению выборки может также изменить структуру запроса, делая его более приспособленным для обработки. Нассмотрим ограничение: "Мы принимаем на работу только
местных профессоров". В этом случае терм "d.city = e.city" в примере 3.2 можно опустить. В объектном графе оставшегося запроса больше не содержится цикл.
Успех семантической обработки запросов сильно зависит от разработки эффективных эвристик для выбора между многими преобразованиями, делающими возможным добавление к запросу любой комбинации
ограничений целостности. В [King 1981] и [Xu 1983] для принятия этого решения для специального класса реляционных баз данных используются правила в духе искусственного интеллекта.
Яо [Yao 1979] указывает, что существуют случаи, в которых оптимальное преобразование является зависимым от данных. Представленные выше эвристики могут быть не всегда оптимальными, особенно
в тех случаях, когда некоторые пути доступа поддерживаются структурами физического хранения. Одним из последствий такой зависимости от данных является то, что средства преобразования запросов должны
поддерживаться не только во время компиляции, но и во время выполнения. Кроме того, если эвристики не приносят удовлетворительных результатов, требуется одновременная оптимизация на физическом и
логическом уровнях. Однако, прежде чем обратиться к таким интегрированным подходам, необходимо описать физическое выполнение компонентов запросов.