2008 г.

Базы данных. Вводный курс

Сергей Кузнецов

7.2.3. Минимальное покрытие множества функциональных зависимостей

Множество FD S2 называется покрытием множества FD S1, если любая FD, выводимая из S1, выводится также из S2.

Легко заметить, что S2 является покрытием S1 тогда и только тогда, когда S1⁺S2⁺. Два множества FD S1 и S2 называются эквивалентными, если каждое из них является покрытием другого, т. е. S1⁺ = S2⁺.

Множество FD S называется минимальным в том и только в том случае, когда удовлетворяет следующим свойствам:

правая часть любой FD из S является множеством из одного атрибута (простым атрибутом);
детерминант каждой FD из S обладает свойством минимальности; это означает, что удаление любого атрибута из детерминанта приводит к изменению замыкания S⁺, т. е. порождению множества FD, не эквивалентного S³⁰⁾;
удаление любой FD из S приводит к изменению S⁺, т. е. порождению множества FD, не эквивалентного S.

Чтобы продемонстрировать минимальные и неминимальные множества FD, вернемся к примеру отношения СЛУЖАЩИЕ_ПРОЕКТЫ {СЛУ_НОМ, СЛУ_ИМЯ, СЛУ_ЗАРП, ПРО_НОМ, ПРОЕКТ_РУК} с рис. 7.1. Если считать, что единственным возможным ключом этого отношения является атрибут СЛУ_НОМ, то множество FD {СЛУ_НОМСЛУ_ИМЯ, СЛУ_НОМСЛУ_ЗАРП, СЛУ_НОМПРО_НОМ, ПРО_НОМПРОЕКТ_РУК} будет минимальным. Действительно, в правых частях FD этого множества находятся множества, состоящие ровно из одного атрибута; каждый из детерминантов тоже является множеством из одного атрибута, удаление которого, очевидно, недопустимо; удаление каждой FD явно приводит к изменению замыкания множества FD, поскольку утрачиваемая информация не выводится с помощью аксиом Армстронга.

С другой стороны, множества FD

{СЛУ_НОМ{СЛУ_ИМЯ, СЛУ_ЗАРП}, СЛУ_НОМПРО_НОМ, СЛУ_НОМПРОЕКТ_РУК, ПРО_НОМПРОЕКТ_РУК},
{СЛУ_НОМСЛУ_ИМЯ, {СЛУ_НОМ, СЛУ_ИМЯ}СЛУ_ЗАРП, СЛУ_НОМПРО_НОМ, СЛУ_НОМПРОЕКТ_РУК, ПРО_НОМПРОЕКТ_РУК} и
{СЛУ_НОМСЛУ_НОМ, СЛУ_НОМСЛУ_ИМЯ, СЛУ_НОМСЛУ_ЗАРП, СЛУ_НОМПРО_НОМ, СЛУ_НОМПРОЕКТ_РУК, ПРО_НОМПРОЕКТ_РУК}

не являются минимальными. Для множества (1) в правой части первой FD присутствует множество из двух элементов. Для множества (2) удаление атрибута СЛУ_ИМЯ из детерминанта второй FD не меняет замыкание множества FD. Для множества (3) удаление первой FD не приводит к изменению замыкания. Эти примеры показывают, что для определения минимальности множества FD не всегда требуется явное построение замыкания данного множества.

Интересным и важным является тот факт, что для любого множества FD S существует (и даже может быть построено) эквивалентное ему минимальное множество S^-.

Приведем общую схему построения S^- по заданному множеству FD S. Во-первых, используя правило (5) (декомпозиции), мы можем привести множество S к эквивалентному множеству FD S1, правые части FD которого содержат только одноэлементные множества (простые атрибуты). Далее, для каждой FD из S1, детерминант D {D₁, D₂, …, D_n} которой содержит более одного атрибута, будем пытаться удалять атрибуты D_i, получая множество FD S2. Если после удаления атрибута D_i S2 эквивалентно S1, то этот атрибут удаляется, и пробуется следующий атрибут. Назовем S3 множество FD, полученное путем допустимого удаления атрибутов из всех детерминантов FD множества S1. Наконец, для каждой FD f из множества S3 будем проверять эквивалентность множеств S3 и S3 MINUS {f}. Если эти множества эквивалентны, удалим f из множества S3, и в заключение получим множество S4, которое минимально и эквивалентно исходному множеству FD S.

Пусть, например, имеется отношение R {A, B, C, D} и задано множество FD S = {AB, ABC, ABC, ACD, BC}. По правилу декомпозиции S эквивалентно множеству S1 {AB, AC, ABC, ACD, BC}. В детерминанте FD ACD можно удалить атрибут C, поскольку по правилу дополнения из FD AC следует AAC; по правилу транзитивности выводится FD AD, поэтому атрибут C в детерминанте FD ACD является избыточным. FD ABC может быть удалена, поскольку может быть выведена из FD AC (по правилу пополнения из этой FD выводится ABBC, а по правилу декомпозиции далее выводится ABC). Наконец, FD AC тоже выводится по правилу транзитивности из FD AB и BC. Таким образом, мы получаем множество зависимостей {AB, AD, BC}, которое является минимальным и эквивалентно S по построению.

Минимальным покрытием множества FD S называется любое минимальное множество FD S1, эквивалентное S.

Поскольку для каждого множества FD существует эквивалентное минимальное множество FD, у каждого множества FD имеется хотя бы одно минимальное покрытие, причем для его нахождения не обязательно находить замыкание исходного множества.

7.3. Декомпозиция без потерь и функциональные зависимости

Как уже отмечалось, в следующей лекции мы будем обсуждать подход к проектированию реляционных баз данных на основе нормализации, т. е. декомпозиции (разбиения путем проецирования) отношения, находящегося в предыдущей нормальной форме, на два или более отношений, удовлетворяющих требованиям следующей нормальной формы.

Считаются правильными такие декомпозиции отношения, которые обратимы, т. е. имеется возможность собрать исходное отношение из декомпозированных отношений без потери информации. Такие декомпозиции называются декомпозициями без потерь.

7.3.1. Корректные и некорректные декомпозиции отношений. Теорема Хита

На рис. 7.3 приведены две возможные декомпозиции отношения СЛУЖАЩИЕ_ПРОЕКТЫ (для экономии места мы сократили и слегка изменили тело отношения из рис. 7.1).

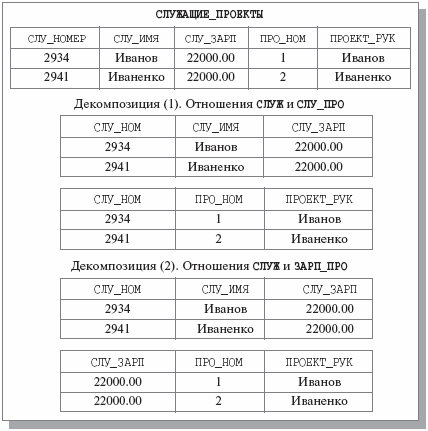
Рис. 7.3. Две возможные декомпозиции отношения СЛУЖАЩИЕ_ПРОЕКТЫ

Анализ рис. 7.3 показывает, что в случае декомпозиции (1) мы не потеряли информацию о служащих – про каждого из них можно узнать имя, размер зарплаты, номер выполняемого проекта и имя руководителя проекта. Вторая декомпозиция не дает возможности получить данные о проекте служащего, поскольку Иванов и Иваненко получают одинаковую зарплату, следовательно, эта декомпозиция приводит к потере информации. Что же привело к тому, что одна декомпозиция является декомпозицией без потерь, а вторая – нет?

Заметим, что при проведении декомпозиции мы использовали операцию взятия проекции. Каждое из отношений СЛУЖ, СЛУ_ПРО и ЗАРП_ПРО является проекцией исходного отношения СЛУЖАЩИЕ_ПРОЕКТЫ. В случае декомпозиции (1) отсутствие потери информации означает, что в результате естественного соединения отношений СЛУЖ и СЛУ_ПРО мы гарантированно получим отношение, заголовок и тело которого совпадают с заголовком и телом отношения СЛУЖАЩИЕ_ПРОЕКТЫ. Следует отметить, что это произойдет для любых допустимых (и согласованных) значений переменных отношений СЛУЖАЩИЕ_ПРОЕКТЫ, СЛУЖ и СЛУ_ПРО, поскольку у всех этих переменных атрибут СЛУ_НОМ является возможным ключом. Однако если выполнить естественное соединение отношений СЛУ и ЗАРП_ПРО, то будет получено отношение, показанное на рис. 7.4.

Схема этого отношения, естественно (поскольку соединение – естественное), совпадает со схемой отношения СЛУЖАЩИЕ_ПРОЕКТЫ, но в теле появились лишние кортежи, наличие которых и приводит к утрате исходной информации. Интуитивно понятно, что это происходит потому, что в отношении ЗАРП_ПРО отсутствуют функциональные зависимости СЛУ_ЗАРППРО_НОМ и СЛУ_ЗАРППРОЕКТ_РУК, но точнее причину потери информации в данном случае мы объясним несколько позже.

Корректность же декомпозиции 1 следует из теоремы Хита:

Теорема Хита.

Пусть задано отношение r {A, B, C} (A, B и C, в общем случае, являются составными атрибутами) и выполняется FD AB.

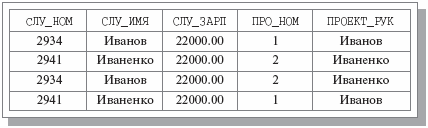
Рис. 7.4. Результат естественного соединения отношений СЛУЖ и ЗАРП_ПРО

Тогда r = (r PROJECT {A, B}) NATURAL JOIN (r PROJECT {A, C}).

Доказательство. Прежде всего, докажем, что в теле результата естественного соединения (обозначим этот результат через r₁) содержатся все кортежи тела отношения r. Действительно, пусть кортеж {a, b, c} r. Тогда по определению операции взятия проекции {a, b} (r PROJECT {A, B}) и {a, с} (r PROJECT {A, С}). Следовательно, {a, b, c} r₁. Теперь докажем, что в теле результата естественного соединения нет лишних кортежей, т. е. что если кортеж {a, b, c} r1, то {a, b, c} r. Если {a, b, c} r₁, то существуют {a, b} (r PROJECT {A, B}) и {a, с} (r PROJECT {A, С}). Последнее условие может выполняться в том и только в том случае, когда существует кортеж {a, b*, c} r. Но поскольку выполняется FD AB, то b = b* и, следовательно, {a, b, c} = {a, b*, c}. Конец доказательства.

Для иллюстрации общего случая применения теоремы Хита рассмотрим отношение СЛУЖАЩИЕ_ОТДЕЛЫ_ПРОЕКТЫ {СЛУ_НОМ, СЛУ_ОТД, ПРО_НОМ} (рис. 7.5). Атрибут СЛУ_ОТД содержит номера отделов, в которых работают служащие, а ПРО_НОМ – номера проектов, в которых служащие принимают участие. Каждый служащий работает только в одном отделе, т. е. имеется FD СЛУ_НОМСЛУ_ОТД, но один служащий может участвовать в нескольких проектах.

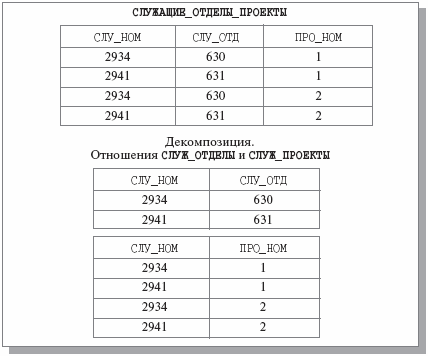
Рис. 7.5. Декомпозиция без потерь по теореме Хита

В отношении СЛУЖАЩИЕ_ОТДЕЛЫ_ПРОЕКТЫ атрибут СЛУ_НОМ не является возможным ключом, но, как показано на рис. 7.5, наличия FD СЛУ_НОМСЛУ_ОТД оказывается достаточно для декомпозиции этого отношения без потерь.

Для дальнейшего изложения нам потребуется ввести еще одно определение и сделать пару замечаний.

Атрибут B минимально зависит от атрибута A, если выполняется минимальная слева FD AB.

Например, в отношении СЛУЖАЩИЕ_ПРОЕКТЫ выполняются FD СЛУ_НОМСЛУ_ЗАРП и {СЛУ_НОМ, СЛУ_ИМЯ}СЛУ_ЗАРП. Первая FD является минимальной слева, а вторая – нет. Поэтому СЛУ_ЗАРП минимально зависит от СЛУ_НОМ, а для {СЛУ_НОМ, СЛУ_ИМЯ} свойство минимальной зависимости не выполняется.

7.3.2. Диаграммы функциональных зависимостей

Далее, для иллюстраций в следующей лекции нам пригодятся диаграммы FD, с помощью которых можно наглядно представлять минимальные множества FD. Например, на рис. 7.6 приведена диаграмма минимального множества FD отношения СЛУЖАЩИЕ_ПРОЕКТЫ.

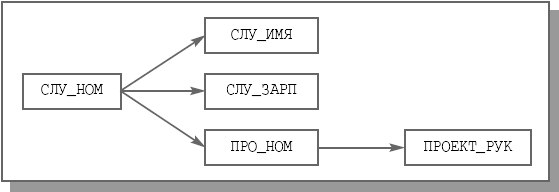
Рис. 7.6. Диаграмма минимального множества FD отношения СЛУЖАЩИЕ_ПРОЕКТЫ

В левой части диаграммы все стрелки начинаются с атрибута СЛУ_НОМ, который является единственным возможным (и, следовательно, первичным) ключом отношения СЛУЖАЩИЕ_ПРОЕКТЫ. Обратите внимание на отсутствие стрелки от СЛУ_НОМ к ПРОЕКТ_РУК. Конечно, поскольку СЛУ_НОМ является возможным ключом, должна выполняться и FD СЛУ_НОМПРОЕКТ_РУК. Но эта FD является транзитивной (через ПРО_НОМ) и поэтому не входит в минимальное множество FD. Заметим, что в процессе нормализации, к рассмотрению которого мы приступим в следующей лекции, из диаграмм множества FD удаляются стрелки, начинающиеся не от возможных ключей.

7.4. Заключение

В этой лекции было введено понятие функциональной зависимости и исследовались важные свойства функциональных зависимостей. Одна из целей состояла в том, чтобы на основе некоторого множества функциональных зависимостей суметь построить минимальное эквивалентное множество функциональных зависимостей. Мы начали обсуждение с понятия замыканий множества функциональных зависимостей и аксиом Амстронга, теоретически позволяющих построить такое замыкание. Замыкание множества функциональных зависимостей содержит все функциональные зависимости, выводимые из функциональных зависимостей заданного множества. Рассмотренный далее алгоритм построения замыкания множества атрибутов над заданным множеством функциональных зависимостей упрощает задачу, позволяя определить принадлежность заданной функциональной зависимости к замыканию заданного множества функциональных зависимостей без потребности в реальном построении замыкания.

Далее мы занялись покрытиями множеств функциональных зависимостей и минимальными множествами функциональных зависимостей. Наиболее важным результатом этой части лекции является доказательство существования и наметки алгоритма построения минимального покрытия заданного множества функциональных зависимостей – минимального множества функциональных зависимостей, эквивалентного исходному множеству.

Наконец, последний раздел лекции был посвящен критерию декомпозиции отношения без потерь, т. е. такому способу проецирования заданного отношения на два отношения, при котором результат естественного соединения проекций в точности совпадает с исходным отношением. Достаточное (и очень естественное) условие декомпозиции без потерь обеспечивает теорема Хита.

30 FD с минимальным детерминантом называется минимальной слева.

Назад Содержание Вперёд