2008 г.
Методы бикластеризации для анализа интернет-данных
Дмитрий Игнатов,
кафедра анализа данных и искусственного интеллекта ГУ-ВШЭ
Назад Содержание Вперёд
2.1.2. Формальный анализ понятий (ФАП)
Определение 2.11
Формальный контекст
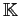
есть тройка
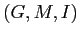
, где
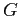
—
множество, называемое множеством
объектов,
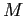
— множество,
называемое множеством
признаков,
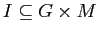
—
отношение.
Отношение 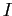 интерпретируется следующим образом: для
интерпретируется следующим образом: для 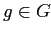 ,
, 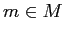 имеет место
имеет место 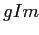 , если объект
, если объект 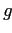 обладает признаком
обладает признаком 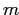 .
.
Для формального контекста
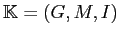 и произвольных
и произвольных
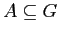 и
и
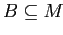 определена пара отображений:
определена пара отображений:
которые задают
соответствие Галуа между частично упорядоченными
множествами
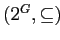
и
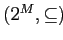
(см.
Раздел
2.1.1), а оператор
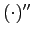
является
оператором замыкания на
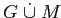
— дизъюнктном
объединении
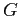
и
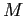
, т.е. для произвольного
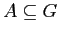
или
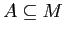
имеют место следующие
соотношения [
1]:
-
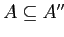 (экстенсивность),
(экстенсивность),
-
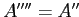 (идемпотентность),
(идемпотентность),
- если
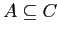 , то
, то
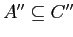 (изотонность).
(изотонность).
Множество 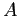 называется замкнутым, если
называется замкнутым, если
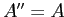 [1].
[1].
Определение 2.12
Формальное понятие формального контекста
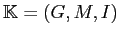
есть
пара
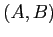
, где
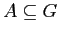
,
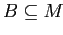
,
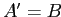
и
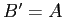
. Множество
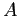
называется
объёмом, а
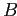
—
содержанием понятия
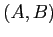
.
Очевидно, что объем и содержание произвольного формального понятия
являются замкнутыми множествами.
Множество формальных понятий контекста
 , которое мы будем
обозначать посредством
, которое мы будем
обозначать посредством
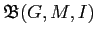 , частично упорядочено по вложению
объёмов: формальное понятие
, частично упорядочено по вложению
объёмов: формальное понятие
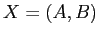 является менее общим
(более частным), чем понятие
является менее общим
(более частным), чем понятие
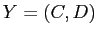 ,
,
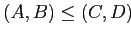 ,
если
,
если
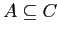 , что эквивалентно
, что эквивалентно
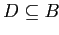 (
(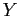 — обобщение
— обобщение 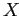 ).
).
В работе [1] было показано, что подмножества
произвольного множества, замкнутые относительно заданной на нем
операции замыкания, образуют полную решётку, а в работах
[83,33] — что множество
всех понятий формального контекста
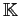 образует полную решётку.
образует полную решётку.
Определение 2.13
Множество понятий контекста
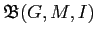
образует решётку
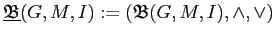
, где
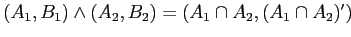
. и
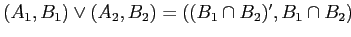
. Такие решётки
называют
решётками понятий, или
решётками
Галуа [
33].
Любая полная решётка изоморфна решётке понятий некоторого формального
контекста [33]. В качестве объектов этого контекста
нужно выбрать 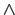 -неразложимые элементы, а в качестве признаков
—
-неразложимые элементы, а в качестве признаков
— 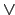 -неразложимые элементы исходной решётки. Тогда объект
-неразложимые элементы исходной решётки. Тогда объект 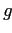 в
контексте будет обладать признаком
в
контексте будет обладать признаком 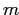 , если элемент решётки,
соответствующий
, если элемент решётки,
соответствующий 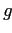 ,
находится "под" элементом, соответствующим
,
находится "под" элементом, соответствующим 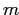 .
.
Определение 2.14
Строчно- (столбцево-)редуцированным называется такой
формальный контекст, в котором всякое объектное (признаковое)
понятие является
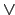
-неразложимым
(
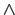
-неразложимым).
Редуцированным называется
формальный контекст, являющийся одновременно строчно- и
столбцево-редуцированным.
Определение 2.15
Пусть дан
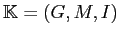
— формальный контекст и
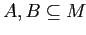
,
тогда
выражение
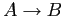
называется
импликацией (на множествах
признаков), если
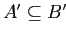
(или
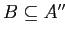
), т.е. все объекты из
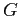
, обладающие
множеством признаков
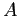
, обладают также множеством признаков
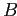
.
Аналогичным образом определяются импликации на множествах объектов.
Наличие импликации 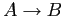 в контексте
в контексте
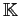 соответствует тому, что в
диаграмме решётки
соответствует тому, что в
диаграмме решётки
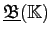 формальное понятие
формальное понятие
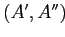 находится ниже формального понятия
находится ниже формального понятия
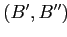 .
.
Импликации формального контекста удовлетворяют аксиомам
Армстронга [33] для произвольных 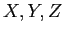 :
:
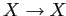 ;
;
- если
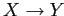 то
то
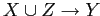 ;
;
- если
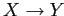 и
и
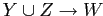 то
то
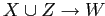 .
.
Помимо определённых выше однозначных (one-valued) формальных
контекстов в анализе формальных понятий изучаются многозначные
(many-valued) контексты:
Определение 2.16
Многозначный формальный контекст есть четвёрка
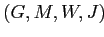
,
где
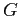
,
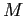
,
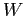
— множества (объектов,
признаков и значений признаков, соответственно), а
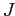
— тернарное
отношение
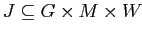
,
задающее значение
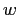
признака
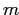
,
причём:
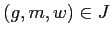
и
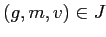
влечёт
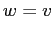
.
Многозначные признаки могут рассматриваться как отображения 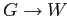 ,
таким образом, можно обозначать
,
таким образом, можно обозначать 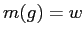 вместо
вместо
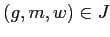 .
.
Процедура сведения многозначных контекстов к однозначным называется
шкалированием (scaling). Для шкалирования
каждый признак многозначного контекста представляется формальным
контекстом, называемым шкалой.
Определение 2.17
Шкала для признака
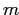
многозначного контекста
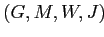
есть (однозначный) контекст
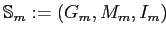
такой, что
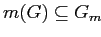
. Объекты в шкале называются
значениями
шкалы, а признаки —
признаками шкалы.
Определение 2.18
Пусть задан многозначный контекст
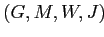
и шкалы
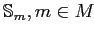
, тогда
производным контекстом будем называть контекст
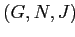
, где множество признаков
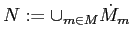
(
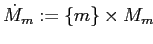
) и отношение
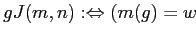
и
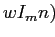
.
В нашей работе для построения таксономии алгоритмов использовалось два варианта шкалирования —
порядковое шкалирование и номинальное шкалирование. Порядковая шкала
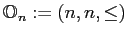 используется для признаков, значения которых упорядочены относительно
некоторого порядка
используется для признаков, значения которых упорядочены относительно
некоторого порядка 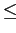 , а обладание объектом некоторым значением
признака влечёт обладание всеми меньшими значениями признака. С помощью номинальной шкалы
, а обладание объектом некоторым значением
признака влечёт обладание всеми меньшими значениями признака. С помощью номинальной шкалы
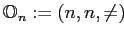 представляют несравнимые между собой значения признаков, например, цвет.
представляют несравнимые между собой значения признаков, например, цвет.
Возможные виды шкалирования рассмотрены в [33].
Назад Содержание Вперёд