2008 г.
Нечеткое сравнение коллекций: семантический и алгоритмический аспекты
Семенов В.А., Морозов С.В., Тарлапан О.А., Энкович И.В.
Труды Института системного программирования РАН
Работа коллектива поддержана РФФИ (грант 07-01-00427).
Назад Содержание Вперёд
3. Классификация коллекций
Коллекции — фундаментальный тип данных, поддерживаемый
популярными языками моделирования и программирования для спецификации и
реализации в приложениях агрегированных структурированных данных. Как
иллюстрируют примеры предыдущего раздела, сравнение коллекций должно проходить
в строгом соответствии с их семантикой. В противном случае результаты рискуют
быть неадекватными исходной проблеме и теряют смысл для целевого приложения и
пользователя.
Сравнение коллекций может рассматриваться в качестве частной
задачи более общей проблемы семантического сопоставления (matching) и сравнения (differencing) расходящихся реплик
структурированных данных, например, популяций объектов, заданных некоторой
объектно-ориентированной моделью. Несмотря на многообразие частных типов
коллекций, встречаемых в приложениях, можно выделить несколько фундаментальных
свойств, в соответствии с которыми их анализ может проводиться содержательным
образом. К таким свойствам мы относим уникальность элементов коллекции,
упорядочение, возможную сортировку элементов коллекции, а также ограниченный
размер коллекции.
Декларативные языки объектно-ориентированного моделирования,
как правило, предоставляют некоторый набор абстрактных или конкретных типов
коллекций с априори заданным набором семантических свойств. В производных
пользовательских типах, определяемых на основе базовых, семантика коллекций
может быть сохранена или уточнена. Однако выделенные фундаментальные свойства
остаются принципиальными для содержательного анализа коллекций.
Так,
декларативный язык ограничений OCL
[17] определяет абстрактный интерфейс коллекций Collection и четыре конкретных
класса Bag, Set, Sequence и OrderedSet для
представления мультимножеств, множеств, последовательностей и упорядоченных
множеств соответственно. Все виды коллекций задаются в обобщенном виде с
возможностью параметризации типом элементов. Set — коллекция, по семантике
соответствующая математическому понятию множества. Она не допускает дупликации
элементов. OrderedSet
— специализация данного типа для упорядоченных множеств. Ограничение
уникальности необходимо поддерживается данным типом коллекции. Bag
— мультимножество с возможным повторением элементов. Sequence — упорядоченное мультимножество или последовательность, допускающая
повторение элементов. Таким образом, виды коллекций OCL могут быть классифицированы в соответствии с таблицей 1.
Язык моделирования EXPRESS
[18] предоставляет иной набор типов коллекций, а именно: Aggregate, Bag, Set, Array
и List. Абстрактный тип Aggregate определяет базовый набор
методов оперирования с элементами коллекций. Bag — специализация данного
типа для представления мультимножеств. Set — специализация типа Aggregate для произвольных множеств, исключающая дупликацию элементов и
игнорирующая их порядок. Тип данных List применяется для
представления последовательностей. Допустимое количество элементов в списках, множествах и
мультимножествах задается дополнительными ограничениями. Коллекции имеют строго
фиксированный размер в тех случаях, когда нижний и верхний пределы их размера
совпадают. Array — специализация типа Aggregate для массивов фиксированной длины. С учетом индексации порядок элементов
в массивах имеет существенное значение. Возможна организация разреженных
массивов с неустановленными значениями элементов при помощи специального
спецификатора. Также возможно определение производных типов массивов и списков
с наложенным ограничением уникальности элементов. Базовые типы коллекций,
предоставляемые языком моделирования EXPRESS, приведены в таблице 1.
| UNIQUE |
ORDERED |
SORTED |
FIXED |
Используемые сокращения |
Коллекции OCL |
Коллекции EXPRESS |
| - |
- |
- |
- |
BAG |
BAG |
BAG |
| + |
- |
- |
- |
SET |
SET |
SET |
| - |
- |
- |
+ |
FIXED BAG |
|
|
| + |
- |
- |
+ |
FIXED SET |
|
|
| - |
+ |
- |
- |
LIST |
SEQUENCE |
LIST |
| + |
+ |
- |
- |
ORDERED SET |
ORDERED SET |
UNIQUE LIST |
| - |
+ |
- |
+ |
ARRAY |
|
ARRAY |
| + |
+ |
- |
+ |
UNIQUE ARRAY |
|
UNIQUE ARRAY |
| - |
+ |
+ |
- |
SORTED LIST |
|
|
| + |
+ |
+ |
- |
SORTED SET |
|
|
| - |
+ |
+ |
+ |
SORTED ARRAY |
|
|
| + |
+ |
+ |
+ |
SORTED UNIQUE ARRAY |
|
|
Таблица
1. Классификация базовых типов коллекций в языках моделирования EXPRESS и OCL
Базовые типы могут
переопределяться пользователем с учетом семантики приложения путем задания
дополнительных ограничений с использованием всего репертуара конструкций
декларативных языков OCL
и EXPRESS. В частности, может
быть уточнено допустимое число элементов коллекции и способ их индексации, задан
частичный или полный порядок на множестве элементов коллекции, определены
свойства корреляции значений элементов и т.п.
Рассмотрим
вопросы представления, вычисления изменений и исполнения соответствующих
операций над коллекциями, следуя приведенной выше классификации в соответствии
с выделенными семантическими свойствами.
4. Сравнение множеств
Начнем рассмотрение с наиболее простого типа коллекций 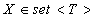 — множества
элементов типа T,
предполагающего неявное задание и выполнение единственного семантического
ограничения уникальности элементов
— множества
элементов типа T,
предполагающего неявное задание и выполнение единственного семантического
ограничения уникальности элементов 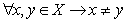 . Дельта для двух версий множества
. Дельта для двух версий множества 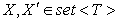 может быть
естественным образом представлена в виде неупорядоченного набора операций
добавления и удаления соответствующих элементов коллекции:
может быть
естественным образом представлена в виде неупорядоченного набора операций
добавления и удаления соответствующих элементов коллекции:
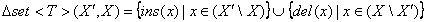
Корректное представление дельты 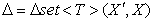 предполагает,
что выполняется условие
предполагает,
что выполняется условие 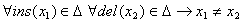 , означающее, что один и тот же элемент не может
одновременно участвовать в операции добавления и удаления. Более того, будем
исключать повторение операций добавления и удаления с одним и тем же элементом,
которое при исполнении операций противоречило бы определению множества:
, означающее, что один и тот же элемент не может
одновременно участвовать в операции добавления и удаления. Более того, будем
исключать повторение операций добавления и удаления с одним и тем же элементом,
которое при исполнении операций противоречило бы определению множества: 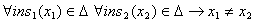 и
и 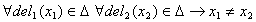 .
.
Применение операций, определяемых дельтой, довольно
прозрачно. К заданному исходному множеству добавляются элементы, определяемые
операциями ins,
и удаляются элементы, определяемые операциями del. Тем самым, гарантируется
тождественность условия 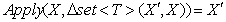 , в котором функция
, в котором функция 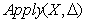 возвращает
модифицированное представление коллекции, полученное в результате применения дельты к заданному
представлению коллекции X.
возвращает
модифицированное представление коллекции, полученное в результате применения дельты к заданному
представлению коллекции X.
Две конкурентные транзакции 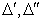 могут оказаться
конфликтными в случае
могут оказаться
конфликтными в случае 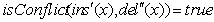 , когда в одной транзакции некоторый элемент
добавляется в коллекцию, а в другой транзакции тот же самый элемент удаляется.
Однако, если обе дельты вычислялись относительно общей версии коллекции в
рамках распространенной схемы слияния “3-way Merge”:
, когда в одной транзакции некоторый элемент
добавляется в коллекцию, а в другой транзакции тот же самый элемент удаляется.
Однако, если обе дельты вычислялись относительно общей версии коллекции в
рамках распространенной схемы слияния “3-way Merge”: 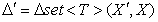 ,
, 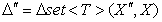 , то подобные конфликты исключены в силу того, что
удаляемый элемент обязан принадлежать базовой версии коллекции X и не может быть
добавлен в нее повторно вследствие ограничения уникальности элементов
множества. В случае иных схем слияния с участием нескольких базовых версий,
например, схемы “4-way Merge”,
подобные конфликты должны идентифицироваться и корректно разрешаться.
Тривиальными способами разрешения являются следующие опции
, то подобные конфликты исключены в силу того, что
удаляемый элемент обязан принадлежать базовой версии коллекции X и не может быть
добавлен в нее повторно вследствие ограничения уникальности элементов
множества. В случае иных схем слияния с участием нескольких базовых версий,
например, схемы “4-way Merge”,
подобные конфликты должны идентифицироваться и корректно разрешаться.
Тривиальными способами разрешения являются следующие опции 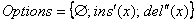 , предполагающие игнорирование обеих конфликтных
операций или принятие одной из них.
, предполагающие игнорирование обеих конфликтных
операций или принятие одной из них.
Сложность вычисления дельты 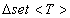 определяется,
прежде всего, способом представления исходных множеств (список, массив, сбалансированное
дерево), а также алгоритмами поиска добавляемых и удаляемых элементов.
Вычислительная сложность наивной реализации, основанной на простом поиске
элемента в неупорядоченном списке и не требующей определения на элементах
множеств полного порядка может быть оценена как
определяется,
прежде всего, способом представления исходных множеств (список, массив, сбалансированное
дерево), а также алгоритмами поиска добавляемых и удаляемых элементов.
Вычислительная сложность наивной реализации, основанной на простом поиске
элемента в неупорядоченном списке и не требующей определения на элементах
множеств полного порядка может быть оценена как 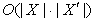 . Сложность оптимальной реализации, основанной на
предварительной сортировке исходных множеств, например, методом пирамидальной
сортировки или методом слияния списков, можно оценить как
. Сложность оптимальной реализации, основанной на
предварительной сортировке исходных множеств, например, методом пирамидальной
сортировки или методом слияния списков, можно оценить как 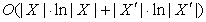 . А в случае использования для работы с множеством
сбалансированного дерева, хранящего элементы в уже отсортированном порядке,
сложность операции построения дельты оценивается как
. А в случае использования для работы с множеством
сбалансированного дерева, хранящего элементы в уже отсортированном порядке,
сложность операции построения дельты оценивается как 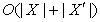 . Понятно, что последняя оценка не может
рассматриваться как реальная оценка, поскольку в данном случае основная часть
затрат перенесена на стадию формирования исходных множеств. Наиболее корректной
оценкой в данном случае является также
. Понятно, что последняя оценка не может
рассматриваться как реальная оценка, поскольку в данном случае основная часть
затрат перенесена на стадию формирования исходных множеств. Наиболее корректной
оценкой в данном случае является также 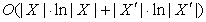 .
.
Ниже приведен пример сравнения двух версий множества
натуральных чисел 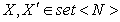 . Пусть
. Пусть 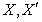 — основная и
модифицированная версии коллекции, содержащие следующие элементы:
— основная и
модифицированная версии коллекции, содержащие следующие элементы:  ,
, 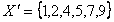 . Тогда дельта, вычисленная путем сравнения двух версий
множества, представляется как
. Тогда дельта, вычисленная путем сравнения двух версий
множества, представляется как 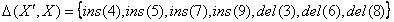 .
.
5. Сравнение мультимножеств
Перейдем к задаче сравнения мультимножеств 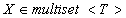 с функцией
с функцией 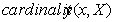 для подсчета
числа вхождений элемента
для подсчета
числа вхождений элемента 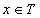 в коллекцию
в коллекцию 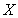 . При модификации коллекции данного типа дельта
представляется как неупорядоченный набор множественного добавления и удаления
элементов. Пусть
. При модификации коллекции данного типа дельта
представляется как неупорядоченный набор множественного добавления и удаления
элементов. Пусть 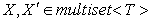 — две версии
мультимножества, тогда дельта может быть сформирована как
— две версии
мультимножества, тогда дельта может быть сформирована как
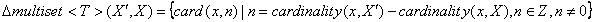
В используемых обозначениях Z — множество целых чисел.
Положительное значение параметра n в операции изменения кардинальности card(x,n) указывает на добавление элемента
в коллекцию соответствующее число раз, отрицательное значение — на удаление
элемента из коллекции. Нулевое значение n не содержательно для представления дельты, поскольку
означает, что количество экземпляров элемента в коллекции не изменилось. В
корректно сформированном представлении дельты 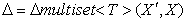 предполагается,
что элемент мультимножества не может одновременно участвовать в нескольких
операциях
предполагается,
что элемент мультимножества не может одновременно участвовать в нескольких
операциях 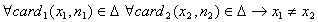 . В противном случае сравнение идентичных версий
коллекции могло бы привести к неожиданному результату, отличному от пустого
представления дельты, например:
. В противном случае сравнение идентичных версий
коллекции могло бы привести к неожиданному результату, отличному от пустого
представления дельты, например: 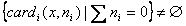 .
.
Применение базовой операции дельты card(x,n) состоит в кратном добавлении
соответствующего элемента x
при положительном значении параметра n и в его кратном удалении при отрицательном значении параметра.
Это гарантирует выполнение необходимого тождества 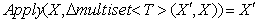 .
.
Две операции 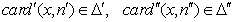 конфликтуют
друг с другом, если параметры кратности перемещения экземпляров одного и того
же элемента в конкурентных транзакциях отличаются друг от друга
конфликтуют
друг с другом, если параметры кратности перемещения экземпляров одного и того
же элемента в конкурентных транзакциях отличаются друг от друга 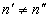 . Тривиальные способы разрешения конфликта состоят в
выборе одной из опций
. Тривиальные способы разрешения конфликта состоят в
выборе одной из опций 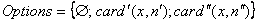 . Вместе с тем, логичным представляется расширение
возможных опций путем назначения параметру кратности всего интервала значений,
порождающего конфликтную ситуацию:
. Вместе с тем, логичным представляется расширение
возможных опций путем назначения параметру кратности всего интервала значений,
порождающего конфликтную ситуацию: 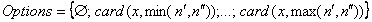 . Это означает, что может быть выбрано любое число
кратности для операции перемещения, лежащее в интервале между соответствующими
параметрами конфликтных операций. В случаях, когда обе конфликтные операции
являются родственными, конфликт целесообразно разрешать, исходя из
промежуточных значений. В случаях, когда одна из конфликтных операций —
операция добавления, а другая — операция удаления, допустимым является также
весь диапазон значений параметра кратности, означая удаление или добавление
числа элементов, не превышающего используемое значение соответствующей
операции.
. Это означает, что может быть выбрано любое число
кратности для операции перемещения, лежащее в интервале между соответствующими
параметрами конфликтных операций. В случаях, когда обе конфликтные операции
являются родственными, конфликт целесообразно разрешать, исходя из
промежуточных значений. В случаях, когда одна из конфликтных операций —
операция добавления, а другая — операция удаления, допустимым является также
весь диапазон значений параметра кратности, означая удаление или добавление
числа элементов, не превышающего используемое значение соответствующей
операции.
Сложность построения 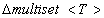 определяется
теми же факторами, что и сложность вычисления дельты обычного множества. Имеет
место незначительное увеличение числа операций, однако это не влияет на
асимптотическую оценку, которая в среднем выражается как
определяется
теми же факторами, что и сложность вычисления дельты обычного множества. Имеет
место незначительное увеличение числа операций, однако это не влияет на
асимптотическую оценку, которая в среднем выражается как 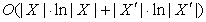 .
.
В качестве примера рассмотрим процедуру сравнения двух
версий мультимножества символов. Пусть 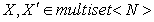 — основная и
модифицированная версии коллекции, содержащие следующие натуральные элементы
— основная и
модифицированная версии коллекции, содержащие следующие натуральные элементы 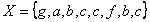 ,
, 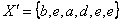 . Тогда дельта, вычисленная в результате сравнения
двух версий коллекции, представляется как
. Тогда дельта, вычисленная в результате сравнения
двух версий коллекции, представляется как
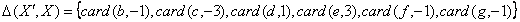 .
.
Назад Содержание Вперёд